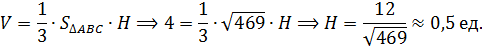Смешанное произведение векторов и его свойства
Определение. Смешанным произведением трёх векторов (обозначается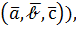 
называется скалярное произведение вектора 
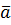на векторное произведение 
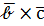, т.е.
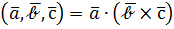(17)
Из формулы (17) следует, что свойства смешанного произведения являются следствиями свойств скалярного и векторного произведений векторов. Перечислим их без доказательств.
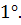Смешанное произведение не меняется при круговой перестановке сомножителей:
Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объёму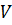 
параллелепипеда, построенного на векторах:
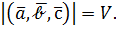
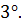Из свойства 
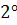следует, что если векторы 
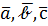лежат в одной плоскости (параллельны одной плоскости, т.е. компланарны), то параллелепипеда на них построить нельзя (его объём равен нулю) и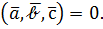 
Таким образом, равенство нулю смешанного произведения есть условие компланарности трёх векторов.
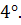Смешанное произведение в координатной форме. Пусть
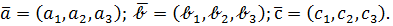Тогда
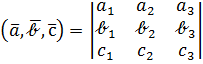(18)
Например, пусть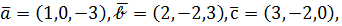 
тогда
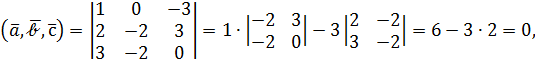
т.е. эти три вектора параллельны одной плоскости (компланарны).
Пример 6. Даны три не компланарных вектора 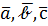. Выяснить, компланарны ли векторы 
, 
, 
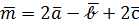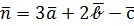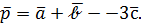
Решение. Векторы заданы в бескоординатной форме, поэтому пользуемся определением и правилами оперирования как с многочленами:
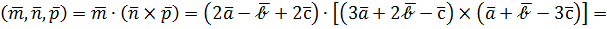
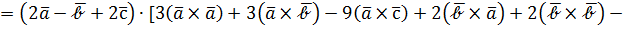
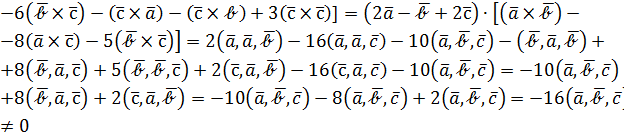, т.к. 
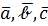- некомпланарны.
Ответ: Векторы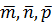 
некомпланарны.
Подводя итог и имея в виду геометрические приложения, запомним, что для вычисления углов и длин используем скалярное произведение; для вычисления площадей - векторное произведение; для вычисления объёмов – смешанное произведение.
Пример 7. Даны координаты вершин пирамиды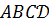 
. Найти: 1) угол между ребрам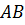и 
и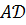 
; 2) площадь грани 
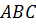; 3) проекцию вектора 
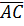на вектор 
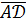; 4) объём пирамиды 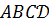; 5) длину высоты пирамиды, проведённой из точки 
. 
.
|
|
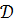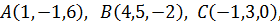
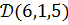Введём векторы 
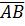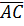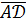, и и 
вычислим их координаты, вычитая
из координат конца координаты начала:
|
|
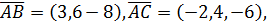
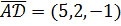. 1) Угол между рёбрам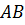и и 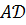найдём как угол между векторам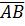и и 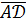с помощью скалярного произведения:
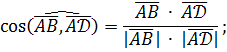
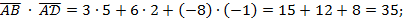
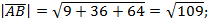
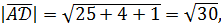следовательно
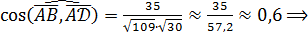по таблицам находим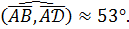 
2) Площадь грани 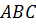вычислим с помощью векторного произведения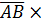 
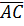, точнее, с помощью его модуля: 
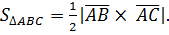Сначала найдём само векторное произведение: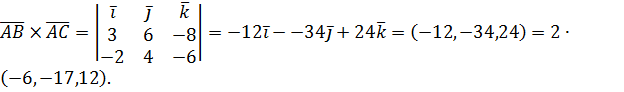 
Тогда
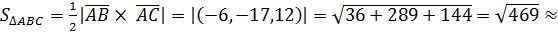21,6 ед.2
3) Проекцию вектора 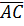на вектор 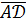находим с помощью скалярного произведения:
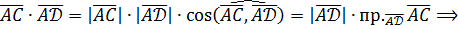
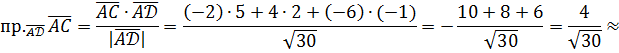
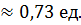
4) Объём 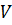пирамиды 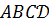равен 
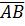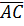объёма параллелепипеда, построенного на векторах , и 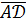, который равен модулю их смешанного произведения. Поэтому сначала находим смешанное произведение:
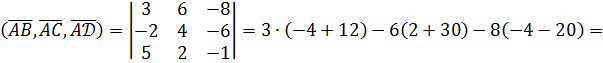
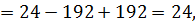следовательно,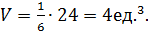 
5) Объём пирамиды равен произведению 
площади основания на высоту:
