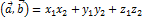Теорема о существовании обратной матрицы
Пусть А (mxn), B(p,q). При каких условиях на m,n,p,q существуют произведения этих матриц?
Произведением матриц 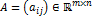 и
и 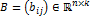 называется матрица
называется матрица 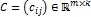 , элементы которой определены равенством
, элементы которой определены равенством
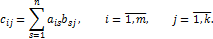
Произведение матриц 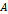 и
и 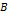 будем обозначать
будем обозначать 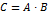 .
.
Из определения следует, что произведение 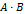 определено лишь в том случае, когда число столбцов матрицы
определено лишь в том случае, когда число столбцов матрицы 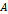 совпадает с числом строк матрицы
совпадает с числом строк матрицы 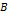 . Это означает, что оба произведения
. Это означает, что оба произведения 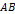 и
и 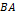 определены тогда и только тогда, когда матрицы A и B имеют размеры
определены тогда и только тогда, когда матрицы A и B имеют размеры 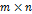 и
и 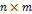 соответственно. Следовательно равенство
соответственно. Следовательно равенство 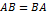 возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.
возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.
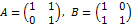 , тогда
, тогда
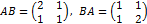 .
.
Следовательно 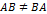 .
.
Может ли произведение 2х ненулевых матриц равняться нулевой?
Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что А ∙ В =0, не следует, что А=0, или B=0. Например,
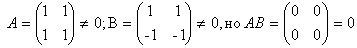
Ф-лы сокращенного умножения для матриц.
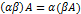
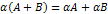 (Распределительное свойство относительно сложения матриц);
(Распределительное свойство относительно сложения матриц);
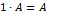
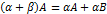 (Распределительное свойство относительно сложения чисел);
(Распределительное свойство относительно сложения чисел);
 .
.
Операция умножения матриц обладает следующими свойствами:
 (Свойство ассоциативности),
(Свойство ассоциативности),
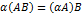 , для любого действительного числа α,
, для любого действительного числа α,
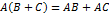 ,
, 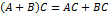 (Свойство дистрибутивности)
(Свойство дистрибутивности)
Определение линейно зависимых строк (столбцов) матрицы.
Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу)
Определение линейно независимых строк (столбцов) матрицы.
Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).
Ранг прямоугольной матрицы.
Ранг столбца (или строки) прямоугольной матрицы чисел равно числу линейно независимых столбцов (или строк) элементов матрицы. Если не существует зависимых столбцов, то ранг матрицы равен числу всех столбцов, и говорят, что матрица имеет полный ранг. Если ранг матрицы меньше числа столбцов, то говорят, что матрица имеет неполный ранг, и она называется вырожденной.
Сформулировать теорему Кронекера-Капелли.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы.
Формулы Крамера
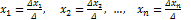
Ф-ла для обратной матрицы в общем виде.
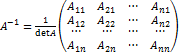
Теорема о существовании обратной матрицы.
Матрица 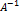 называется обратной к матрице
называется обратной к матрице 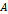 , если
, если 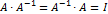 , где
, где 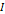 - единичная матрица. Матрица
- единичная матрица. Матрица 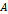 , для которой существует обратная матрица, называется обратимой.
, для которой существует обратная матрица, называется обратимой.
Так как равенство 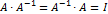 возможно лишь для квадратных матриц
возможно лишь для квадратных матриц 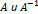 одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима.
одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима.
Критерий обратимости
Матрица 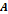 обратима тогда и только тогда, когда она не вырождена.
обратима тогда и только тогда, когда она не вырождена.
Квадратная матрица 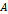 называется вырожденной, если
называется вырожденной, если 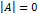 , и невырожденной, если
, и невырожденной, если 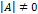 .
.
12. Сформулировать условие сеществования и единственности решения СЛАУ:Система линейных алгебраических уравнений с квадратной невырожденной матрицей совместна и имеет единственное решение.
13. Сформулировать теорему об определителях треугольной и диагональной матриц:Определитель любой верхней треугольной (нижней треугольной) матрицы равен произведению диагональных элементов. Определитель любой диагональной матрицы равен произведению диагональных элементов.
14. Сформулировать теорему об определителе произведения матриц:Определитель произведения квадратных матриц 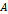 и
и 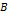 равен произведению определителей матриц-сомножителей, т.е.
равен произведению определителей матриц-сомножителей, т.е. 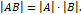
15. Определить операции с векторами (сумма, разность, произведение вектора на число) и указать их свойства:Суммой двух векторов 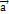 и
и 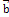 называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора 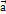 в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора 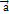 Правило сложения векторов обладает следующими свойствами:1.
Правило сложения векторов обладает следующими свойствами:1. 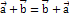 (Коммутативностьсложения)2.
(Коммутативностьсложения)2. 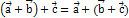 (Ассоциативность сложения)3.Существует нулевой вектор
(Ассоциативность сложения)3.Существует нулевой вектор 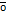 , такой что
, такой что 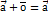 для любого вектора
для любого вектора 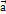 . 4.Для любого вектора
. 4.Для любого вектора 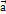 существует противоположный к нему вектор
существует противоположный к нему вектор 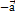 , такой, что
, такой, что 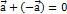 . Разностью векторов
. Разностью векторов 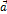 и
и  называется такой вектор
называется такой вектор 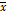 , что
, что 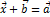 . Произведением
. Произведением 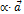 вектора
вектора 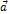 на число
на число 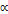 называется вектор
называется вектор 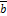 , коллинеарный вектору
, коллинеарный вектору 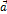 , имеющий длину
, имеющий длину 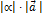 и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора 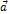 в случае
в случае 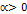 и противоположное направлению
и противоположное направлению 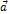 в случае
в случае 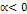 . В случае, когда
. В случае, когда 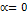 , или
, или 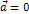 произведение
произведение 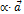 представляет собой нулевой вектор, направление которого не определено. Операция умножения вектора на число обладает следующими свойствами:
представляет собой нулевой вектор, направление которого не определено. Операция умножения вектора на число обладает следующими свойствами: 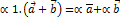 ; 2.
; 2. 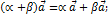 3.
3. 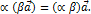
16. Дать инвариантное определение скалярного произведения двух векторов:Скалярным произведением двух ненулевых векторов 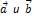 называется число, равное произведению длин этих векторов на косинус угла 𝜑 между ними.
называется число, равное произведению длин этих векторов на косинус угла 𝜑 между ними.
17. Написать формулу для вычисления скалярного произведения двух векторов в декартовой С.К.: