Метод обратной матрицы и теорема Крамера

В этом разделе мы рассмотрим частный случай системы (15.1), когда число уравнений равно числу неизвестных, т.е. т = n. Система уравнений имеет вид

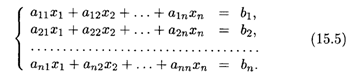
Составим квадратную матрицу А порядка n этой системы:

1. В матричной форме система уравнений (15.5) имеет вид

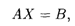
где матрицы Х и В имеют размер n х 1. Пусть матрица систе­мы А является невырожденной, т.е. существует обратная мат­рица А^-1. Умножив обе части этого уравнения слева на А^-1, получаем решение системы (15.5) в матричной форме:

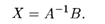
Вычисление обратной матрицы по заданной матрице А производится по довольно сложным формулам. В случае когда по­рядок n матриц А и А^-1 достаточно велик, вычисление обрат­ной матрицы может быть очень громоздким.

2. Другой метод решения системы уравнений (15.5) основан на теореме Крамера. Составим определитель матрицы систе­мы А:

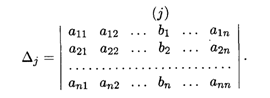
который называется также определителем системы. Заменим в этом определителе j-й столбец на столбец свободных членов В, т.е. получим этой заменой другой определитель, который обозначим Δ_j:

ТЕОРЕМА 2 (правило Крамера). Пусть Δ — определитель матрицы системы А, а Δ_j — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов В. Тогда если Δ ≠ 0, то система линейных уравнений (15.5) имеет единственное решение, определяемое по форму­лам

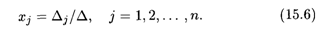
Формулы вычисления неизвестных (15.6) — решения сис­темы (15.5) — носят название формул Крамера.

Пример 1. Найти решение системы уравнений

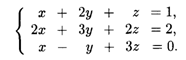
Решение. Составим и вычислим определители системы Δ и Δ_j (j = x, y, z):

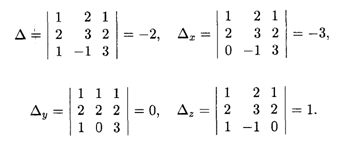
Определитель системы отличен от нуля, стало быть, она имеет единственное решение, которое вычисляется по форму­лам (15.6):

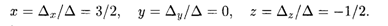
Решение системы общего вида

Пусть задана система линейных уравнений общего вида (15.1), где т ≤ n, т.е. число неизвестных не меньше числа уравнений. Представим общий порядок решения этой системы.

1. Необходимо определить совместность системы, т.е. опре­делить сначала ранги матрицы системы А и расширенной мат­рицы A_B. По теореме Кронекера-Капелли если ранги этих матриц не совпадают, то система несовместна и тогда нет смысла ее решать. Если же ранги матриц А и А_B равны, то система (15.1) совместна.

Определение 1. Рангом совместной системы линейных алгеб­раических уравнений называется ранг ее матрицы.

2. Пусть система (15.1) совместна и ранг ее равен r. Вы­делим в матрице системы (15.2) некоторый базисный минор; предположим, что именно первые r строк матриц А и А_B яв­ляются базисными. Тогда по теореме о базисном миноре ос­тальные строки матрицы являются линейными комбинациями остальных строк. В свою очередь это означает, что в системе (15.1) первые r уравнений, соответствующие базисным стро­кам матрицы А, являются базисными, а остальные — их ли­нейными комбинациями. Тогда эти (m — r) уравнений можно удалить из системы, причем в результате указанных элемен­тарных преобразований мы получаем эквивалентную систему:

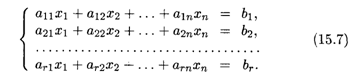
3. Система (15.7) характерна тем, что ее ранг равен числу уравнений в ней, причем r ≤ n, т.е. ранг не превосходит числа неизвестных. Поэтому возможны два случая: либо r = n, либо r < n. В первом случае система (15.7) имеет квадратную невырожденную матрицу порядка r (см. выше) и, согласно теореме Крамера, существует единственное решение этой системы. Иными словами, если ранг системы равен числу неизвестных, то система имеет единственное решение, т.е. она является оп­ределенной.

4. Рассмотрим теперь случай, когда r < п. Перенесем в правые части уравнений (15.7) все слагаемые, содержащие не­известные x_r+1, x_r+2, …, x_п. Тогда система принимает вид

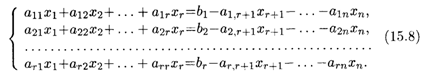
Неизвестным x_r+1, ..., x_п можно придавать любые значения, и потому они называются свободными. Неизвестные х₁, x₂, ..., x_r соответствующие базисным столбцам, называются базисными. Из системы (15.8) легко найти выражения базисных неизвест­ных через свободные, согласно теореме Крамера, рассматри­вая правые части этих уравнений как элементы столбца сво­бодных членов, содержащие x_r+1, x_r+2,…, х_п. Можно показать, что базисные неизвестные x₁, х₂, ..., x_r линейно выражаются через свободные неизвестные. Поскольку свободные неизвест­ные могут принимать любые значения, то в случае когда ранг совместной системы меньше числа неизвестных, эта система является неопределенной: она имеет бесчисленное множество решений.

Метод Гаусса

Следует заметить, что как метод обратной матрицы, так и метод Крамера являются очень трудоемкими по количест­ву вычислительной работы. Оба они требуют порядка n²n! арифметических действий для нахождения решения системы линейных уравнений. При п = 5 это составит около 3000 дей­ствий, при п = 10 — около 3,6 ∙ 10⁸ действий. При решении серьезных задач приходится иметь дело с системами уравне­ний порядка п = 100 и более. При таких масштабах даже су­перкомпьютерам потребуется огромное время для вычисления решения. Кроме того, погрешности компьютерного округления чисел приводят к значительным ошибкам в расчетах численно­го решения систем уравнений большого порядка. Между тем существуют более экономичные методы решения систем ли­нейных уравнений, основанные на предварительном преобра­зовании расширенной матрицы системы к специальному виду. В частности, одним из них является метод Гаусса, практичес­кую реализацию которого мы приводим ниже.

Рассмотрим систему уравнений общего вида (15.1). Пусть для определенности a₁₁ ≠ 0 (если a₁₁ = 0, то можно переста­вить на первое место ненулевое слагаемое или начать с другого уравнения). Умножим первое уравнение системы (15.1) на чис­ло a₂₁/a₁₁ и затем вычтем его из второго уравнения этой системы. Умножим обе части первого уравнения на число a₃₁/a₁₁ и затем вычтем его из третьего уравнения и так далее, т.е. процесс заключается в последовательном вычитании первого уравнения, умножаемого на числа a_i1/a₁₁, из i-го уравнения (i = 2, 3, ... , m). Таким образом, в результате элементарных преобразований мы получим эквивалентную систему, в кото­рой начиная со второго уравнения отсутствуют слагаемые, со­держащие неизвестное x₁:

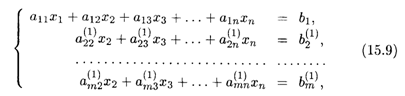
где верхний индекс в скобках означает новые коэффициенты, полученные после первого шага. Для удобства записи будем оперировать расширенной матрицей системы, отделяя в ней вертикальной чертой столбец свободных членов. Итак, после первого шага, содержащего (т — 1) элементарных преобразо­ваний системы, мы переходим от расширенной матрицы (15.4) исходной системы к расширенной матрице

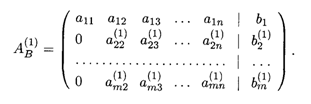
Второй шаг заключается в том, что теперь второе уравне­ние системы (15.7) или вторая строка матрицы (15.8) исполь­зуется для аналогичных элементарных преобразований строк с третьей по m-ю: эта строка последовательно умножается на число 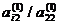и вычитается из i-й строки (i = 3, 4, ... ,m). В результате этих (m - 2) элементарных преобразований полу­чаем новую расширенную матрицу, соответствующую новой эквивалентной системе уравнений. Эта матрица имеет вид

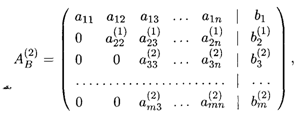
где верхний индекс означает новые коэффициенты. В случае если элемент 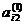= 0, то второе уравнение можно поменять местами с другим уравнением, у которого элемент 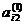≠ 0.

Продолжим этот процесс аналогичным образом (т.е. на 3-м шаге преобразуются строки с 4-й по т-ю, на 4-м шаге — стро­ки с 5-й по m-ю и т.д.) до тех пор, пока не дойдем до последней m-й строки. После (r - 1)-го шага процесса последовательного исключения неизвестных мы получим следующую расширен­ную матрицу:

Последние (m - r) строк этой матрицы соответствуют урав­нениям эквивалентной системы уравнений

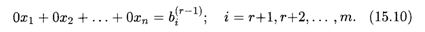
Эти уравнения могут появиться, если соответствующие урав­нения исходной системы (15.1) представляют собой линейные комбинации других уравнений этой системы, о чем говорилось в п. 15.1. Здесь мы не исследовали заранее систему (15.1) на совместность; поэтому если эта система несовместна, то хотя бы одно из чисел 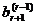, ,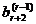..., 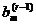не равно нулю. Таким образом, метод Гаусса позволяет на определенном шаге устано­вить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся ли­нейными комбинациями других уравнений системы (15.1), если она совместна.

Пусть система (15.1) совместна, тогда все правые части уравнений (15.10) равны нулю, и после удаления нулевых урав­нений в эквивалентной системе и нулевых строк в расширенной матрице получаем матрицу специфического ступенчатого ви­да, ранг которой равен r. Все элементы этой матрицы, стоящие слева или ниже элементов а_ij, равны нулю:

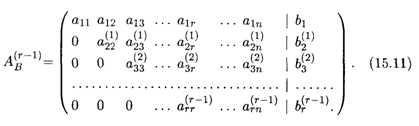
Эта расширенная матрица соответствует системе уравнений ранга r, которая имеет вид

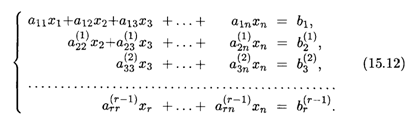
Система уравнений (15.12) уже полностью подготовлена к на­хождению решения, процесс которого осуществляется снизу вверх, т.е. от последнего уравнения к первому. Переход от сис­темы (15.1) к эквивалентной ей системе (15.12) называется пря­мым ходом, а нахождение неизвестных из системы (15.12) — обратным ходом метода Гаусса. Далее последовательность действий аналогична изложенной выше.

1. Если r = n, то система (15.12) имеет вид

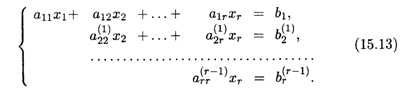
Поднимаясь снизу вверх, последовательно находим (обратный ход метода Гаусса):

— из последнего r-го уравнения неизвестное x_r = ;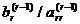

— из (r - 1)-го уравнения неизвестное x_r-1 путем подста­новки в это уравнение уже найденного неизвестного x_r;

— из i-го уравнения неизвестное x_i при подстановке в него найденных величин x_r, x_r-1, ..., x_i-1;

— и так далее до первого уравнения, из которого при под­становке в него уже найденных величин x_r, x_r-1 , ..., x₂ находим х₁.

2. Ранг системы уравнений (15.12) меньше n. В этом слу­чае, как и ранее, объявляем неизвестные x_r+1, x_r+2, …, x_п, сво­бодными и формируем правые части уравнений (15.12), остав­ляя в левых частях слагаемые, содержащие базисные перемен­ные x₁, x₂, ..., x_r:

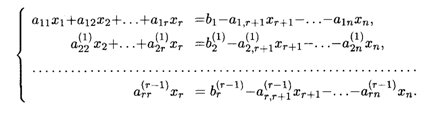
Решение этой системы находится обратным ходом метода; те­перь базисные неизвестные зависят от свободных неизвестных, которые могут принимать любые значения, а потому система (15.1) имеет бесчисленное множество решений.

Рассмотрим примеры решения систем линейных уравнений методом Гаусса.

Пример 2. Пример 1 п. 15.2.

Решение. Выпишем расширенную матрицу этой системы; справа в скобках укажем числа, на которые умножается соот­ветствующая строка матрицы для того, чтобы сложить ее с нижними строками. Горизонтальными стрелками показаны пе­реходы к расширенным матрицам эквивалентных систем. Пер­вую строку расширенной матрицы исходной системы умножа­ем последовательно на (-2) и (-1) и прибавляем ее соответ­ственно к 2-й и 3-й строкам этой матрицы. После первого шага, состоящего в "обнулении" первого столбца согласно формуле (15.9), получаем (номера шагов показаны перед стрелками пе­рехода)

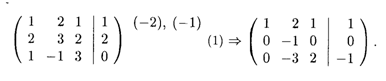
Второй шаг прямого хода метода Гаусса состоит в операциях с преобразованной расширенной матрицей: прибавляем вторую строку, умноженную на (-3), к 3-й строке:

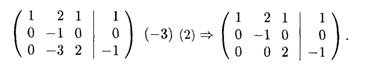
Последний вид расширенной матрицы является конечным эта­пом прямого хода метода (см. формулу (15.13)), после чего при­ступаем к обратному ходу, т.е. находим неизвестные, начиная с последнего. Полученная расширенная матрица соответствует системе уравнений

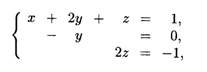
которая эквивалентна исходной системе. Отсюда последова­тельно находим: z = -1/2, у = 0,х = 1- 0 - (-1/2) = 3/2.

Пример 3. Решить методом Гаусса систему линейных уравнений

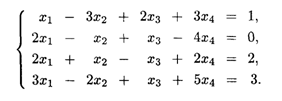
Решение. Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода ме­тода Гаусса. Имеем

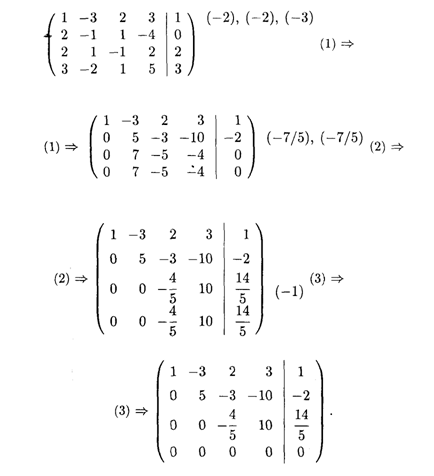
Последняя нулевая строка в расширенной матрице, полученной после 3-го шага, появилась из-за того, что в исходной системе четвертое уравнение является суммой 1-го и 3-го уравнений. Система совместная, и после удаления нулевой строки заклю­чительный вид расширенной матрицы соответствует системе трех уравнений с четырьмя неизвестными (ранг системы мень­ше числа неизвестных). Полагая x₄ свободной переменной, по­лучаем

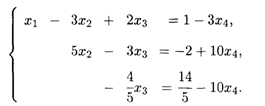
Из этой системы обратным ходом метода Гаусса находим

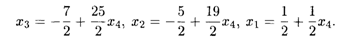
Данная система уравнений имеет бесчисленное множество ре­шений, поскольку x₄ может принимать любые значения.