Прямоугольная система координат в пространстве

Многие характеристики окружающих нас явлений описываются числами, например температура тела, вес и стоимость товара, плотность, масса, валентность, объем, количество участников конференции. Такие величины называются скалярными, или просто скалярами. Однако имеются величины, которые для своего описания требуют еще и указание направления, например скорость, сила, ускорение. Такие величины называются векторными, или просто векторами.

ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ

Прямоугольная система координат 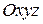в пространстве определяется заданием масштабной единицы измерения длин и трех пересекающихся в одной точке О взаимно перпендикулярных осей: 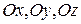. Точка О – начало координат, 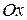– ось абсцисс, 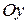– ось ординат, 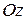– ось аппликат. Пусть М – произвольная точка пространства. Прямоугольными координатами точки М называются числа 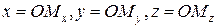, то есть величины направленных отрезков 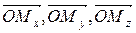; при этом 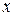называется абсциссой, 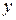- ординатой, 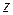- аппликатой точки М. Таким образом, при выбранной системе координат каждой точке М пространства соответствует единственная упорядоченная тройка чисел (x,y,z) – ее прямоугольные координаты и обратно, каждой упорядоченной тройке чисел (x,y,z) соответствует, и при том только одна, точка М пространства. Плоскости 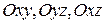называются координатными плоскостями. Они делят все пространство на восемь частей, называемых октантами.

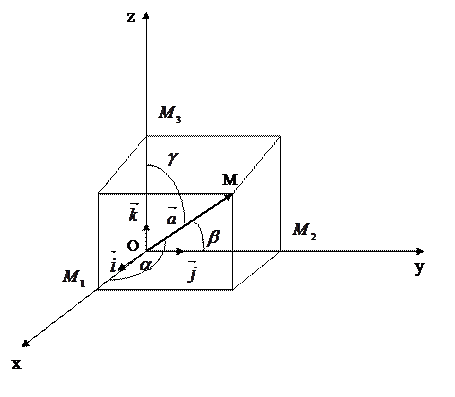Рис. 1 .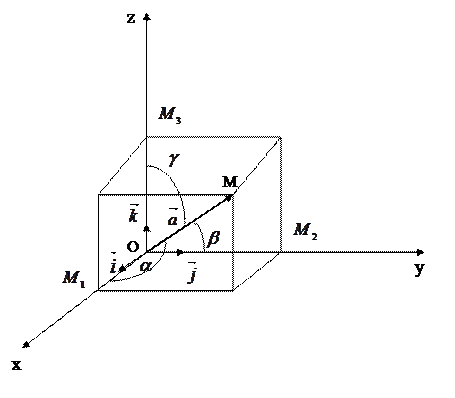

2. ПОНЯТИЕ ВЕКТОРА

Вектором называется направленный отрезок, на котором заданы начало, конец и направление, то есть упорядоченная пара точек А и В пространства определяет вектор 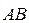. При этом первая буква означает начало вектора, а вторая – его конец. Вектор обозначают и одной прописной буквой .

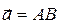Длиной (модулем) вектора называется расстояние между началом и концом вектора .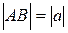

Пусть заданы координаты точек–концов вектора 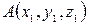, , 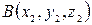тогда координаты вектора получим, вычитая из координат конца 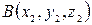координаты начала :

.

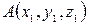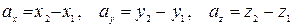Длина вектора 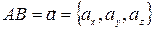равна квадратному корню из суммы квадратов его координат

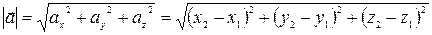(1)

Вектор, у которого начало и конец совпадают, называется нулевым и обозначается , .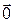

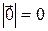Вектор, длина которого равна единице, называется единичным вектором и обозначается через 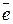. Единичный вектор, направление которого совпадает с направлением вектора 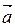, называется ортом вектора 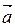и обозначается 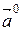, в частности, единичные вектора, совпадающие по направлениям с координатными осями, обозначают .

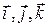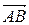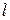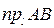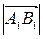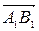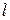Проекцией вектора на ось называется положительное число = , если вектор и ось одинаково направлены и отрицательное число 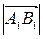, если вектор 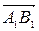и ось 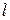противоположно направлены.

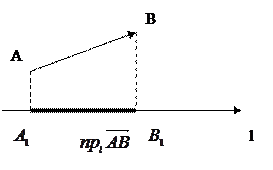Рис. 2.

Основные свойства проекций.

1) 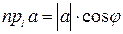, где 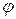- угол между вектором 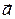и осью ;

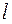2)

.

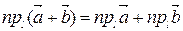
Из рис. 1 видно, что

; ;

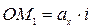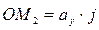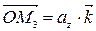
и -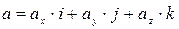

формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.

Углы вектора 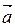с осями 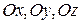соответственно равны .

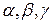Направляющие косинусы вектора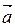

, , .

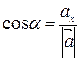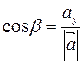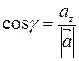(2)

Сумма квадратов направляющих косинусов ненулевого вектора равна единице: .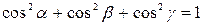

Пример 1. Вычислить длину и направляющие косинусы вектора 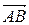, если даны координаты точек 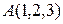и .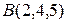

Решение. Найдем координаты вектора .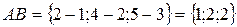

Длина вектора по (1) 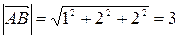.