Основные тригонометрические формулы
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
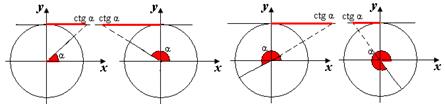
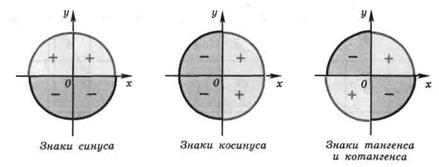
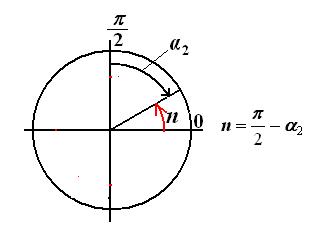
Тригонометрический круг
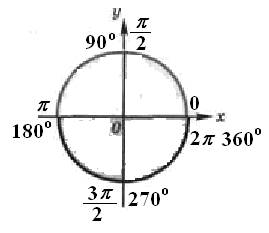
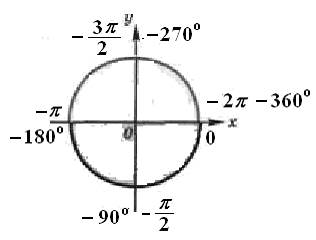
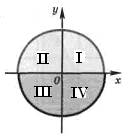
1.Углом какой четверти является угол α, если:
а) α = 283˚ б) α = 190˚
в) α = 100˚ г) α = –20˚
д) α = –110˚ е) α = 4200˚
ж)α = 179˚ з) α = 325˚
и) α = –150˚ к) α = –10˚
л) α = 800˚ м) α = 10 000˚
| а | 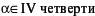 | б | 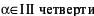 |
| в | 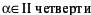 | г | 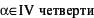 |
| д | 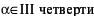 | е | 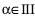 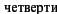 |
| ж | 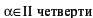 | з | 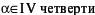 |
| и | 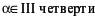 | к | 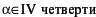 |
| л | 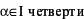 | м | 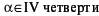 |
Радианная мера угла
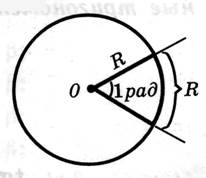
180˚ = π рад
Преобразование углов из градусной меры в радианную:
α рад = 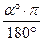
Преобразование углов из радианной меры в градусную:
α˚ = 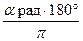
2. Выразите в радианной мере величины углов:
а) 45˚, 36˚, 180˚; б) 120˚, 310˚, 360˚;
в) 60˚, 72˚, 270˚; г) 150˚, 216˚, 90˚.
| а | 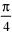 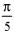 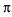 | б | 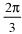 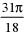 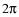 |
| в | 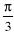 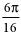 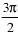 | г | 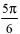 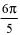 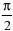 |
3. Выразите в градусной мере величины углов:
а) 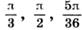 ; б)
; б) 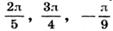 ;
;
в) 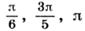 ; г)
; г) 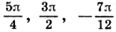
| а | 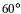 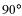 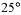 | б | 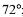 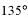 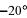 |
| в | 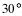 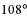 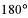 | г | 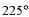 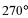 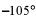 |
Тригонометрические функции в прямоугольном треугольнике
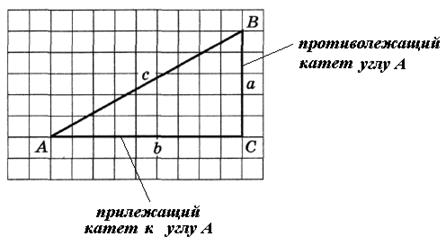
Если а и b — катеты, с — гипотенуза прямоугольного треугольника ABC, то выполняются следующие равенства:
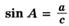
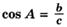
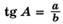
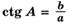
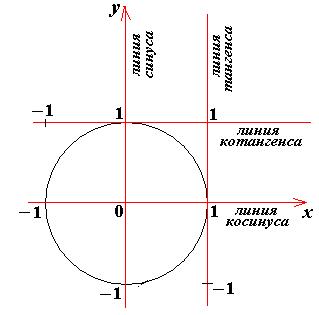
Линии тригонометрического круга
Основные тригонометрические формулы
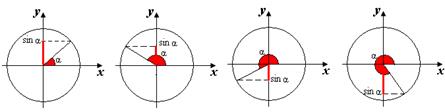
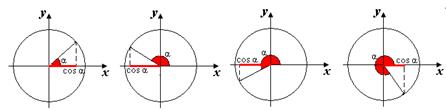
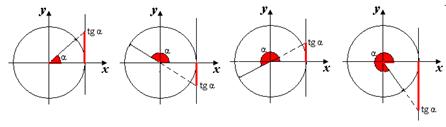
I группа. Соотношения между тригонометрическими функциями одного и того же аргумента:
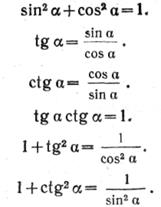
4. Какой знак имеет выражение:
а) 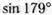 ; б)
; б) 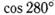 ; в)
; в) 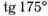 ;
;
г) 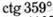 ; д)
; д) 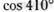 ; е)
; е) 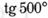 ;
;
ж) 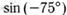 ; з)
; з) 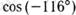 ; и)
; и) 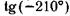
к) 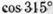 ; л)
; л) 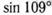 ; н)
; н) 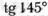 ;
;
о) 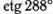 ; п.)
; п.) 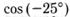 ; р)tg(-10°).
; р)tg(-10°).
| а | + | б | + | в | – |
| г | + | д | + | е | – |
| ж | – | з | – | и | – |
| к | + | л | + | н | – |
| о | + | п | + | р | – |
5. Какой знак имеет выражение:
а) 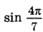 ; б)
; б) 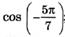 ; в)
; в) 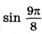 ; г)
; г) 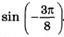
д) 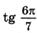 ; е)
; е) 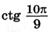 ; ж)
; ж) 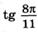 ; з)
; з) 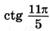
и) 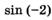 ; к)
; к) 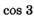 ; л)
; л) 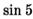 ; м)
; м) 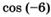
н) 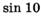 ; о)
; о) 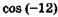 ; п)
; п) 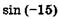 ; р)
; р) 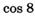 .
.
| а | + | б | – | в | – | г | – |
| д | – | е | + | ж | – | з | + |
| и | – | к | – | л | – | м | + |
| н | – | о | + | п | – | р | – |
6. Определите знак выражения:
а) 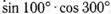 ;
; 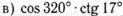 ;
;
б) 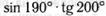 ;
; 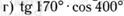
| а | + | в | + |
| б | – | г | – |
7. Определите знак выражения:
а) 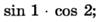 б)
б) 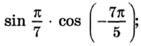
в) 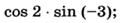 г)
г) 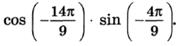
д) 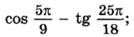 е)
е) 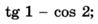
ж) 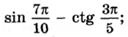 з)
з) 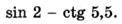
и) 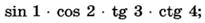
к) 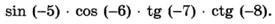
| а | – | б | – |
| в | + | г | – |
| д | – | е | + |
| ж | + | з | + |
| и | + | к | – |
8. По заданному значению функции найдите значения остальных тригонометрических функций:
а) 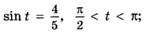 б)
б) 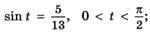
в) 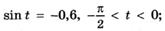 г)
г) 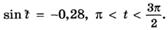
д) 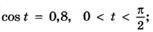 е)
е) 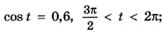
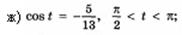 з)
з) 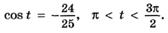
и) 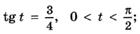 к)
к) 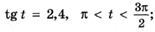
л) 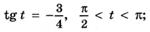 м)
м) 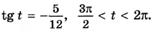
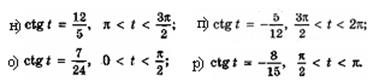
| а | 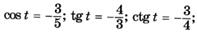 |
| б | 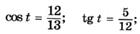 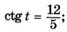 |
| в | 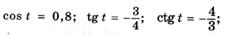 |
| г | 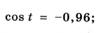 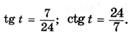 |
| д | 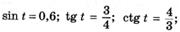 |
| е | 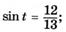 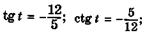 |
| ж | 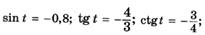 |
| з | 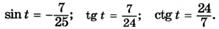 |
| и | 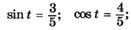 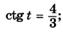 |
| к | 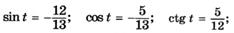 |
| л | 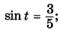 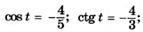 |
| м | 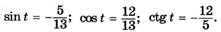 |
| н | 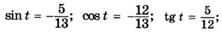 |
| о | 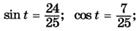 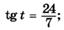 |
| п | 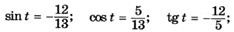 |
| р | 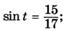 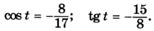 |
II группа. Формулы приведения:
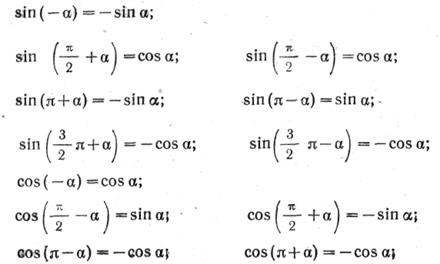
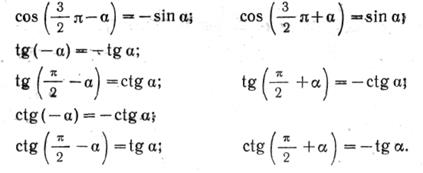
формулы приведения для преобразования выражений вида 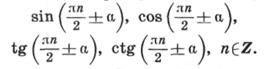
Для запоминания этих формул удобно пользоваться таким мнемоническим правилом:
а) перед приведенной функцией ставится тот знак, который имеет исходная функция, если  ;
;

б) функция меняется на «кофункцию», если пнечетно; функция не меняется, если пчетно.
(Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.)
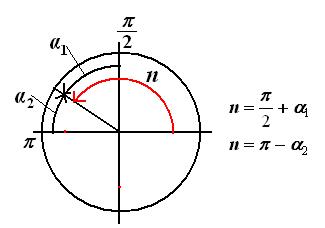
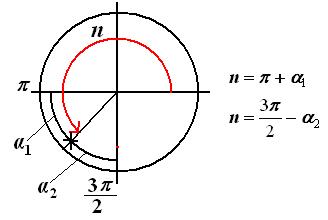
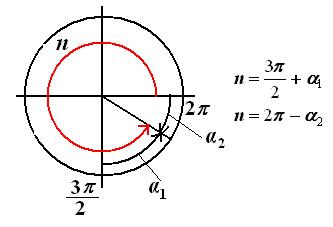
9. Замените тригонометрической функцией угла  :
:
а) 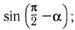 б)
б) 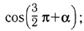 в)
в) 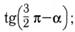
г) 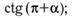 д)
д) 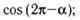 е)
е) 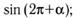
ж) 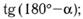 з)
з) 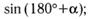 и)
и) 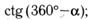
к) 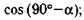 л)
л) 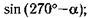 м)
м) 
н) 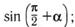 о)
о) 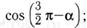 п)
п) 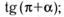
р) 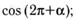 с)
с)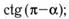 т)
т) 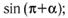
у) 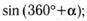 ф)
ф) х)
х) 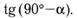
| а | cosα | б | sinα | в | ctgα |
| г | ctgα | д | cosα | е | sinα |
| ж | –tgα | з | – sinα | и | – ctgα |
| к | sinα | л | – cosα | м | – ctgα |
| н | cosα | о | – sinα | п | tgα |
| р | cosα | с | – ctgα | е | – sinα |
| у | sinα | ф | – sinα | х | ctgα |
10. Приведите к тригонометрической функции угла из промежутка 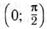 : а)
: а) 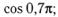 б)
б) 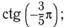
в) 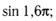 г)
г) 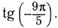
| а | 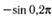 ; ; | б | 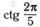 ; ; |
| в | 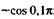 ; ; | г | 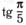 |
11. Приведите к тригонометрической функции угла от 0° до 90°:а) 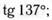 б)
б) 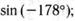
в) 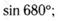 г)
г) 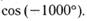
| а | 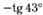 ; ; | б | 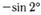 ; ; |
| в | 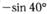 ; ; | г | 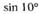 . . |
12. Найдите значение выражения:
а)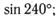 в)
в)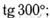 д)
д)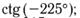
б) 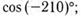 г)
г) 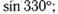 е)
е) 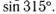
ж)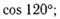 и)
и)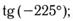 л)
л)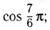
з) 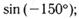 к)
к) 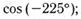 м)
м) 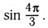
| а | 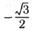 ; ; | в | 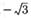 ; ; | д | 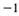 ; ; |
| б | 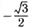 ; ; | г | 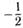 ; ; | е | 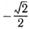 . . |
| ж | а) 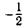 ; ; | и | в) 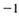 ; ; | л | д) 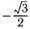 ; ; |
| з | б) 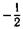 ; ; | к | г) 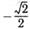 ; ; | м | е) 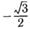 . . |
14. Выразите 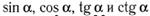 через тригонометрическую функцию угла от 0° до 90°, если:
через тригонометрическую функцию угла от 0° до 90°, если:
а) 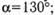 б)
б) 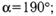
в) 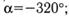 г)
г) 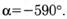
| а | sin130˚=cos40˚ cos130˚=–sin40˚ tg130˚=–ctg40˚ ctg130˚=–tg40˚ | б | sin190˚=–sin10˚ cos190˚=–cos10˚ tg190˚=tg10˚ ctg190˚=ctg10˚ |
| в | sin(–320˚)=sin40˚ cos(–320˚)=cos40˚ tg(–320˚)=tg40˚ ctg(–320˚)=ctg40˚ | г | sin(–590˚)=sin50˚ cos(–590˚)=–cos50˚ tg(–590˚)=–tg50˚ ctg(–590˚)=–ctg50˚ |
15. Найдите 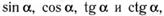 если:
если:
а) 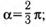 б)
б) 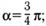 в)
в) 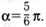
| а | sin 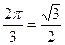 cos cos 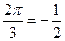 tg tg 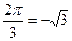 ctg ctg 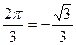 |
| б | sin 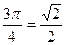 cos cos 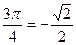 tg tg 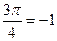 ctg ctg 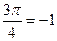 |
| в | sin 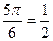 cos cos 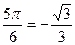 tg tg 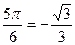 ctg ctg 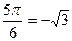 |
16. Преобразуйте выражение:
а) 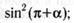 в)
в) 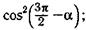
б) 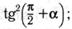 г)
г) 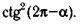
д) 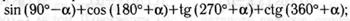
е)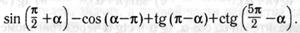
| а | sin2α | в | sin2α | д | |
| б | ctg2α | г | ctg2α | е | 2cosα |
17. Упростите выражение:
а)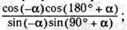 в)
в)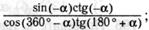
б) 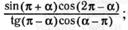 г)
г) 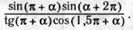
д) 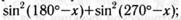
е) 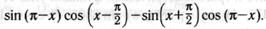
ж)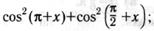 з)
з)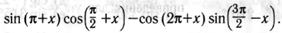
и) 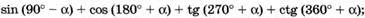
к)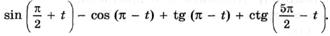
л) 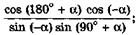 н)
н) 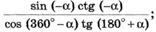
м) 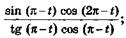 о)
о) 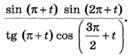
п) 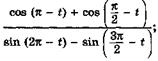
р) 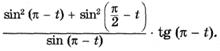
| а | 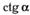 ; ; | д | |
| б | 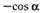 ; ; | е | |
| в | 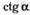 ; ; | ж | |
| г | 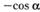 . . | з | |
| и | 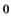 ; ; | н | 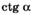 ; ; |
| к | 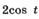 . . | о | 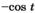 . . |
| л | 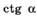 | п | 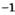 ; ; |
| м | 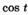 | р | 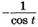 |
18. Вычислите с помощью формул приведения:
а) 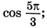 в)
в) 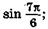
б) 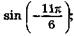 г)
г) 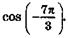
д) 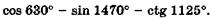 е)
е) 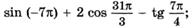
ж) 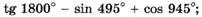
з) 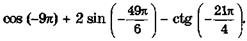
| а | 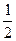 | д | 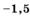 ; ; |
| б | 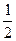 | е | 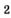 ; ; |
| в | 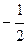 | ж | 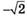 ; ; |
| г | 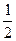 | з | 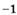 . . |
III группа. Формулы сложения:
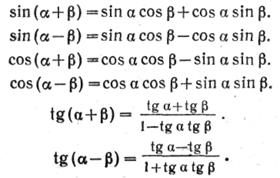
19.С помощью формул сложения преобразуйте выражение:
а) 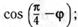 в)
в) 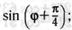
б) 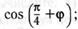 г)
г) 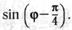
д) 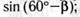 е)
е) 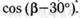
| а | 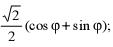 | в | 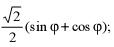 |
| б | 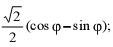 | г | 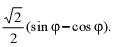 |
| д | 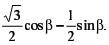 | е | 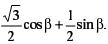 |
20. Представив 105° как сумму 60° + 45°, вычислите:
а) sin 105°; б) cos 105°.
| а | 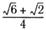 ; ; | б | 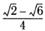 . . |
21.Представив 75° как сумму 30°+45°, вычислите:
а) sin 75°; б) cos 75°.
| а | 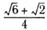 ; ; | б | 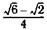 |
22. Упростите выражение:
а) 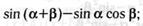 в)
в) 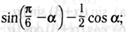
б) 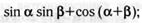 г)
г) 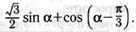
д) 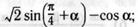 ж)
ж) 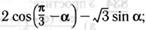
е) 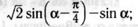 з)
з) 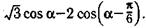
и)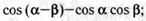 л)
л)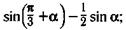
к) 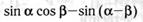 м)
м) 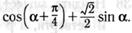
н) 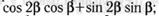 о)
о) 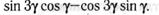
| а | 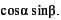 | в | 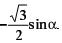 |
| б | 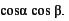 | г | 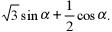 |
| д | 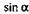 ; ; | ж | 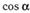 ; ; |
| е | 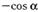 ; ; | з | 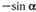 . . |
| и | 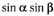 ; ; | л | 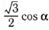 ; ; |
| к | 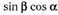 ; ; | м | 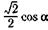 . . |
| н | 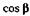 ; ; | о | 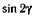 . . |
23. Найдите значение выражения:
а) 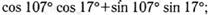
б) 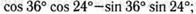
в) 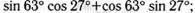 г)
г) 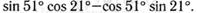
д) 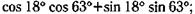
е) 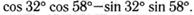
| а | 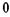 | в | 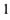 |
| б | 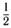 | г | 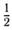 . . |
| д | 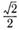 | е | 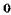 |
24.Упростите выражение:
а) 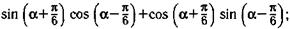
б) 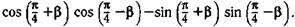
в) 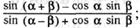 г)
г) 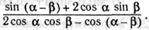
д) 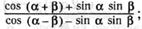 е)
е) 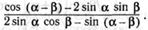
| а | 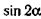 | г | 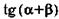 |
| б | 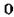 | д | 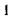 |
| в | 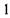 | е | 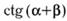 |
25. Зная, что sin 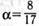 ,
, 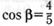 ,
, 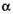 и
и 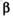 —углы I четверти,
—углы I четверти,
найдите значение выражения:
а) 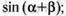 б)
б) 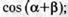 в)
в) 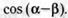
| а | 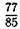 | б | 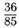 | в | 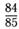 |
26.Известно, что 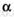 и
и 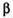 — углы II четверти и
— углы II четверти и 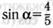 ,
,
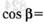
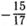 . Найдите:
. Найдите:
а) 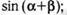 б)
б) 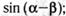
в) 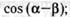 г)
г) 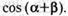
| а | 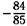 | б | 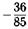 |
| в | 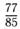 | г | 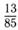 |
27. Вычислите: а) 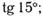 б)
б) 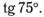
| а | 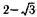 | б | 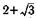 |
28. Известно, что 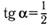 ,
, 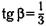 . Найдите:
. Найдите:
а) 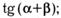 6)
6) 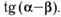
| а | 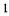 | б | 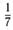 |
