Теорема о необходимом и достаточном условии коллинеарности 2х векторов
Определение.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
Это определение позволяет установить коллинеарность векторов по их изображению на плоскости с некоторой степенью точности, которая зависит от качества чертежа. Поэтому, мы нуждаемся в алгебраическом (а не в геометрическом) условии, выполнение которого будет указывать на коллинеарность двух векторов. Получим его.
Так как операция умножения вектора на число соответствует сжатию или растяжению вектора при неизменном или противоположном направлении, то вектор 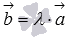 , где
, где 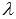 - произвольное действительное число, коллинеарен вектору
- произвольное действительное число, коллинеарен вектору 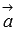 . Справедливо и обратное утверждение: если вектор
. Справедливо и обратное утверждение: если вектор 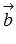 коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 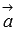 , то он может быть представлен в виде
, то он может быть представлен в виде 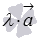 .
.
Таким образом, мы пришли к необходимому и достаточному условию коллинеарности двух ненулевых векторов: для коллинеарности двух векторов 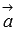 и
и 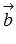 необходимо и достаточно, чтобы они были связаны равенствами
необходимо и достаточно, чтобы они были связаны равенствами 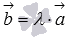 или
или 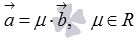 .
.
Перейдем к координатной форме полученного условия коллинеарности двух векторов.
Пусть вектор 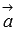 задан в прямоугольной декартовой системе координат на плоскости и имеет координаты
задан в прямоугольной декартовой системе координат на плоскости и имеет координаты 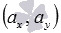 , тогда вектор
, тогда вектор 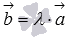 имеет координаты
имеет координаты 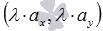 (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор
(при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор 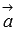 задан в прямоугольной системе координат трехмерного пространства как
задан в прямоугольной системе координат трехмерного пространства как 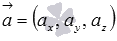 , то вектор
, то вектор 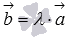 имеет координаты
имеет координаты 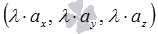 .
.
Следовательно, для коллинеарности двух ненулевых векторов 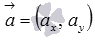 и
и 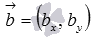 на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:
на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: 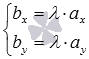 или
или 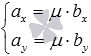 .
.
Для коллинеарности двух ненулевых векторов 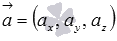 и
и 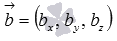 в пространстве необходимо и достаточно, чтобы
в пространстве необходимо и достаточно, чтобы 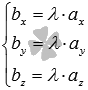 или
или 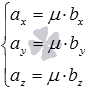 .
.
Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов 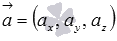 и
и 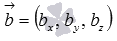 .
.
Если ненулевые векторы 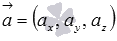 и
и 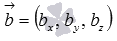 коллинеарны, то по определению векторного произведения
коллинеарны, то по определению векторного произведения 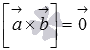 , что равносильно равенству
, что равносильно равенству 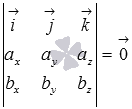 . А последнее равенство возможно лишь тогда, когда векторы
. А последнее равенство возможно лишь тогда, когда векторы 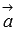 и
и 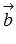 связаны соотношениями
связаны соотношениями 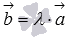 или
или 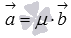 , где
, где 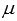 - произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов
- произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов 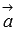 и
и 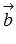 . Таким образом, два ненулевых вектора
. Таким образом, два ненулевых вектора 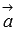 и
и 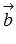 коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
№52
Определение базиса V3
Рассмотрим пространство V3. Любую упорядоченную тройку некомпланарных векторов называют базисом в V3. Выберем в V3 базис, т.е. любые три некомпланарных вектора e1, е2, е3. Эти три вектора с добавленным к ним произвольным четвертым вектором х линейно зависимы. Вектор х является линейной комбинацией векторов
е1, е2, е3:
х = λ1e1 + λ 2е2 + λ 3е3. (1.5)
При этом коэффициенты в представлении определены однозначно, так как векторы е1, е2, е3 линейно независимы.
Параметрические уравнения прямой в пространстве:
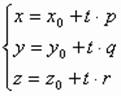
Канонические уравнения прямой в пространстве:
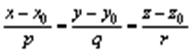
Доказательство.
1. Прямо. Пусть 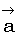 коллинеарен . Докажем, что справедливы равенства
коллинеарен . Докажем, что справедливы равенства 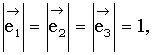 (1).
(1).
Если 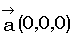 , то доказательство очевидно.
, то доказательство очевидно.
Пусть 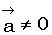 , тогда в силу коллинеарности векторов
, тогда в силу коллинеарности векторов 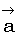 и
и 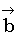 , и по теореме о коллинеарных векторах следует, что
, и по теореме о коллинеарных векторах следует, что 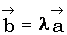 , тогда, согласно теореме 19*(Теорема 19. Каждая координата линейной комбинации векторов, заданная координатой в пространстве, равна той же линейной комбинации соответствующих координат составляющих векторов.
, тогда, согласно теореме 19*(Теорема 19. Каждая координата линейной комбинации векторов, заданная координатой в пространстве, равна той же линейной комбинации соответствующих координат составляющих векторов.
Т. е., если 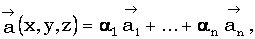 то при условии
то при условии 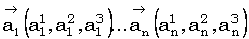 справедливо
справедливо
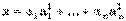
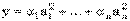
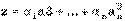 )
)
),* получим 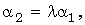
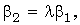
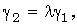
(2)
то есть координаты пропорциональны.
2. Обратно. Пусть выполняется условие (1), докажем, что 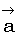 и
и 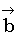 коллинеарны. Так как вектор
коллинеарны. Так как вектор 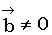 , то условие пропорциональности можно записать в виде
, то условие пропорциональности можно записать в виде 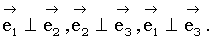 (2). Умножив соотношение (2) соответственно на
(2). Умножив соотношение (2) соответственно на 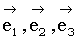 и сложив, получим
и сложив, получим 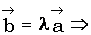
и  коллинеарны.
коллинеарны.
ч.т.д.
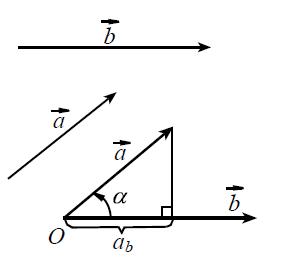
Если из начала и конца вектора опустить перпендикуляры на заданное направление, то отрезок, образованный на данном направлении между концами перпендикуляров, и будет проекцией этого вектора на заданное направление.
Или
1. Проекция вектора на заданное направление. Пусть заданы два
вектора а и b. Приведём эти векторы к одному началу О (рис. 19). Угол, образованный лучами, исходящими из точки О и направленными вдоль векторов а и Ь9 называют углом между векторами а и b. Обозначим этот угол через а.
Число ab=acosa называется проекцией
вектора а на направление вектора b. Проекция вектора а получаете я, если из его конца опустить перпендикуляр на направление вектора b (рис. 19), тогда расстояние от общего начала векторов - точки О - до точки пересечения указанного перпендикуляра с прямой,
на которой лежит вектор b, будет равно модулю проекции вектора а на направление вектора b.
Угол а может принимать различные значения, поэтому в зависимости от знака cos а (см. таблицу выше) проекция может принимать положительные, отрицательные значения или нуль. Проекция равна
нулю, если направления векторов а и b взаимно перпендикулярны. Проекции равных векторов равны. Проекции противоположных векторов отличаются знаком. Легко показать, что проекция суммы векторов равна алгебраической сумме их проекций и что при умножении вектора на число его проекция умножается на то же число.
Общее уравнение плоскости:
Ах + Ву + Сz + D = 0 ,
