Симметрия и асимметрия в композиции, достижение равновесия

Симметрия.В природе большое количество зрительных образов подчиняется закону симметрии. Именно поэтому симметрия легко воспринимается и в композиции. В изобразительном искусстве симметрия достигается таким расположением объектов, что одна часть композиции, как будто являются зеркальным отражением другой. Ось симметрии проходит через геометрический центр. Симметричная композиция служит для передачи покоя, устойчивости, надежности, иногда, величества. Однако создавать изображение абсолютно симметричным не стоит. Ведь в природе не бывает ничего идеального.

Ассиметрия. Ассиметричная композиция – это несимметричная композиция.

Достижение равновесия является одним из самых значимых этапов при построении ассиметричной композиции и часто при этом руководствуются интуитивным чувством равновесия. Чувство это можно развить при помощи различных упражнений.

Равновесие может достигаться противопоставлением размеров, форм пятен цвета и тени.

Если какая-то деталь композиции сильно перевешивает все остальные, то можно попробовать изменить ее цвет, освещенность, форму или уравновесить ее при помощи какого-либо другого предмета, добавленного с противоположной стороны.

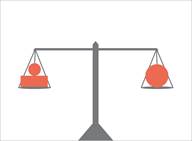
Рис.4. Симметричная и ассиметричная уравновешенные композиции

В математике под симметрией подразумевается совмещение частей фигуры при перемещении ее относительно оси или центра симметрии.

Существуют различные виды симметрии. Простейший вид симметрии зеркальная (осевая), возникающая при вращении фигуры вокруг оси симметрии. Симметрия, возникающая при вращении фигуры вокруг центра вращения называется центральной. Наивысшей степенью симметрии обладает шар, так как в центре его пересекается бесконечное множество осей и плоскостей симметрии. Абсолютная, жесткая симметрия характерна для неживой природы - кристаллов (минералов, снежинок).

Для органической природы, для живых организмов характерна неполная симметрия (квазисимметрия), (например, в строении человека). Нарушение симметрии, асимметрия (отсутствие симметрии) используется в искусстве как художественное средство. Небольшое отклонение от правильной симметрии, то есть некоторая асимметричность, нарушая равновесие, привлекает к себе внимание, вносит элемент движения и создает впечатление живой формы. Различные виды симметрии обладают различным воздействием на эстетическое чувство:

• зеркальная симметрия - равновесие, покой;
• винтовая симметрия вызывает ощущение движения.

В искусстве строгая математическая симметрия используется редко.

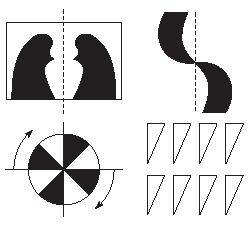
Рис. 5. Виды симметрии: Зеркальная, винтовая, центральная, по сдвигу.

Правильно найденная симметричная композиция воспринимается легко, как бы сразу, независимо от сложности ее построения. Асимметричная же порой требует более длительного осмысления и раскрывается постепенно. Однако утверждение, что симметричная композиция более выразительна, неправомерно. История искусств подтверждает, что асимметрично построенные по законам гармонии композиции ничем не уступают, с точки зрения художественной ценности, симметричным.

Равновесие по-разному проявляется в симметричных и ассиметричных композициях. Симметрия сама по себе не является гарантией уравновешенности композиции. Человек всегда тяготеет к равновесию форм, что создает более полный психологический комфорт, гармонию обитания в предметно-пространственной среде.

МОДУЛЬНЫЕ КОМПОЗИЦИИ

Модуль. Проявлением ритмики и пропорциональных закономерностей является модуль - величина, на основе которой рассчитываются размеры различных форм, сооружений, предметов искусственной среды. В качестве модуля принимают меру длины или размер изделия. Величина произведения или отдельных его частей всегда кратна величине модуля. Модуль придает комплексам, изделиям и их частям соизмеримость, приводит к гармоническому соответствию размеры целого и его частей (золотое сечение). Модуль активно внедряется в сферу предметной деятельности человека. Модульные размеры деталей различных конструкций обеспечивают их унификацию и массовость производства.

Модульная структура.Композиция модульной структуры объединяет частные моменты построения художественной формы (реальное или иллюзорное формирование пространства и объема, симметрия и асимметрия, масштаб, ритм и пропорции, нюанс и контраст, перспектива, группировка, соотношение целого и деталей, цветовое решение и т.д.). В модульной структуре композиция организует как внутреннее построение произведения, так и его соотношение с окружающей средой, координирует его восприятие зрителем.

При разработке модульной структуры следует учитывать, что ее композиционную основу составляет идейное содержание, а формальные приемы композиции (симметрия, асимметрия, контрасты, ритм и т.п.) лишь служат средством выражения этого содержания.

Золотое сечение

Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е.

а:в=в: (а -в)

• Отношение з. с. выражается числом 0,618.
• Пропорция з. с. 1:0,618=0,618:0,382.

Если отрезок прямой выразить через единицу, а затем разделить его на два отрезка по з. с., то больший отрезок будет равен 0,618, а меньший 0,382.

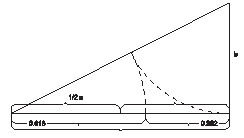
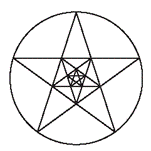
рис 5. Деление отрезка по золотому сечению

На основании пропорции золотого сечения был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к 0,618, то есть, к отношению золотого сечения.

Пропорции золотого сечения ученые связывают с развитием органической материи. Золотое сечение было обнаружено в объектах живой природы - в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его наблюдали в устройстве вселен ной в расположении планет. В отношении золотого сечения находятся так же элементы геометрических фигур - пятиугольника, звезды .

В прямоугольнике стороны находятся в отношении золотого сечения. Этот прямоугольник содержит в себе квадрат и малый прямоугольник золотого сечения (его большая сторона является малой стороной первоначального прямоугольника.) Поэтому можно построить прямоугольник золотого сечения на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится прямоугольник.

Точки пересечения линий, составляющих звезду, делят их на отрезки в отношении золотого сечения. Этот малый прямоугольник подобен большому прямоугольник, составленному из квадрата и малого прямоугольника золотого сечения, то есть оба эти прямоугольника являются прямоугольниками золотого сечения.

Иначе говоря, если отсечь от прямоугольника золотого сечения квадрат, то остается меньший прямоугольник, стороны которого опять же будут находиться в отношении золотого сечения. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник золотого сечения и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют "кривая развития", "спираль жизни", ибо в ней как бы заложена идея бесконечного развития.

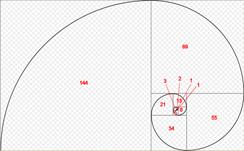
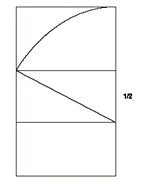
Рис.6. Построение прямоугольника золотого сечения на основе квадрата.

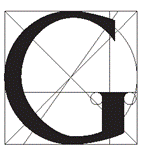
Рис. 7. Построение буквы из книги Луки Пачоли "О божественной пропорции"\

Греческие ремесленники, создавая гончарные изделия также применяли золотое сечение. В эпоху Возрождения золотое сечение использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли его в поисках гармоничных пропорций букв. Прямоугольник золотого сечения встречаетсяи в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции золотого сечения позволяют красиво организовать пространство книжной страницы и разворота.

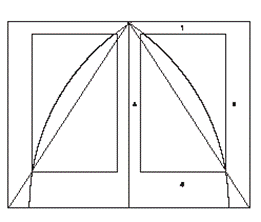
Рис. 8. Схема идеальных пропорций средневековой рукописи.

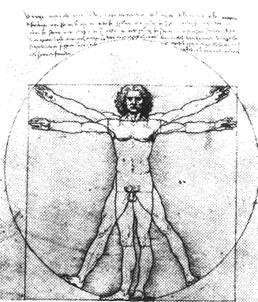Рис. 9. Леонардо да Винчи. Божественный канон.

На рисунке Леонардо да Винчи изображена связь квадрата и круга с человеческой фигурой известная еще древним. Квадрат является устойчивой, статичной фигурой. Она ассоциируется с чем_то неподвижным, завершенным. В Древнем мире у некоторых народов изображение квадрата было связано с символикой смерти. В этой связи интересно заметить, что пропорции квадрата в природе встречаются в формах неживой материи, у кристаллов. Благодаря своей статической завершенности квадрат используется в прикладной графике, в области визуальных коммуникаций наряду с формой круга как элемент, фиксирующий внимание, а также для ограничения пространства, на котором сосредоточена информация.

Пропорционирование - приведение частей целого к единому пропорциональному строю.Пропорции есть соответствие между элементами произведения и его целым по отношению к части, принятой за исходную, на чем основана всякая соразмерность. Ибо дело в том, что никакой храм без соразмерности и пропорций не может иметь правильной композиции, если в нем не будет точно такого же членения, как у хорошо сложенного человека.

В ХХ веке вновь возродился интерес к золотому сечению как к способу пропорционирования. Оно привлекло внимание архитекторов. Советский архитектор Жолтовский и француз Корбюзье занимались проблемами золотого сечения и использовали его в своей архитектурной практике, Корбюзье создал целую систему пропорционирования на основе чисел ряда золотого сечения и пропорций человеческого тела и назвал ее "Модулор", что по-латыни означает "ритмически размерять".

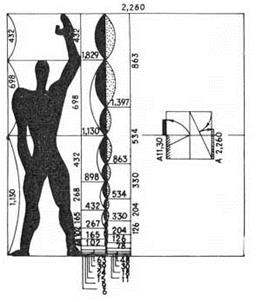
Рис. 10. Модулор Корбюзье

Модулор Корбюзье представляет собой гармонические ряды чисел, которые связаны в единую систему и предназначены для использования в архитектуре и дизайне –для гармонизации всей среды, в которой обитает человек. Корбюзье мечтал о перестройке с помощью Модулора всей архитектурной и предметной среды. Сам он создал несколько прекрасных образцов архитектуры, но о более широком применении Модулора в существующих условиях не могло быть и речи.

Модулор использовался в ряде слуйаев в дизайне и в графическом дизайне - при конструировании печатных изданий. На рис. 10 приводятся варианты деления прямоугольника 3:4, приведенные Корбюзье для демонстрации возможностей конструирования с помощью Модулора.

В основе преподавания композиции при подготовке дизайнеров и специалистов по рекламе лежит беспредметная композиция. Иначе такую композицию называют формальной или абстрактной. В основе преподавания данного вида композиции положены достижения художников русского авангарда.

Прежде всего необходимо знать, что такое композиция на модульной основе.

Композиция на модульной основе – это композиция, построенная на основе повторяющихся элементов – модулей (элементов или группы элементов), которые связанны определенным ритмом построения.

Одной из разновидностей модульной композиции является супрематическая композиция.

Супрематическая композиция – это композиция, элементами которй являются геометрические примитивы (круг, квадрат, прямоугольник, треугольник, линия)

На данных занятиях студенты выполняют уравновешенные супрематические композиции (симметричны и ассиметричные).

Правильно найденная симметричная композиция воспринимается легко, независимо от сложности ее построения. Ассиметричная порой требует более длительного осмысления и раскрывается постепенно.

Симметрия применяется не только в плоскостных композициях, но и в объемно-пространственных.

Первый разговор о гармонии в композиции, и ее основном непременном условии – равновесии, приводит к логическому выводу о том, что все взаимозависимо; и количество элементов, и их конфигурация, и их соотношение с композиционной плоскостью и между собой.

Любая композиция может быть статической и динамической. Проще всего рассмотреть понятия статики и динамики на примере супрематических композиций.

Статическая композиция – это композиция, все элементы которой расположены горизонтально или под углом 90. Такие композиции ассоциируются с состоянием покоя и стабильности.

Динамическая композиция – это композиция, все элементы которой расположены под углами 30 и 45 градусов. Такие композиции ассоциируются с движением и развитием.

Рис. 11. Супрематические композиции (статика и динамика).