Общее представление о симметрии
Одно из наиболее популярных определений понятия симметрии принадлежит немецкому математику Герману Вейлю:
«Если я не ошибаюсь, в нашем повседневном языке слово «симметрия» употребляется в двух значениях. В первом смысле, «симметричное» означает нечто, обладающее хорошим соотношением пропорций, уравновешенное. А во втором смысле «симметрия» обозначает тот вид согласованности отдельных частей, который объединяет их в единое целое»
«симметрия – есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство».
В словаре С.И. Ожегова мы встречаем такое определение: симметрия - соразмерность, пропорциональность в расположении частей чего-нибудь по обе стороны от середины, центра.
«На земле жизнь зародилась в сферически симметричных формах…: образовался мир растений, обладающих симметрией конуса, и мир животных с зеркальной симметрией».
М.Гарднер
О симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в Ёлочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой творение мороза!
В жизни нас окружают удивительные по красоте и разнообразию творения природы и человека. Мы настолько привыкли видеть их вокруг себя, что не замечаем, каким удивительными свойствами они обладают. Задумывались ли вы когда-нибудь над такими вопросами:
- почему нам нравится рассматривать цветок, снежинку или кристалл (Они привлекают нас своей красотой и пропорциональностью);
- почему нас привлекают создания художников, скульпторов, зодчих (Правильность формы того или иного объекта определяется не только законами красоты, но и её целесообразностью, полезностью);
-почему нас так зачаровывает ритм музыки и стихов, что подчас они ещё долго звучат в голове помимо нашего желания (Музыка содержит повтор с небольшим отклонением от строгой симметрии, что делает её более выразительной);
- почему каждый день сменяет ночь, а ей на смену приходит следующий день (по законам природы);
- почему неизменно каждый год за зимой приходит весна, а ей на смену – лето, потом – осень, зима, и цикл начинается с самого начала (каждый год зима сменяет осень и растения как бы умирают, сбрасывая листья, но каждую весну возвращаются к жизни, вновь покрываясь листвой);
Эти вопросы позволяют вам обратить внимание на многие интересные закономерности в окружающем нас мире.
Идея симметрии возникла у древнегреческих философов и математиков в связи с учением о гармонии мира. Они считали симметрию одной из самых важных основ гармонии. Греческому слову «гармония» не менее трёх тысяч лет, и означает оно согласованность, стройность в сочетании чего-либо. Именно по законам гармонии, используя свойство симметрии, создавали свои шедевры ещё древние ваятели, живописцы, зодчие. Многие их творения мы можем видеть и в наши дни. Вспомните величественные пирамиды, построенные 5 тысяч лет назад на берегу реки Нила в Египте, или великолепные храмы, возведённые в Древней Греции. И в современном понимании гармония – это соразмерность частей и органичное слияние различных компонентов в единое целое.
Существует старинная притча о буридановом осле. У одного философа по имени Буридан был осел. Однажды, уезжая надолго, философ положил перед ним две совершенно одинаковые охапки сена: одну слева, а другую – на таком же расстоянии – справа. Бедное животное не смогло решить, с какой охапки начать есть, и… умерло с голоду.
В данной притче с математической точки зрения правый и левый объекты настолько одинаковы, что их можно считать равноправными, за что и поплатился бедный осел.
Тело животного, например кошки, состоит из двух половин: левой и правой, оно может быть получено повторением оной из них – то есть обладает симметрией. Такой же симметрией обладает тело человека.
Большинство растений тоже симметричны. Однако у многих из них какая- либо часть может повторяться два раза и более. Например, каждому хочется, чтобы его новогодняя ёлка была красивой, чтобы её ветки повторялись равномерно вдоль ствола, так и вдоль него.
Симметрия хорошо видна у бабочек. Можно сказать, что каждое животное, насекомое, рыба, птица состоит из правой и левой половин .
Придуманный в известной сказке о докторе Айболите фантастический Тянитолкай представляется совершенно невероятным существом, у него симметричны передняя и задняя половины.
Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. С симметрией мы часто встречаемся в искусстве. архитектуре. технике. быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях.
От композиции здания в первую очередь зависит впечатление, которое производит архитектурное сооружение. Сочетание различных объемов - высоких и низких, прямолинейных и криволинейных, чередование пространств - открытых и закрытых - вот основные приемы, которые использует зодчий, создавая архитектурные композиции.
Гармония Наиболее ясны и уравновешены здания с симметричной композицией. Такие здания были характерны для архитектуры эпохи классицизма.
Впечатление от здания во многом зависит от ритма, т.е. от четкого распределения и повторения в определенном порядке объемов зданий или отдельных архитектурных форм на здании (колонн, окон, рельефов и т.д.). Преобладание элементов вертикального ритма - колонн, арок, проемов, пилястр - создает впечатление облегченности, устремленности вверх. Наоборот, горизонтальный ритм - карнизы, фризы, пояса и тяги - придает зданию впечатление приземистости, устойчивости.
«Душа музыки – ритм – состоит в правильном периодическом повторении частей музыкального произведения, - писал в 1908 году известный русский физик Г.В. Вульф. – Правильное же повторение одинаковых частей в целом и составляет сущность симметрии. Мы с тем большим правом можем приложить к музыкальному произведению понятие симметрии, что это произведение записывается при помощи нот, т.е. получает пространственный геометрический образ, части которого мы можем обозревать». Он же писал: «Подобно музыкальным произведениям, могут быть симметричны и произведения словесные, в особенности стихотворения». В стихотворениях подразумевается симметрия чередования рифм, ударных слогов, то есть опять таки ритмичность. Композитор в своей симфонии может по нескольку раз возвращаться к одной и той же теме, постепенно разрабатывая ее. Сохранение темы и ее изменение (разработка, развитие) – это и есть единство симметрии и асимметрии. И чем удачнее решает композитор или поэт проблему соотношения между симметрией и асимметрией, тем выше художественная ценность создаваемого произведения искусства. Самое непосредственное отношение к симметрии имеет композиция. Великий немецкий поэт Иоганн Вольфганг Гете утверждал, что «всякая композиция основана на скрытой симметрии». Владеть законами композиции – это значит владеть законами симметрии. Три основных закона композиции предполагают трансляционно-тождественное повторение элементов структуры, контрастное повторение, варьированное повторение. Это выглядит как орнамент во времени.
Симметрия воспринимается человеком как проявление закономерности, порядка в природе, а это в значительной мере определяет его жизнь и деятельность.
Подражая природе, люди создают мир искусства и техники, основываясь на симметрии как основном принципе гармонии.
Виды симметрии
Центральная симметрия
Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О.
Если фигура при повороте плоскости вокруг некоторой точки самосов мещается за полный оборот не менее двух раз, то говорят, что она обладает симметрией относительно этой точки.
Количество самосовмещений фигуры за полный оборот называет порядком симметрии относительно точки.
Две точки А и А1 называются симметричными относительно точки О, если О - середина отрезка АА1. Точка О считается симметричной самой себе.

Симметрия относительно точки
На рисунке точки М и М1, N и N1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
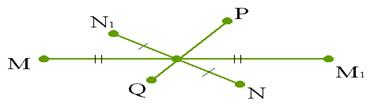
Фигура называется симметричной относительно точки О
если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
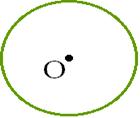
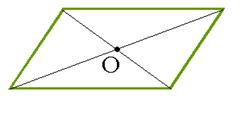
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей.
Осевая симметрия
Осевая симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Каждая точка прямой а считается симметричной самой себе.
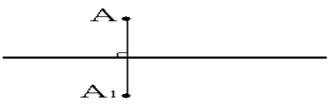
Симметрия относительно прямой
если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией. 
У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла
Равнобедренный(но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник - три основные симметрии.
Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а квадрат - четыре оси симметрии.
У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.
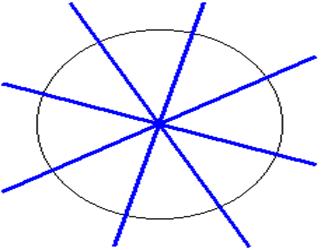
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
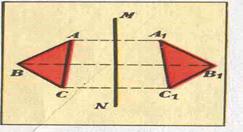
Зеркальная симметрия
Что может быть больше похоже на мою руку или мое ухо , чем их собственное отражение в зеркале ? И все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки.
Иммануил Кант
Если каждая из половинок объекта является зеркальным отражением другой, относительно разделяющей их воображаемой плоскости, то говорят, что объект обладает зеркальной симметрии.
Зеркальная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.
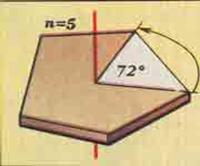
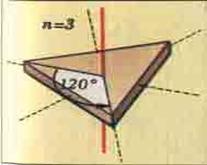
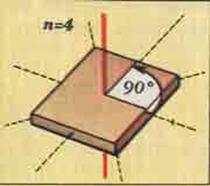
Поворотная симметрия
Поворотная симметрия - это такая симметрия при которой объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n, где n = градусной мерой угла.
Если объект при вращении вокруг некоторой прямой самосовмещается за полный оборот не менее двух раз, то говорят, что он обладает поворотной симметрией. Прямую, вокруг которой объект вращается, называют поворотной осью, а количество самосовмещений объекта за полный оборот – порядком поворотной оси.