Правила равенства, суммы и произведения
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Составители: В.Е.Алексеев, В.В.Лозин
Комбинаторика (комбинаторный анализ) – раздел дискретной математики, в котором изучаются объекты, составленные из элементов конечных множеств. Одним из основных видов комбинаторных задач являются перечислительные задачи. В этих задачах речь идет о выборе определенного количества элементов из некоторого множества с соблюдением тех или иных условий и требуется подсчитать число способов, которыми можно осуществить такой выбор.
Напомним некоторые обозначения из теории множеств.
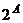 – множество всех подмножеств множества A.
– множество всех подмножеств множества A.
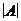 – число элементов (мощность) конечного множества A.
– число элементов (мощность) конечного множества A.
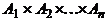 – прямое (декартово) произведение множеств
– прямое (декартово) произведение множеств 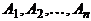 . Элементами декартова произведения являются последовательности вида
. Элементами декартова произведения являются последовательности вида 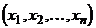 , где
, где 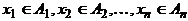 . При
. При 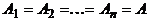 получается декартова степень
получается декартова степень 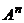 множества A. Если элементы множества A считать буквами алфавита, то элементы декартовой степени можно рассматривать как слова, они в этом случае записываются в виде
множества A. Если элементы множества A считать буквами алфавита, то элементы декартовой степени можно рассматривать как слова, они в этом случае записываются в виде 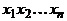 .
.
Буквой E будем обозначать двухэлементное множество 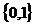 .
.
Символом отмечается конец доказательства.
Задачи
1. Имеется 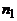 разных книг одного автора,
разных книг одного автора, 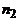 – второго и
– второго и 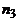 – третьего. Каким числом способов можно выбрать
– третьего. Каким числом способов можно выбрать
а) одну книгу?
б) две книги разных авторов?
в) три книги разных авторов?
2.Какимчислом способов можно заполнить анкету, содержащую n вопросов, если на каждый вопрос можно ответить
а) “да” или “нет”?
б) “да”, “нет”, “не знаю”?
3. Сколько слов длины n можно составить, если в алфавите q букв? Сколько среди них палиндромов (слов, читающихся одинаково слева направо и справа налево)?
4. Сколько матриц с m строками и n столбцами можно составить из элементов 0 и 1 ?
5.Сколько слов длины n в q–буквенном алфавите, в которых любые две соседние буквы различны?
6.Каким числом способов можно на обычной шахматной доске разместить белую и черную ладьи так, чтобы они не атаковали друг друга?
7. Сколько бинарных отношений можно определить на множестве из n элементов? Сколько среди них
а) рефлексивных?
б) симметричных?
в) антисимметричных?
Перестановки и сочетания
В простейших комбинаторных задачах требуется подсчитать число способов выбрать k элементов из n–элементного множества. То, что получается в результате выбора, называется выборкой из n по k или (n,k)–выборкой.
Понятие выборки отличается от понятия подмножества. Первое отличие состоит в том, что в выборках может допускаться повторение элементов. Это означает, что в выборку может входить несколько экземпляров одного и того же элемента. В этом случае говорят, что рассматриваются выборки с повторениями. Другое отличие – выборки могут быть упорядоченными или неупорядоченными. Упорядоченность означает, что выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, считаются различными. Если же такие выборки считаются одинаковыми, то говорят, что рассматриваются неупорядоченные выборки. Упорядоченные выборки называют перестановками (или размещениями), неупорядоченные – сочетаниями. Таким образом, имеется четыре основных типа выборок: перестановки (без повторений), перестановки с повторениями, сочетания (без повторений) и сочетания с повторениями.
Подсчитаем число выборок каждого типа. Множеством, из которого делается выбор, будем считать множество чисел 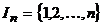 .
.
Перестановки с повторениями. Перестановки с повторениями из n по k – это последовательности длины k, состоящие из элементов множества 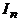 , то есть попросту элементы множества
, то есть попросту элементы множества 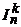 . Из теоремы 1 поэтому следует
. Из теоремы 1 поэтому следует
Теорема 3. Число (n,k)– перестановок с повторениями равно 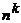 .
.
Перестановки. Обозначим число перестановок из n по k через 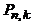 .
.
Теорема 4. 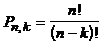 .
.
Д о к а з а т е л ь с т в о. В качестве первого элемента перестановки может быть выбран любой из n элементов множества 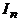 . Поскольку повторения недопустимы, второй элемент можно выбрать
. Поскольку повторения недопустимы, второй элемент можно выбрать 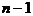 способами, третий
способами, третий 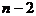 способами и т.д. Применяя обобщенное правило произведения, получаем
способами и т.д. Применяя обобщенное правило произведения, получаем
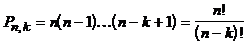 .
.
В частности, при 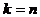 получается формула для числа перестановок всех n элементов:
получается формула для числа перестановок всех n элементов:
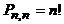
Сочетания. Сочетания из n по k, то есть неупорядоченные выборки без повторений, это просто k–элементные подмножества n–элементного множества. Число (n,k)–сочетаний обозначается через 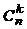 или
или 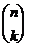 .
.
Теорема 5. 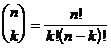 .
.
Д о к а з а т е л ь с т в о. Выписывая элементы (n,k)–сочетания в некотором порядке, получаем (n,k)–перестановку. Поскольку k элементов можно упорядочить 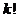 способами , то из каждого сочетания можно образовать
способами , то из каждого сочетания можно образовать 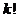 различных перестановок. Из всех
различных перестановок. Из всех 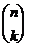 сочетаний таким образом получится
сочетаний таким образом получится 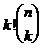 перестановок. Ясно, что каждая перестановка будет при этом получена точно один раз. Следовательно,
перестановок. Ясно, что каждая перестановка будет при этом получена точно один раз. Следовательно, 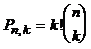 . Применяя формулу для числа перестановок, получаем утверждение теоремы.
. Применяя формулу для числа перестановок, получаем утверждение теоремы.
В качестве простейшего примера применения формулы для числа сочетаний рассмотрим следующую задачу.
Задача 1. Определить число слов длины n в алфавите E, содержащих в точности k единиц.
Р е ш е н и е . Так как сочетания являются подмножествами, то их можно задавать с помощью характеристических векторов, как описано в доказательстве теоремы 2. Характеристический вектор, соответствующий (n,k)–сочетанию, имеет n компонент, среди которых ровно k единиц. Этот вектор можно рассматривать также как слово в алфавите E. Таким образом, имеется взаимно однозначное соответствие между (n,k)–сочетаниями и словами длины n в алфавите E. Отсюда следует, что число таких слов равно 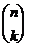 .
.
Сочетания с повторениями.
Теорема 6. Число (n,k)–сочетаний с повторениями равно 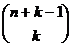 .
.
Д о к а з а т е л ь с т в о . Для того, чтобы задать сочетание с повторениями из n по k, достаточно указать для каждого числа от 1 до n, сколько раз оно встречается в данном сочетании. Пусть 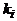 – количество вхождений числа i в сочетание, i = 1,2,...,n. Так как общее число элементов в сочетании равно k, то
– количество вхождений числа i в сочетание, i = 1,2,...,n. Так как общее число элементов в сочетании равно k, то 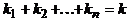 . Поставим в соответствие данному сочетанию слово в алфавите E следующим образом. В начале слова поставим
. Поставим в соответствие данному сочетанию слово в алфавите E следующим образом. В начале слова поставим 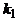 нулей, после них единицу, за ней
нулей, после них единицу, за ней 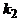 нулей, после них вторую единицу, и т.д. Все слово будет состоять из n групп нулей, разделенных единицами, причем в i–той группе (считая слева) число нулей равно
нулей, после них вторую единицу, и т.д. Все слово будет состоять из n групп нулей, разделенных единицами, причем в i–той группе (считая слева) число нулей равно 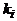 . Заметим, что после последней группы единица не ставится, т.е. слово оканчивается
. Заметим, что после последней группы единица не ставится, т.е. слово оканчивается 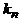 нулями. Всего, таким образом, будет k нулей и
нулями. Всего, таким образом, будет k нулей и 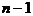 единица, а длина слова равна
единица, а длина слова равна 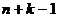 . Обратно, если взять любое слово, то по нему можно построить (n,k)–сочетание с повторениями: нули разбиваются единицами на n групп и число i необходимо включить в сочетание столько раз, сколько нулей в i–той группе. Таким образом, имеется взаимно однозначное соответствие между (n,k)–сочетаниями с повторениями и словами длины
. Обратно, если взять любое слово, то по нему можно построить (n,k)–сочетание с повторениями: нули разбиваются единицами на n групп и число i необходимо включить в сочетание столько раз, сколько нулей в i–той группе. Таким образом, имеется взаимно однозначное соответствие между (n,k)–сочетаниями с повторениями и словами длины 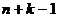 в алфавите E, содержащими ровно k нулей. Число таких слов, как было показано выше, равно
в алфавите E, содержащими ровно k нулей. Число таких слов, как было показано выше, равно 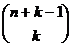 . ?
. ?
Задачи
1. Сколько имеется вариантов выбора трех призеров среди n участников конкурса
а) с указанием занимаемых ими мест?
б) без указания мест?
2.Сколько отношений линейного порядка можно определить на множестве из n элементов?
3. Сколькими способами можно расставить 8ладей на обычной шахматной доске размером так, чтобы они не угрожали друг другу, т.е. чтобы никакие две из них не стояли на одной вертикали или горизонтали?
4. Сколько имеется перестановок из элементов1,2,...,n, в которых
а) 1 стоит раньше 2?
б) 1 и 2 не стоят рядом?
в) между 1 и 2 расположены k других элементов?
5.На плоскости расположены n точек, никакие три из которых не лежат на одной прямой. Сколько существует треугольников с вершинами в данных точках?
6. Каким числом способов можно разделить 10 юношей на две баскетбольные команды по 5 человек в каждой?
7.Каким числом способов можно расположить n нулей и k единиц в последовательность так, чтобы никакие две единицы не стояли рядом?
8.Каким числом способов можно составить букет из n цветов трех видов, если все цветы одного вида одинаковы и имеется неограниченный запас цветов каждого вида?
9.Определите число целых а) положительных; б) неотрицательных решений уравнения 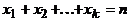 .
.
. . . . . . . . . . . . . .
В этой бесконечной таблице строка с номером n (n = 0,1,2,...) образована числами 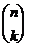 , k пробегает все значения от 0 до n. При этом каждая следующая строчка сдвинута относительно предыдущей таким образом, что непосредственно над числом
, k пробегает все значения от 0 до n. При этом каждая следующая строчка сдвинута относительно предыдущей таким образом, что непосредственно над числом 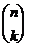 левее и правее его оказываются расположены числа
левее и правее его оказываются расположены числа 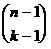 и
и 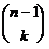 , сумма которых, по свойству 4°, как раз и равна
, сумма которых, по свойству 4°, как раз и равна 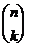 . Таким образом, если строка с номером
. Таким образом, если строка с номером 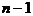 заполнена, то легко заполняется строка с номером n: первый и последний элементы всегда равны 1, а каждый из остальных получается сложением двух расположенных над ним элементов предыдущей строки.
заполнена, то легко заполняется строка с номером n: первый и последний элементы всегда равны 1, а каждый из остальных получается сложением двух расположенных над ним элементов предыдущей строки.
Некоторые свойства биномиальных коэффициентов легко выводятся из бинома Ньютона. Приведем два из них.
5°. 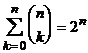 . Это получается из формулы бинома, если положить
. Это получается из формулы бинома, если положить 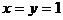 .
.
6°. 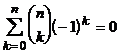 . Это получается при
. Это получается при 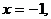
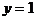 .
.
Задачи
1. Докажите тождества:
1) 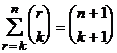 (совет: воспользуйтесь свойством 4°);
(совет: воспользуйтесь свойством 4°);
2) 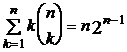 ;
;
3) 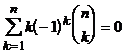 .
.
2. Докажите, что число слов длины n в алфавите E, имеющих четное число единиц, равно 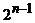 .
.
Задачи
1. Сколько различных слов можно составить, переставляя буквы в слове “математика”?
2. Каким числом способов можно разбить 14 человек на 7 пар?
3. Каким числом способов можно разместить 7 студентов в трех комнатах общежития - одно-, двух- и четырехместной?
4. Код замка состоит из пяти десятичных цифр. Известно, что среди них один раз встречается цифра 0 и дважды - цифра 3. Сколько комбинаций нужно перебрать, чтобы наверняка открыть замок?
5. Чему равен коэффициент при 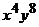 в разложении
в разложении 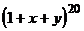 ?
?
Задачи
1.На одной из кафедр университета работают тринадцать человек, причем каждый из них знает хотя бы один иностранный язык. Десять человек знают английский, семеро - немецкий, шестеро - французский. Пятеро знают английский и немецкий, четверо - английский и французский, трое - немецкий и французский.
Сколько человек знают все три языка?
Сколько человек знают ровно два языка?
Сколько человек знают только английский язык?
2. В музыкальном ансамбле используется четыре инструмента, Для каждого инструмента в ансамбле имеется четыре человека, владеющих данным инструментом, для любых двух инструментов - три человека, играющих на них, для любых трех - два человека. Один человек владеет всеми четырьмя инструментами. Сколько человек в ансамбле?
6. Задачи для самостоятельной работы
1. Имеется 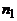 разных книг одного автора,
разных книг одного автора, 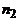 – второго и
– второго и 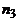 – третьего. Каким числом способов можно выбрать
– третьего. Каким числом способов можно выбрать
а) две книги одного автора?
б) три книги одного автора?
в) одну книгу первого автора, две – второго и три – третьего?
2.Каким числом способов можно на шахматной доске поместить черного и белого королей так, чтобы они не атаковали друг друга?
3. На одной из двух параллельных прямых зафиксировано n точек, а на другой - m точек. Сколько имеется
а) треугольников;
б) четырехугольников
с вершинами в данных точках?
4. Каким числом способов из 10 человек можно выбрать три комиссии, если в первой и во второй должно быть по 3 человека, а в третьей - 5 человек, и ни один из членов первой комиссии не должен входить во вторую и третью?
5. Траекторией назовем ломаную линию на плоскости, состоящую из отрезков, параллельных координатным осям, причем длины отрезков - целые числа, а при движении вдоль ломаной от начальной точки каждый вертикальный отрезок проходится снизу вверх, а горизонтальный - слева направо. Найдите число траекторий, начинающихся в точке (0,0), а оканчивающихся
а) в точке (m,n);
б) на прямой 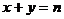 .
.
6. Сколько диагоналей у выпуклого n-угольника? Найдите число точек пересечения этих диагоналей (не считая вершин), если известно, что в каждой из этих точек пересекаются только две диагонали?
7. Имеется колода из 4n карт четырех мастей, по n карт каждой масти, занумерованных числами 1,2,...,n. Каким числом способов можно выбрать пять карт так, чтобы среди них оказались :
а) пять карт одной масти с последовательными номерами;
б) четыре карты с одинаковыми номерами;
в) три карты с одним номером и две с другим;
г) пять карт одной масти;
д) пять карт с последовательными номерами;
е) три карты с одинаковыми номерами;
ж) две карты с одинаковыми, остальные с разными номерами.
8. Сколько имеется шестизначных десятичных чисел, у которых
а) есть одинаковые цифры?
б) цифры идут в возрастающем порядке?
в) ровно три цифры четные?
г) не менее двух четных цифр?
д) все цифры различны, причем первая - не 9, а последняя - не 0?
е) сумма цифр четна ?
9. Сколько существует отображений множества A в множество B, если ÷A÷=n, ÷B÷=m? Сколько среди них инъективных? Биективных?
10 Дано множество U из n элементов и в нем подмножество A из k элементов. Определите число подмножеств 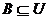 , удовлетворяющих условию
, удовлетворяющих условию
а) 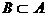 ; г)
; г) 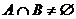 ; ж)
; ж) 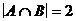 ;
;
б) 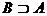 ; д)
; д) 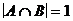 ; з)
; з) 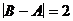 ;
;
в) 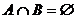 ; е)
; е) 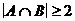 ; и)
; и) 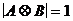 .
.
11. В множестве U из n элементов, найдите число пар подмножеств (A,B) удовлетворяющих условиям:
а) 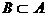 ; г)
; г) 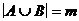 ,
, 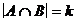 ;
;
б) 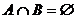 ; д)
; д) 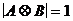 ;
;
в) 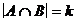 ; е)
; е) 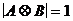 ,
, 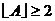 ,
, 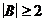 .
.
12. Определите число матриц с m строками и n столбцами, составленных из элементов 0 и 1, у которых строки попарно различны.
13. Каким числом способов можно разложить p черных и q белых шаров по k различным ящикам?
14. Каким числом способов можно разместить n различных предметов по k различным ящикам? Сколько таких размещений, при которых в каждый ящик укладывается не более одного предмета?
15. Каким числом способов можно распределить n одинаковых монет между k лицами? Сколько таких способов, при которых каждый получает не менее одной монеты?
16. Каким числом способов можно kn различных предметов разложить по n одинаковым (неразличимым) ящикам так, чтобы в каждом ящике оказалось ровно k предметов?
17 Каким числом способов 7 человек могут разместиться в трех автомобилях, если в первом из них имеется 2 свободных места, во втором - 3, а в третьем - 4?
18. В следующих заданиях рассматриваются слова в алфавите 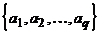 . Через
. Через 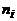 обозначается число вхождений буквы
обозначается число вхождений буквы 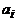 в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.
в слово. Требуется подсчитать число слов длины n, удовлетворяющих данным условиям.
| Вариант | q | n | Условие |
| 1) | n1 ?6 | ||
| 2) | n1 =2n2 | ||
| 3) | n1 + n2 < n3 + n4 | ||
| 4) | n1 = n2 + n3 + n4 | ||
| 5) | n1 = 2, n2<n3 | ||
| 6) | n1 + n2 = 3, n3 ? 2 | ||
| 7) | n1 = n2 | ||
| 8) | n1 = n2 + n3, n2 - четное | ||
| 9) | n1 + n2 < n3 | ||
| 10) | n1 + n2 = n3 | ||
| 11) | n1 < n2 | ||
| 12) | n1 + n2 ? 6 | ||
| 13) | 2 < n1 < 6 | ||
| 14) | n1 ? n2 ? n3 | ||
| 15) | n1 ?2, n2 + n3 = 4 | ||
| 16) | n1 = 4, n2 ?3 | ||
| 17) | n1 ? n2 + n3 + n4 | ||
| 18) | n1 + n2 = 3, n3 ?2 | ||
| 19) | n1 > n2 > 2 | ||
| 20) | n1 = n2 | ||
| 21) | n1 + n2 = n3 + n4 | ||
| 22) | n1 = 2, n2 ?3 | ||
| 23) | n1 ?2, n2 + n3 + n4 = 3 | ||
| 24) | n1 + n2 ?4, n3 = 1 | ||
| 25) | n1 = n2 = n3 |
19. В группе N студентов, из них 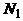 человек владеют языком программирования СИ,
человек владеют языком программирования СИ, 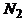 - Паскалем,
- Паскалем, 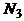 - Бейсиком,
- Бейсиком, 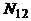 студентов программируют на СИи Паскале,
студентов программируют на СИи Паскале, 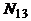 - на СИ и Бейсике,
- на СИ и Бейсике, 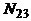 - на Паскале и Бейсике,
- на Паскале и Бейсике, 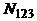 человек знают все три языка и
человек знают все три языка и 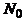 не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):
не знают ни одного из них. По данным значениям найти недостающую информацию (заполнить пустую клетку):
| Вариант | N | 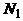 | 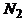 | 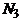 | 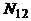 | 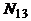 | 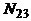 | 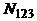 | 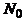 |
| 1) | |||||||||
| 2) | |||||||||
| 3) | |||||||||
| 4) | |||||||||
| 5) | |||||||||
| 6) | |||||||||
| 7) | |||||||||
| 8) | |||||||||
| 9) | |||||||||
| 10) | |||||||||
| 11) | |||||||||
| 12) | |||||||||
| 13) | |||||||||
| 14) | |||||||||
| 15) | |||||||||
| 16) | |||||||||
| 17) | |||||||||
| 18) | |||||||||
| 19) | |||||||||
| 20) | |||||||||
| 21) | |||||||||
| 22) | |||||||||
| 23) | |||||||||
| 24) | |||||||||
| 25) |
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Составители: В.Е.Алексеев, В.В.Лозин
Комбинаторика (комбинаторный анализ) – раздел дискретной математики, в котором изучаются объекты, составленные из элементов конечных множеств. Одним из основных видов комбинаторных задач являются перечислительные задачи. В этих задачах речь идет о выборе определенного количества элементов из некоторого множества с соблюдением тех или иных условий и требуется подсчитать число способов, которыми можно осуществить такой выбор.
Напомним некоторые обозначения из теории множеств.
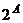 – множество всех подмножеств множества A.
– множество всех подмножеств множества A.
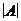 – число элементов (мощность) конечного множества A.
– число элементов (мощность) конечного множества A.
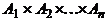 – прямое (декартово) произведение множеств
– прямое (декартово) произведение множеств 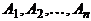 . Элементами декартова произведения являются последовательности вида
. Элементами декартова произведения являются последовательности вида 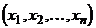 , где
, где 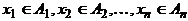 . При
. При 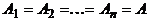 получается декартова степень
получается декартова степень 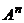 множества A. Если элементы множества A считать буквами алфавита, то элементы декартовой степени можно рассматривать как слова, они в этом случае записываются в виде
множества A. Если элементы множества A считать буквами алфавита, то элементы декартовой степени можно рассматривать как слова, они в этом случае записываются в виде 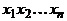 .
.
Буквой E будем обозначать двухэлементное множество 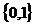 .
.
Символом отмечается конец доказательства.
Правила равенства, суммы и произведения
Очень многие комбинаторные задачи решаются применением трех простых правил, названных в заголовке.
Пусть A и B - конечные множества, f - функция, определенная на A со значениями в B. Напомним, что f называется биекцией или взаимно однозначным отображением,если выполняются условия
1) любые два различных элемента из A отображаются в различные элементы множества B (функция, удовлетворяющая этому условию, называется инъекцией);
2) для любого yÎB существует такой 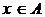 ,что
,что 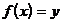 (такая функция называется сюръекцией).
(такая функция называется сюръекцией).
Если существует биекция из A в B , то говорят также, что между A и B имеется взаимно однозначное соответствие.
Правило равенства. Если между конечными множествами A и B есть взаимно однозначное соответствие, то 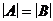 .
.
Правило суммы.Если A и B – конечные множества и 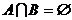 , то
, то 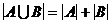 .
.
Правило произведения. Для любых конечных множеств A и B имеет место равенство 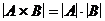 .
.
Первые два правила очевидны, третье следует из того, что при 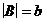 каждый элемент множества A образует b пар с различными элементами множества B, поэтому, если
каждый элемент множества A образует b пар с различными элементами множества B, поэтому, если 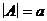 , то всего будет
, то всего будет 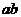 пар.
пар.
Правила суммы и произведения обобщаются на случай любого числа слагаемых или сомножителей. Для правила суммы обобщение очевидно: мощность объединения любого числа попарно непересекающихся множеств равна сумме их мощностей. Докажем обобщенное правило произведения.
Теорема 1. Для любых конечных множеств 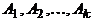 имеет место равенство
имеет место равенство 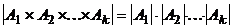 .
.
Д о к а з а т е л ь с т в о. Мы видели, что при k = 2 это справедливо. Для большего числа сомножителей доказываем индукцией по k. Элементами множества 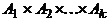 являются наборы вида
являются наборы вида 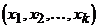 , где
, где 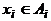 ,
, 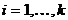 . Каждый такой набор можно рассматривать как состоящий из двух частей:
. Каждый такой набор можно рассматривать как состоящий из двух частей: 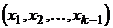 и
и 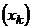 . Первая часть – элемент множества
. Первая часть – элемент множества 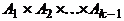 , вторая – элемент множества
, вторая – элемент множества 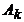 . Таким образом, имеется взаимно однозначное соответствие между множеством
. Таким образом, имеется взаимно однозначное соответствие между множеством 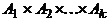 и прямым произведением двух множеств:
и прямым произведением двух множеств: 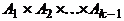 и
и 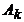 . По правилу равенства
. По правилу равенства 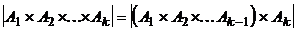 , по правилу произведения для двух сомножителей
, по правилу произведения для двух сомножителей 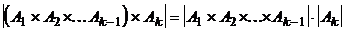 , а по предположению индукции
, а по предположению индукции 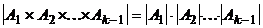 .
.
Применяя теорему 1 и правило равенства, докажем формулу для числа подмножеств конечного множества.
Теорема 2. Для любого конечного множества A имеет место равенство 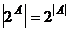 .
.
Д о к а з а т е л ь с т в о. Пусть 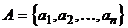 . Каждому подмножеству X множества A поставим в соответствие двоичный набор
. Каждому подмножеству X множества A поставим в соответствие двоичный набор 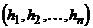 , где
, где 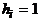 , если
, если 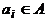 ,
, 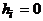 , если
, если 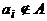 . Этот набор называют характеристическим вектором множества X. Очевидно, что по характеристическому вектору множество X можно определить однозначно. Следовательно, имеет место взаимно однозначное соответствие между
. Этот набор называют характеристическим вектором множества X. Очевидно, что по характеристическому вектору множество X можно определить однозначно. Следовательно, имеет место взаимно однозначное соответствие между 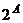 и
и 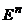 . Из правила равенства и теоремы 1 следует, что
. Из правила равенства и теоремы 1 следует, что 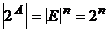 .
.
В теореме 1 речь идет о числе способов выбрать упорядоченный набор 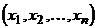 , где каждый элемент
, где каждый элемент 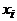 выбирается из множества
выбирается из множества 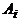 независимо от всех остальных элементов. Иногда множество, из которого выбирается
независимо от всех остальных элементов. Иногда множество, из которого выбирается 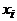 , зависит от того, какие элементы были выбраны в качестве
, зависит от того, какие элементы были выбраны в качестве 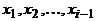 , но число элементов в этом множестве, т.е. число вариантов для выбора
, но число элементов в этом множестве, т.е. число вариантов для выбора 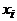 , остается постоянным. В этом случае правило произведения также применимо, но в более общей формулировке.
, остается постоянным. В этом случае правило произведения также применимо, но в более общей формулировке.
Общее правило произведения. Пусть упорядоченный набор 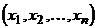 формируется в результате последовательного выбора элементов
формируется в результате последовательного выбора элементов 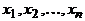 , причем для любого
, причем для любого 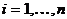 и любых
и любых 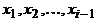 элемент
элемент 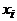 можно выбрать
можно выбрать 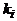 способами. Тогда весь набор может быть выбран
способами. Тогда весь набор может быть выбран 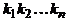 способами.
способами.
Задачи
1. Имеется 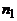 разных книг одного автора,
разных книг одного автора, 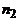 – второго и
– второго и 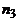 – третьего. Каким числом способов можно выбрать
– третьего. Каким числом способов можно выбрать
а) одну книгу?
б) две книги разных авторов?
в) три книги разных авторов?
2.Какимчислом способов можно заполнить анкету, содержащую n вопросов, если на каждый вопрос можно ответить
а) “да” или “нет”?
б) “да”, “нет”, “не знаю”?
3. Сколько слов длины n можно составить, если в алфавите q букв? Сколько среди них палиндромов (слов, читающихся одинаково слева направо и справа налево)?
4. Сколько матриц с m строками и n столбцами можно составить из элементов 0 и 1 ?
5.Сколько слов длины n в q–буквенном алфавите, в которых любые две соседние буквы различны?
6.Каким числом способов можно на обычной шахматной доске разместить белую и черную ладьи так, чтобы они не атаковали друг друга?
7. Сколько бинарных отношений можно определить на множестве из n элементов? Сколько среди них
а) рефлексивных?
б) симметричных?
в) антисимметричных?
Перестановки и сочетания
В простейших комбинаторных задачах требуется подсчитать число способов выбрать k элементов из n–элементного множества. То, что получается в результате выбора, называется выборкой из n по k или (n,k)–выборкой.
Понятие выборки отличается от понятия подмножества. Первое отличие состоит в том, что в выборках может допускаться повторение элементов. Это означает, что в выборку может входить несколько экземпляров одного и того же элемента. В этом случае говорят, что рассматриваются выборки с повторениями. Другое отличие – выборки могут быть упорядоченными или неупорядоченными. Упорядоченность означает, что выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, считаются различными. Если же такие выборки считаются одинаковыми, то говорят, что рассматриваются неупорядоченные выборки. Упорядоченные выборки называют перестановками (или размещениями), неупорядоченные – сочетаниями. Таким образом, имеется четыре основных типа выборок: перестановки (без повторений), перестановки с повторениями, сочетания (без повторений) и сочетания с повторениями.
Подсчитаем число выборок каждого типа. Множеством, из которого делается выбор, будем считать множество чисел 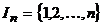 .
.
Перестановки с повторениями. Перестановки с повторениями из n по k – это последовательности длины k, состоящие из элементов множества 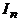 , то есть попросту элементы множества
, то есть попросту элементы множества 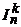 . Из теоремы 1 поэтому следует
. Из теоремы 1 поэтому следует
Теорема 3. Число (n,k)– перестановок с повторениями равно 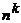 .
.
Перестановки. Обозначим число перестановок из n по k через 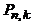 .
.
Теорема 4. 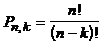 .
.
Д о к а з а т е л ь с т в о. В качестве первого элемента перестановки может быть выбран любой из n элементов множества 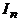 . Поскольку повторения недопустимы, второй элемент можно выбрать
. Поскольку повторения недопустимы, второй элемент можно выбрать 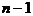 способами, третий
способами, третий 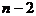 способами и т.д. Применяя обобщенное правило произведения, получаем
способами и т.д. Применяя обобщенное правило произведения, получаем
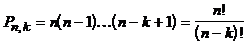 .
.
В частности, при 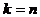 получается формула для числа перестановок всех n элементов:
получается формула для числа перестановок всех n элементов: