Сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке

İ_A + İ_B + İ_C = 0,

Симметричная нагрузка.

Z_ab = Z_bc = Z_ca = Ze^jφ

т.е. Z_ab = Z_bc = Z_ca = Z, φ_ab = φ_bc = φ_ca = φ.

Так как линейные (они же фазные) напряжения U_AB, U_BC, U_CA симметричны, то и фазные токи образуют симметричную систему

İ_ab = Ú_ab / Z_ab; İ_bc = Ú_bc / Z_bc; İ_ca = Ú_ca / Z_ca.

Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.

Линейные токи

İ_A = İ_ab - İ_ca; İ_B = İ_bc - İ_ab; İ_C = İ_ca - İ_bc;

образуют также симметричную систему токов.

На векторной диаграмме фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение U_AB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в √3 раз. Линейный ток İ_A отстает по фазе от фазного тока İ_ab на угол 30°, на этот же угол отстает İ_B от İ_bc, İ_C от İ_ca.

При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.

Фазное напряжение U_Ф = U_Л. Фазный ток I_Ф = U_Ф / Z_Ф, линейный ток I_Л = I_Ф, угол сдвига по фазе φ = arctg (X_Ф / R_Ф).

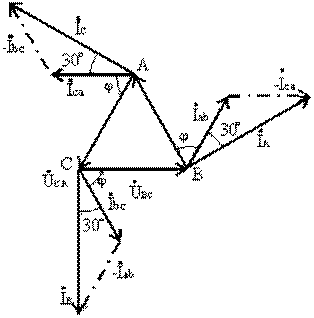
Несимметричная нагрузка приемника.

В общем случае при несимметричной нагрузке Z_ab ≠ Z_bc ≠ Z_ca. Обычно она возникает при питании от трехфазной сети однофазных приемников.

Ниже приведены векторная и топографическая диаграммы для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная.

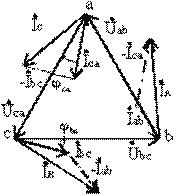
Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.

При расчете для несимметричной нагрузки сначала определяют значения фазных токов İ_ab, İ_bc, İ_ca и соответствующие им сдвиги фаз φ_ab, φ_bc, φ_ca. Затем определяют линейные токи в комплексной форме.

Необходимое оборудование и приборы.

- лабораторный стенд;

- ламповые реостаты Аx, Вy, Сz;

- амперметры А1, А2, А3, А4, А5, А6;

- вольтметр V;

- соединительные провода.

Порядок выполнения работы

1. Собрать электрическую цепь по схеме

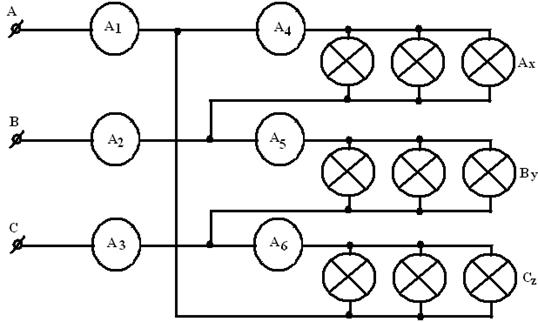
2. После проверки схемы преподавателем включить равномерную нагрузку фаз и измерить фазные и линейные напряжения и токи. Результаты измерений занести в таблицу №1.

Таблица №1

IA	IB	IC	IAB	IBC	ICA	UAB	UBC	UAC	Примечание
А	А	А	A	A	A	В	В	В
									Равномерная нагрузка фаз
									Равномерная нагрузка, оборвана линия
									Неравномерная нагрузка фаз

3. Отключить одну фазу при равномерной нагрузке фаз и измерить фазные и линейные токи и напряжения. Результаты измерений занести в таблицу №1.

4. Подключить все фазы. На ламповых реостатах создать неравномерную нагрузку и измерить фазные и линейные токи и напряжения. Результаты измерений занести в таблицу №1.

5. Построить векторные диаграммы для 1 и 3 опытов (2 диаграммы). Векторные диаграммы напряжений и токов должны быть построены в масштабе по току (например 0,1А = 1см) и напряжению (например 50 В = 1 см). Начинаем с построения векторов фазных напряжений, которые выходят из одной точки и сдвинуты в пространстве на угол 120⁰. Далее строим векторы фазных токов, совпадающих по фазе с фазными напряжениями, так как нагрузка имеет активный характер. Векторы линейных токов представляют собой разности двух фазных токов. При этом вектор разности получается, если концы двух выходящих из одной точки векторов (фазные токи) соединяются вектором (линейный ток) и стрелка ставиться к вектору, из которого вычитают.

6. Сделать вывод по работе. В выводе необходимо проверить выполнение основных соотношений для фазных и линейных токов и напряжений при соединении нагрузки треугольником по результатам замеров первого опыта. Объяснить, что произошло со схемой, когда оборвали (отключили) один из линейных проводов, и по какой причине изменились линейные токи в третьем опыте.

______________________________________________________

Оценка __________ Преподаватель ___________ ( _________________ )

19. Лабораторная работа № 19 «Измерение трёхфазной мощности двумя ваттметрами».

Цель работы:

Убедиться в возможности измерения мощности в трёхфазной цепи двумя ваттметрами при симметричной и несимметричной нагрузке.