Составить блок-схему и алгоритм табулирования функции F(x) на отрезке (А; В) с шагом ∆x.

МИНОБРНАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное

образовательное учреждение

высшего образования

«Волгоградский государственный технический университет »

ВОЛЖСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ

(филиал)

федерального государственного бюджетного образовательного учреждения высшего образования

«Волгоградский государственный технический университет»

(ВПИ (филиал) ВолгГТУ)

Автомеханический факультет

Кафедра: ВСТПМ

Задания для выполнения семестровой работы №3

по дисциплине «Информатика»

Для студентов I курса

очной формы обучения

Составитель:

к.т.н., доц. Байдакова Н.В.

Волжский 2016 г.

Пример выполнения семестровой работы№3:

Задача 1 Дано: a,b,c. Вычислить .

Если 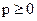вычислить 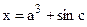. Если 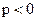вычисления закончить.

Если 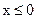вычислить и напечатать 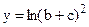. Если 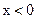найти и напечатать наибольшее из трех заданных a, b, c.

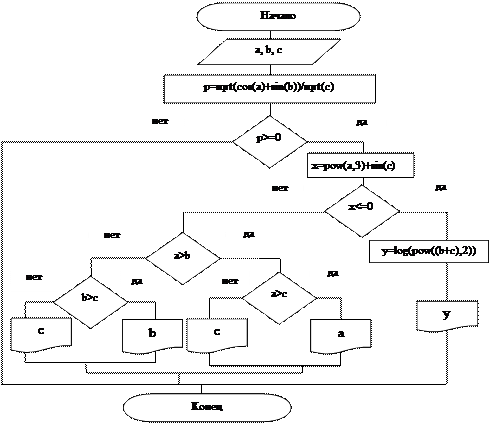
Описание блок-схемы:

Блок 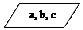включает в себя: введение с клавиатуры значения переменных.

- блок вычисления значения величины р.

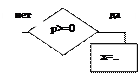- блок проверки условия. Простая форма записи. Если 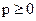вычисляем значение величины х, если 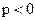, вычисления заканчиваем.

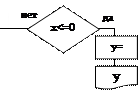
- блок проверки условия . Простая форма записи. Если 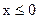вычисляем значение величины у, затем выводим это значение не экран, если 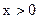, переходим к выполнению следующих действий.

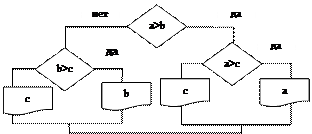-Разветвленный блок проверки условия. Осуществление поиска наибольшего из трёх значений a, b, c. Наибольшее из трёх чисел будет выведено на экран.

Задача 2 Дано: a,b.

Если 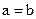вычисления закончить. Если 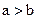напечатать « »

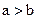Если 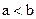вычислить .

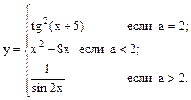где х изменяется от –1 до 3 с шагом 0,3.

Вывести на печать только отрицательные значения функции.

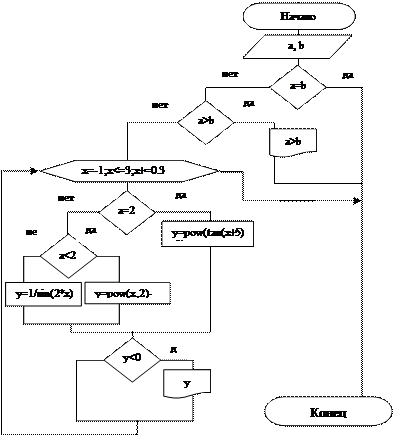
Описание блок-схемы:

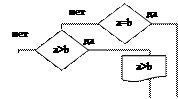
- блок введения с клавиатуры значения переменных a, b. c.

- Вложенная форма записи условия. В зависимости от значения переменной a происходит выбор линии управления: при a=b – управление передаётся на завершение алгоритма; при a>b вывод соответствующего комментария; при a < b управление передаётся на цикл:

- параметрический цикл. x – параметр цикла. Начальное значение параметра цикла равно –1, конечное равно 3, шаг равен 0.3.

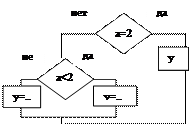В цикле выполняются следующие действия:

- блок проверки условия. Вложенная форма записи условия. В зависимости от значения переменной a вычисляется значение переменной y одним из трех способов.

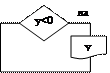
-этот блок внутри цикла гарантирует вывод на печать только отрицательных значений функции.

Задача 3: Составить программу вычисления объёма усеченного конуса по формуле: . Напечатать объём и все параметры, входящие в формулу.

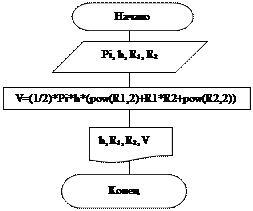
Описание блок-схемы:

- блок введения с клавиатуры значения переменных Pi, h, R₁, R₂

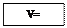- блок вычисления значения величины V.

- блок вывода на экран значение переменных h, R₁, R₂, V

ЗАДАНИЕ 1.

Составить блок-схему и алгоритм табулирования функции F(x) на отрезке (А; В) с шагом ∆x.

№вар.	ФУНКЦИЯ		А	В	∆x
	y=x2sin(x-1)/(x-1) y=(x+1)arctg e-2x y=x3+x(2+x2)	при x<1 при x=1 при x>1	-1		0,4
	y=cos2(2x+π/4) y=2tg2x-ln│cos x│ выдать сообщение «х=0» и перейти к следующей итерации цикла	при x>0 при x<0 при x=0	-π/4	π/4	π/20
	y=(1-2x)/x+3 v=x-x2 z=y+v y=ex/(1/x)1/4	при x<0 при x=0 при x>0	-2	0,5	0,25
	y=e│x│/arccosx y=sin x+cos xz=y-1 при z<0.3 закончить вычисления	при x≤0,5 при x≥0,5	0,1		0,1
	y=esinx/arccos xs=åy y=ctg x-x2 y=(x+1)ctg e-3x	при x<1 при x=1 при x>1	0,5	1,5	0,1
	y=x+(x+0,5)/(1+x ) y=lnx/arccos(x/12) y= lnx/arcsin(x/12),	при x>10 при x<10 если x=9			0,2
	y= ((ex)1/2+(ln x)1/2)/sin x z=tg 1/x y=ctg 3x-x2	при x<2 при x=2 при x>2			0,2
	z=sin x , если z>0 , то y=аrccos(x)1/2/│x│ если z<0 , то y=|sin x|1/2 y= (cos x)ex	при x≥1     при x<1			0,3
	y=аrcsin x/ln │x│ y=2tg(1/x) Если tg(1/x)<0, то выдать об этом сообщение и выйти из программы.	при │x│≤1 при │x│>1	-2		0,4
	y=arccos(1/x) y=│tg x+x3│	при 2≤x≤3 при x>3,x<2	-2		0,2
	y=arcsin(x)1/3 y=sin3 (1/x)+x2 f=x2/5	при x<1 при x =1 при x>1			0,2
	y=arccos(1/x2) y=ln(1/x) , если 1/x>3 y=lg(1/x) , если 1/x<3	при x≥1 при x<1	0,1	2,1	0,2
	y=arccos3x y=sin 1/(1+x) +x2 f=x3/(5+x)	при x<1 при x =1 при x>1	0,2		0,05
	y=аrcsin x/ln(x+5) , если |x|<1 y= x3/(x+1) , если |x|>1 y= tg3x+ln(x+5)	при │x│<1   при │x│≥1	-2		0,2
	y= (ex)1/5/tg x y=arccos x y=(1+x)/x2	при x≥1 при |x|<1 при x<-1			0,2
	y=arccos ex+x y=ln│x│ При х=0 перейти к следующей итерации без вычисления y.	при x>0 при x>0 при x =0	-2		0,2
	y=x2/(x2+2,8) z=ecos2x z=sin2x	при x>1 при 0≤x≤1 при x<1	-1		0,2
	y=ex+cos10x w=arctg((x)1/2/(x+3)) z=å yi	при x<1 при x>1 при x=1	-1		0,1
	y=cos2ex z=arctg(ln(x+2)) Вычислить s=å yi+åzi	при x<3,5 при x>3,5			0,1
20	y=ecos2x z=x2/(x2+2,8)1/2 если z<0,2 , то y=x3-x2 если z>0,2 , то y=x2-x	при x≥0 при x<0	-1		0,2
	y=arctg((x)1/2+2/x-3) z=cos x(ex) v=sin x / cos x	при x>3 при x<3 при x=3			0,3
	y=ln│tg x│ z=sin x-(x+5)1/3	при x>-5 при x≤-5	-6	-5	0,2
	y=arctg((x2+x)/3+x) z=ln(x2+3) Вычислить s=å yi+åzi	при x<-1 при x≥-1	-2	пока z<2	0,2
	y=ln│sin x+cos x│ y=cos x/sin2x Перейти к следующей итерации	при x>0 при x<0 при x=0	-1		0,2
	y=arctg e-x z= (x2-x3)1/2 Вычислить s=å yi+åzi	при x>0 при x≤0	-1		0,2
	y=x2+tgx+1 y=arcsin(x2/5) , если x2/5>0,05 и y= arccos(x2/5) , если x2/5<0,05	при x≥1 при x<1	0,1	2,1	0,2
	y=ln│tg x/2│ y= (0,5-x)4 y=cos x sin x	при x>1 при x<1 при x=1	0,5	2,5	0,1
28	y=arctg(x2+x)1/2 z=x2+(0,5x-1)4 Вычислить s=å yi+åzi	при x>0 при x≤0	-1	пока (x2+x)1/2<1,5	0,2

Задание 2.