Метод Бенгама-Мемона-Эо-Юнг

Бенгам (D. Benham), Мемон (N. Метоп), Эо (B.-L. Yeo) и Юнг (Minerva Yeung) [ЮЗ] предложили оптимизированную версию вышерассмотренного метода. Причем оптимизация была проведена ими по двум направлениям: во-первых, было предложено для встраивания использовать не все блоки, а только наиболее подходящие для этого, во-вторых, в частотной области блока для встраивания выбираются не два, а три коэффициента ДКП, что, как будет показано в дальнейшем, существенно уменьшает визуальные искажения контейнера. Рассмотрим отмеченные усовершенствования более подробно.

Пригодными для встраивания информации считаются такие блоки изображения, которые одновременно удовлетворяют следующим двум требованиям:

• блоки не должны иметь резких переходов яркости;

• блоки не должны быть слишком монотонными.

Блоки, которые не отвечают первому требованию, характеризуются наличием слишком больших значений низкочастотных коэффициентов ДКП, сопоставимых по своей величине с DC-коэффнциентом. Для блоков, которые не удовлетворяют второму требованию, характерно равенство нулю большинства высокочастотных коэффициентов. Указанные особенности являются критерием отбраковки непригодных блоков.

Отмеченные требования отбраковки учитываются использованием двух пороговых коэффициентов: P_L(для первого требования) и P_H (для второго требования), превышение (P_L) или недостижение (P_H) которых будет указывать на то, что рассматриваемый блок не пригоден для модификации в частотной области.

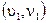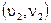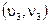Встраивание в блок бита сообщения совершается следующим образом. Выбираются (для большей стойкости стеганосистемы — псевдослучайно) три коэффициента ДКП блока из среднечастотной области с координатами , и . Еcли необходимо провести встраивание "0", эти коэффициенты изменяются таким образом (если, конечно, это необходимо), чтобы третий коэффициент сталменьше любого из первых двух; если необходимо скрыть "1", он делается большим по сравнению с первым и вторым коэффициентами:

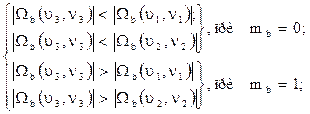(5.21)

Как и в предыдущем методе, для принятия решения о достаточности различения указанных коэффициентов ДКП, в выражение (S.21) вводится значение порога различения Р:

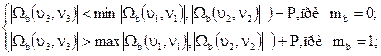(5.22)

В том случае, если такая модификация приводит к слишком большой деградации изображения, коэффициенты не изменяют, и блок в качестве контейнера не используется.

Использование трех коэффициентов вместо двух и, что самое главное, отказ от модификации блоков изображения в случае неприемлемых их искажений, уменьшает погрешности, которые вносятся сообщением. Получатель всегда может определить блоки, в которые не проводилось встраивание, просто повторив анализ, аналогичный выполненному на передающей стороне.

Приведем возможный вариант реализации данного метода в программе MathCAD.

Шаг1

Исходные данные, программные модули разбития массива контейнера на блоки и проведение операции прямого ДКП аналогичны использованным при моделировании предыдущего метода ((М.45ММ.47)).

Шаг 2

Зададим координаты трех коэффициентов ДКП в массиве 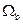, которые будем использовать для встраивания и извлечения битов сообщения р/из контейнера. Например,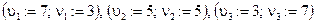

Устанавливаем значения порогов отбраковки блоков. Пусть Р_L:=2600, а Р_H:= 40. Также задаем порог различения Р:= 50.

Шаг 3

Встраивание сообщения М в блоки контейнера будем выполнять, используя программный модуль (М.52).

В начале вычисления массиву присваивается значение немодифицированного массива коэффициентов ДКП для всех блоков изображения — 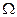. После преобразования формата сообщения из строки символов в вектор двоичных данных размерностью 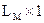происходит непосредственно модификация оптимальных для встраивания блоков.

Переменная-счетчик w перед началом цикла перебора элементов вектора M_{vec_bin} принимает нулевое значение. В начале цикла совершается проверка условия невыхода переменной 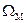за границы общего количества сегментов N_C. В случае, если w>N_C, цикл прерывается после присвоения переменной Пи строки символов, которая информирует отправителя о количестве встроенных бит (при текущих значениях порогов P_Lи Р_H) и рекомендует расширить границы (то есть увеличить значения Р_Lи/ или уменьшить Рн), что приведет к увеличению количества блоков, которые будут отвечать поставленном требованиям.

Разумеется, расширение границ приведет к появлению в списке блоков, выбранных для встраивания, которые будут не вполне оптимальны для данной операции. Поэтому в процессе договоренности между сторонами скрытого обмена относительно алгоритма псевдослучайного выбора трех пар координат коэффициентов ДКП и значений порогов отбраковки обязательно должна присутствовать фаза проверки выбранного в качестве контейнера изображения (набора изображений) на достаточность его пропускной способности. Другими словами, после установления определенных значений порогов P_L и Р_H. вычисляется количество блоков, признанных пригодными для встраивания, и выполняется оценка визуального искажения контейнера. По полученным результатам принимается решение о достаточности выбранных значений порогов или же о необходимости их изменения.

Например, установленные выше параметры позволяют признать пригодными. Для встраивания 201 блок в выбранном нами контейнере. Приведем результаты вычисления количества пригодных блоков 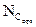в зависимости от параметров P_L и Р_H (рис. 5.29).

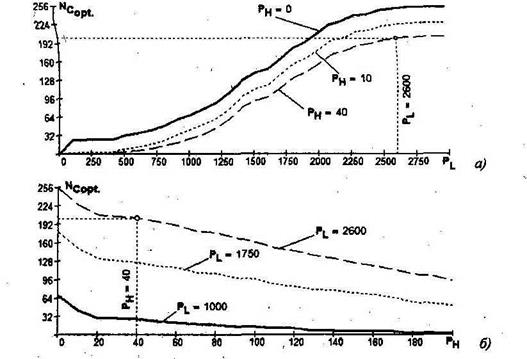
Рис. 5.29. Зависимость количества пригодных для встраивания блоков от значений порогов P_L и Р_H: P_L=var, Р_H=const(a); Р_L=const, Р_H=const(б)

Циклом изменения параметра с в модуле (М.52) совершается выбор матрицы коэффициентов ДКП для с-го блока. Для выбранной матрицы подсчитывается сумма Модулей коэффициентов, которые отвечают низкочастотному 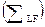и высокочастотному 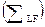участкам массива 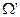(см. рис. 5.27). Не учитывается только DC-коэффициент (условие 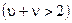). Если значения полученных сумм удовлетворяют поставленным требованиям, переменной w присваивается номер блока, признанного пригодным для встраивания, и цикл изменения с прерывается.

Проводится считывание коэффициентов массива 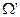(на котором произошла остановка), которые отвечают координатам 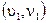, 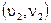и 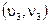. Если третий коэффициент не отвечает требованиям (5.22), проводится модификация двух коэффициентов из трех — собственно третьего коэффициента и коэффициента, который более всего отличается от третьего. Изменение происходит таким образом, чтобы разница между данными коэффициентами равнялась порогу различения Р. Возможна и односторонняя модификация одного лишь третьего коэффициента (дополнительно изображено в листинге для модуля (М.52)), однако в этом случае нарушения структуры изображения будут более значительными.

Модифицированные значения коэффициентов заменяют соответствующие по координатам значения в массиве , который, в свою очередь, присваивается w-му элементу результирующего массива .

Шаг 4

Используя модуль (М.53), проводим обратное дискретно-косинусное преобразование.

При этом, как и в предварительно рассмотренном методе, необходимо учесть возможность выхода значении интенсивностей пикселей за допустимые границы. Нормирование, аналогичное использованному в (M.50), нецелесообразно по причине того, что будет нормироваться весь массив контейнера и при извлечении возрастет вероятность ошибочного отбраковывания блоков, в которые передающей стороной было произведено встраивание бит информации (ошибка второго рода), Вследствие этого предлагается провести нормирование непосредственно результатов обратного ДКП отдельных блоков, а именно таких, у которых максимальное абсолютное значение любого элемента превышает 255. В противном случае элементам блока контейнера возвращается только их абсолютное значение.

Шаг 5

Формирование на основе блоков общего изображения выполняется программным модулем (М.50), однако уже без нормирования значений элементов контейнера на завершающем этапе.

Графическое представление восстановленного массива синей составляющей при указанных выше начальных данных приведено на рис. 5.30, а. На рис. 5.30, б представлен вид, который приобретает данный массив в случае установления значения порога различения Р:= 350 при неизменных прочих значениях (модифицируются один из первых двух коэффициентов и третий). На рис. 5.30, в изображен результат односторонней модификации третьего коэффициента ДКП (см. (М.52)) при неизменных прочих данных.

Сравнение рис. 5.30 и рис. 5.28 приводит к очевидному выводу о преимуществе метода Бенгама и др. над методом Коха и Жао, поскольку первый позволяет эффективно отобрать именно те блоки изображения, встраивание в которые будет наименее заметным. Однако пропускная способность стеганосистем, построенных на основе рассматриваемого метода, будет уступать данному показателю систем, в основу работы которых заложен метод Коха и Жао.

Рис. 5.30. Результаты встраивания сообщения М в массив канала синего при выборе оптимальных для встраивания блоков на основе разных значений порога Р и при различных алгоритмах модификации коэффициентов ДКП

Шаг 6

В процессе извлечения повторяется анализ блоков, аналогичный выполненному на этапе встраивания сообщения в контейнер.

Предварительно должны быть известными: алгоритм скрытия, массив-контейнер (В*) и его размерность (X*, Y*), размерность сегментов (N*) и координаты коэффициентов ДКП, которые использовались во время скрытия (или алгоритм их получения): 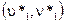, 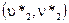и .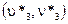

Проводится вычисление общего количества сегментов в изображении-контейнере — N*_c.

Разбивка массива В* на сегменты С*_b выполняется программным модулем (М.45). К каждому сегменту применяется прямое ДКП (М.46) и (М.47), результатом чего является массив коэффициентов ДКП сегментов C*_c

Извлечение скрытой информации совершается программным модулем (М.54), в основу которого положена проверка блока на его пригодность к встраиванию.

По результатам проверки в (M.54) делается вывод о том, был ли выбран рассматриваемый блок передающей стороной в качестве контейнера для бита сообщения, или же он был отбракован как не отвечающий требованиям пригодности. При положительном решении выполняется проверка соотношений (5.21), по результатам которой формируется вектор двоичных данных, преобразующийся в дальнейшем в символьную строку (аналогично тому, как это было реализовано в (М.5 1)).

Результаты вычисления показателей визуального искажения при Р=1 и Р=35 сведены в табл. 5.4 (стр. 179).

Метод Хсу и By

Хсу (Chiou-Ting Hsu) и By (Ja-Ling Wu) [104] был предложен алгоритм встраивания цифрового водяного знака в массив коэффициентов ДКП блоков изображения-контейнера. Приведем основные положения, заложенные авторами в основу алгоритма.

Пусть С — полутоновое изображение размером , a W — ЦВЗ, который представляет собой двоичное изображение размером 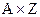. В ЦВЗ пиксель может принимать значение или «1», или «0». Разумеется, что непосредственное наблюдение такого изображения невозможно, поскольку интенсивности 0 и 1 отвечают черному цвету (последняя — в некотором приближении). Изображение ЦВЗ можно создать черно-белым, а перед скрытием заменить интенсивность белых пикселей (255) на единицу, например, путем деления всего массива ЦВЗ на 255. При извлечении, наоборот, для визуального наблюдения массив ЦВЗ необходимо умножить на 255.

Поскольку, как будет показано в дальнейшем, во время встраивания ЦВЗ будет обрабатываться только среднечастотный диапазон сигнала-контейнера, необходимым предусловием является то, что ЦВЗ должен иметь меньший по сравнению с контейнером размер. Так, например, для контейнера, разбитого на блоки 8x8, при встраивании ЦВЗ оптимальным будет использование 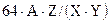коэффициентов ДКП. Отношение 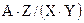в данном случае определяет то количество информации, которое может быть встроено в выбранное в качестве контейнера изображение (в приведенном примере — до 64 коэффициентов блока 8x8). Для большей стойкости и скрытости результатов использования рассматриваемого стеганометода количество встроенной информации на практике пытаются уменьшить.

Изображение-контейнер С и ЦВЗ W представим как

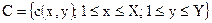(5.23)

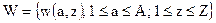(5.24)

где 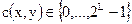— интенсивность пикселя (х,у); L — количество бит, которое используется для квантования интенсивностей; 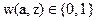— двоичные значения пикселя (a, z) ЦВЗ.

Контейнер С можно разбить на 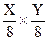блоков размерностью 8x8. Для получения этого же количества блоков, ЦВЗ разбивается на блоки размерностью 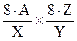. Например, если А=Х/2 и Z= Y/2, размерность блока ЦВЗ составит 4x4; если же А= Х/4 и Z = Y/4, — 2x2 и т.д.

Для создания контейнера или ЦВЗ необходимой размерности, к последним могут быть добавлены дополнительные столбцы или строки.