Математическое моделирование

СОЛИТОНОВ НА ДНК

Марио Салерно первым начал компьютерное экспериментирование с солитонами на ДНК не только как с формальными математическими структурами, он попытался связать их поведение в одномерном прост-ранстве полинуклеотидов с их биогенетическими, а точнее, с эпиге-нетическими функциями[18]. При этом он развил первую модель солитонов на ДНК, предложенную Инглендером и соавторами[19]. Эта модель и в последующем ее более детальные формы, включая нашу (см. ниже), представлена в понятиях механических систем как цепочка осцилляторов (оснований ДНК), связанных упругими нелинейными сахаро-фосфатными связями. Вслед за Салерно основное внимание мы уделили реально существующим известным последовательностям ДНК и влиянию их на характер поведения солитонов. На первом этапе мы повторили его эксперименты, но на существенно более длинных отрезках ДНК. Действительно, солитонные возбуждения типа кинков чувствительны к месту своей инициации, и продвижение их вдоль одной из цепочек ДНК, когда они раскрыты вследствие тепловых флуктуаций, сопровождается специфической модуляцией траектории кинков во времени. Такие солитоны являются структурами, излучающими электромагнитное и акустическое поле, их внутренняя колебательная структура способна отобразить и ретранслировать тексты и иные знаковые структуры ДНК во внутри- и внеклеточное пространство, по крайней мере на уровне крупных блоков последовательностей. В качестве примера можно привести поведение кинка на фрагменте ДНК длиной 1020 пар оснований из вируса саркомы птиц.

C-район ДНК (1 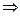1020 нуклеотид) на 3’-конце вируса саркомы птиц. Содержит несколько “семантически” определенных участков, таких, как полипептид-кодирующий участок (между 558 и 675 нуклеотидами); PolA (936)  3’-конец вирусной РНК, сайт поли-аденилирования; 916 нуклеотид  5’-конец вирусной РНК (“capping site”); Red-участок ()  короткий концевой повтор вирусного генома; Pro  вероятный компонент промотора транскрипции (между 870 и 900); палиндром-”шпилька” (870 912)[20].

(5’ начало) 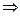GGC CTA TGT GGA GAG GAT GAA CTA CGT GCA CCG AGA CCT GCG GGC GGC CAA CAT CCT GGT GGG GGA GAA CCT GGT GTG CAA GGT GGC TGA CTT TGG GCT GGC ACG CCT CAT CGA GGA CAA CGA GTA CAC AGC ACG GCA AGG TGC AAG TTC CCC ATC AAG TGG AGA GCC CCC GAG GCA GCC CTC TAT GGC CGG TTC ACC ATC AAG TCG GAT GTC TGG TCC TTC GGC ATC CTG CTG ACT GAG CTG ACC ACC AAG GGC CGG GTG CCA TAC CCA GGG ATG GGC AAC GGG GAG GTG CTG GAC CGG GTG GAG AGG GGC TAC CGC ATG CCC TGC CCG CCC GAG TGC CCC GAG TCG CTG CAT GAC CTT ATG TGC CAG TGC TGG CGG AGG GAC CCT GGA GGA GCG GCC CAC TTT TCG AGC TAC CTG CAG GCC CAG CTG CTC CCT GCT TGT GTG TTG GAG GTC GCT GAG TAG TGC GCG AGT AAA ATT TAA GCT ACA ACA AGG CAA GGC TTG ACC GAC AAT TGC ATG AAG AAT CTG CTT AGG GTT AGG CGT TTT GCG CTG CTT CGC GAT GTA CGGGCC AGA TAT ACG CGT ATC TGA GGG GAC TAG GGT GTG TTT AGG CGA AAA GCG GGG CTT CGG TTG TAC GCG GTT AGG AGT CCC CTC AGG ATA TAG TAG TTT CGC TTT TGC ATA GGG AGG GGG AAA TGT AGT CTT ATG CAA TAC TCT TGT AGT CTT GCA ACA TGG TAA CGA TGA GTT AGC AAC ATA CCT TAC AAG GAG AGA AAA AGC ACC GTG CAT GCC GAT TGG TGG AAG TAA GGT GTA CGA TCG TGC CTT ATT AGG AAG GCA ACA GAC CGG GTC TGA CAT GGA TTG GAC GAA CCA CTG AAT TCC GCA TCG CAG AGA TAT TGT ATT TAA GTG CCT AGC TCG ATA CAA TAA ACG CCA TTT GAC CAT TCA CCA CAT TGG TGT GCA CCT GGG TTG ATG GCT GGA CCG TCG ATT CCC TAA CGA TTG CGA ACA CCT GAA TGA AGC AGA AGG CTT CATT 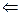1020 (3’-конец)

На рис.1 и рис. 2 кинки имеют форму пиков “горных гряд”, а не ступенек, поскольку взята производная от функции уравнения синусГордона. Здесь горизонтальная ось  последовательность ДНК, верти-кальная  амплитуда солитона. Ось на зрителя  время. Видно, как при изменении места инициации солитона на определенных последо-вательностях полинуклеотида заметно меняется динамика этой уеди-ненной волны в форме ее колебательных движений вдоль цепочки ДНК.

Исследуемый район молекулы богат функционально (и семантически) биологически значимыми участками, и мы вправе ожидать, что они, эти участки, будут изменять, модулировать, то есть вводить ДНК “текстовую” информацию в солитонную волну как в переносчик генетических сообщений. Такая модуляция колебательной структуры солитонов отчетливо наблюдается на приведенных графиках. Можно полагать, что спектральный состав частот колебаний солитонов является одним из механизмов преобразования текстовых структур ДНК и РНК в волновую форму и средством передачи генетических и иных сообщений в одномерном пространстве вдоль цепочек полинуклеотидов и (или) в трехмерном измерении генома как отдельной клетки, так и тканевого континуума биосистемы.

400-ый

Рис.1

Влияние нуклеотидной последовательности ДНК на динамику конфор-мационного возмущения уединенной (солитоноподобной ) волны. Последо-вательность нуклеотидов - вирус саркомы птиц (первые 600 пар оснований). Центр возмущения - 400-ый нуклеотид.

450-ый

Рис.2

То же, что на рис.1, но центр возмущения цепочки ДНК на 450-ом нуклеотиде.

Так работает компьютерная модель динамики солитонов, в определенной мере развитая Салерно после ее выдвижения Инглендером. Салерно дал формализм, описывающий вращательные колебания нуклеотидов молекулы ДНК, для того чтобы объяснить экспериментальные данные по водородно-тритиевому обмену в ДНК. Согласно этой модели по Инглендеру, в цепи ДНК могут возникать (под воздействием теплового шума) и распространяться открытые состояния (“плавление” двойной спи-рали ДНК на коротких участках, обогащенных АТ-парами ) в виде локализованных дислокаций ( уединенных волн). Марио Салерно, про- должая работу Инглендера, в упрощенном варианте выявил влияние последовательности нуклеотидов на нелинейную динамику вращательных колебаний нуклеотидов на однотяжных участках ДНК, образующих такие открытые (“open state”) области. Позднее Якушевич, Федянин, Хомма и др. рассмотрели различные обобщения модели Инглендера, с оценкой особенностей строения ДНК, учитывая обрыв водородной связи при открытии оснований, парность цепи ДНК и другие степени свободы, отличные от вращательных. Однако, в указанных работах недостаточно сказано о причинах возникновения дислокаций в ДНК. Мы предлагаем возможный механизм этого процесса в ДНК, альтернативный гипотезе Инглендера о воздействии теплового шума как причины раскрытия пар оснований. Мы считаем, что дислокации на ДНК могут возникать при изменении периода спирали ДНК (основная часть идеи принадлежит М.Ю.Маслову).

В нашей модели нуклеотиды ДНК рассматриваются как осцилляторы, подвешенные на невесомом нерастяжимом стержне; сахаро-фосфатная связь между соседними нуклеотидами в цепи моделируется линейными пружинами; спирализация вдоль цепи не учитывается; водородные связи между комплементарными основаниями моделируется “гравитационным” потенциалом. Гамильтониан по М. Салерно выглядит следующим образом: 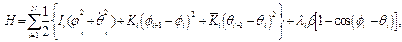(1)

где: 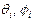 углы вращений нуклеотидов в разных цепях, 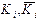 константы упругости вдоль цепей, 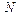 число пар в цепи, 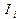 момент инерции оснований, 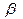 константа упругости водородных связей между комплементарными основаниями.

Коэффициенты 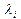в уравнении (1) определяются в соответствии с правилом: 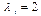в случае АТ и ТА пар, 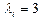в случае ГЦ и ЦГ пар; 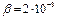 параметр, определенный Федяниным и Якушевич[21] и полученный на основе модели синус-Гордона и экспериментальных данных. Далее для упрощения модели считается, что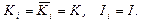

Уравнения движения для разности 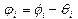, полученные из (1), имеют по М. Салерно вид:

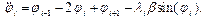(2)

где произведена замена .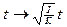

В случае 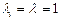, в системе (2) можно перейти к безразмерному дифференциальному уравнению синус-Гордона:

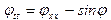, (3)

”непрерывный аналог” системы (2). Это уравнение имеет солитонные решения, в частности, односолитонное решение, или кинк, соответствует дислокации в цепи.

Основным предположением моделей ИнглендераСалерно является то, что взаимодействие между комплементарными основаниями описывается потенциалом 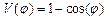(4), в котором не учитывается обрыв водородной связи.

В нашей работе рассматривается следующий потенциал :

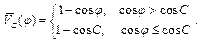
Кроме того, учитывается вязкость водной среды (в воде вязкость 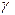~ 1).

Рассматриваются также факторы, приводящие к спирализации ДНК, при этом они считаются внешними силами, задаваемыми потенциалом

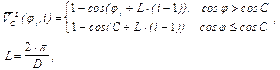
где 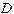 период спирали.

Уравнения (2) с потенциалом 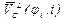и с учетом вязкости принимают вид:

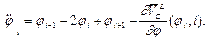(5)

Известно, что период спирали ДНК меняется в зависимости от влажности. В частности, для кристаллической ДНК 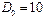, а в водной среде 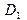 в пределах от 10. 3 до 10. 6. Именно этим фактором обусловлено явление суперспирализации. При изменении шага спирали в цепи ДНК (с фиксированными или замкнутыми концами) возникает напряжение, связанное с недостатком (избытком) количества витков спирали до релаксированного состояния. Если 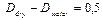, то при переходе из сухого в увлажненное состояние для цепи длиной в 300 пар оснований возникнет избыток в 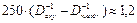витка.

В нашей работе на основе результатов численного моделирования, представленных ниже, выдвигается следующая гипотеза: изменение шага спирали может привести не только к суперспирализации, но и к локальному распариванию цепи ДНК. Кроме того, при суперспирализации напряжение в цепи снимается не полностью, поэтому локальное распаривание, вероятно, может происходить и одновременно с суперспирализацией.

Система (5) численно интегрировалась в интервале 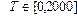с шагом 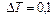. Начальные условия следующие:

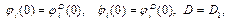
Период спирали в системе (5) 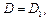длина poly(A)-цепи - 300 пар оснований. То есть параметры периода спирали в начальных условиях и в системе (5) различны. Таким образом смоделирован перенос ДНК из кристаллического состояния в увлажненное.

Граничные условия следующие (назовем их “квазициклическими”):

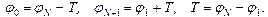
Особенностью данной модели является то, что при переходе из состояния с периодом в 10 пар в состояние с периодом в 10, 5 пар почти вся цепь оказывается денатурированной (“расплавленной”). Приведенные ниже результаты описывают процесс ренатурации такой цепи с возникновением дислокаций.

В этих экспериментах варьировались параметры: 1) диссипация 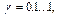2) отношение параметров упругости 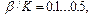3) угол обрыва водородных связей .

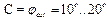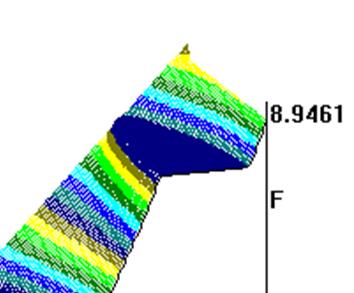
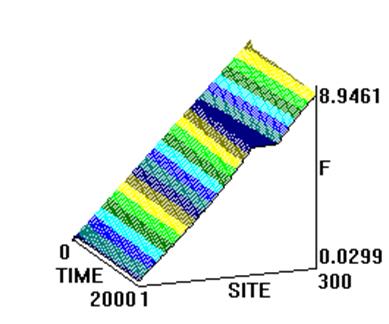
На рис. 3 и 4 представлены результаты численного интегрирования системы (5). Показана не сама функция 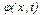, а разница 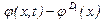, поскольку область изменения функции 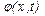(приблизительно от 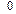до 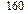) велика по сравнению с характерными изменениями в системе (приблизительно от 0 до 9). Горизонтальная часть графиков соответствует нераспаренному участку цепи с периодом спирали 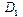. Наклонная часть графиков на рис. 3(a), 4(а) соответствует дислокации.

Можно сделать следующие выводы:

1) Способность к образованию дислокации в этой модели сильно зависит от 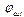. При 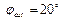дислокация возникла во всех рассмот-ренных случаях.

2) Способность к образованию дислокации также сильно зависит от параметра 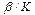. Во всех случаях, когда параметр 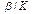велик (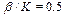

на рис. 1.а, 2.а ), дислокация возникла. В пользу этого утверждения также свидетельствует сравнение рис. 3(а) и 4(г).

Как показывают дополнительные расчеты, влияние 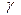на эффект проявляется в меньшей степени. Дислокация образуется или не образуется вне зависимости от значения 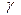( 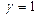или 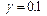). При больших значениях 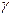дислокация образуется медленнее, чем при меньших.

3) На рис. 3(а), 4(в,г) видно, что дислокация имеет кинкообразную форму.

Ширина дислокации зависит от параметров 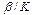(чем больше 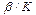, тем меньше ширина дислокации) и 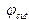(чем больше 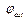, тем меньше ширина дислокации).

Развивая дальше модели солитонных возбуждений в ДНК (совместно с М.Ю.Масловым и др.) мы использовали условия, при которых цепочки ДНК моделируются набором ровибронных осцилляторов, подвешенных на невесомом нерастяжимом стержне; для простоты спирализация цепи не учитывается, а ровибронные степени свободы одной из цепочек считаются “замороженными”.

В этом случае гамильтониан для “активной” цепочки записывается в следующем виде:

H=H₀+H₁+H₂

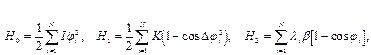(1)

где: 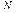- число пар оснований в цепи; 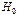- гамильтониан, описывающий собственные осцилляции мономеров ( 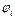- углы вращения нуклеотидов в цепочке, 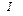- момент инерции оснований); 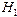- гамильтониан , характеризующий нелинейно-периодическую связь между осцилляторами ( 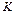- константа упругости цепочки, 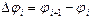), 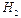- гамильтониан,

(а)

(б)

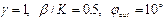а) б)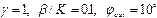

а)x0=200 б)x0=250

Рис.3

в) г)

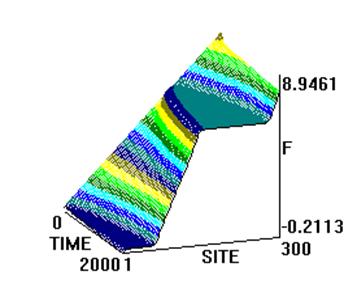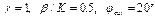в) г)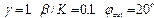

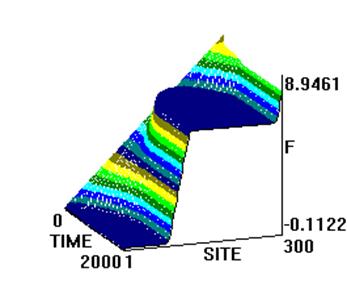
в) x0=300 г) x0=350

Рис. 4

описывающий нелинейную связь между “активной” и “замороженной” ( 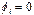) цепочками ДНК ( 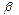- константа упругости водородных связей между комплементарными основаниями, коэффициенты 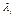в уравнении (1) определяются в соответствии с правилом: 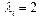в случае АТ и ТА пар, 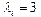в случае ГЦ и ЦГ пар; 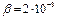- параметр, полученный ранее (см. выше) и определяемый на основе модели синус-Гордона).

При малых 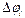гамильтониан 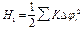, что совпадает с соответствующей частью общего гамильтониана, использованного ранее (см. выше). В этом случае уравнения движения для 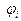, полученные из (1),

имеют вид:

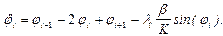(2)

где произведена замена .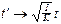

В случае 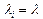в системе (2) можно перейти к безразмерному дифференциальному уравнению синус-Гордона:

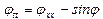, (3)

”непрерывный аналог” системы (2). Это уравнение имеет солитонные решения, в частности, односолитонное решение, или кинк, характеризующий динамику распространения дислокации в цепи.

В соответствии с (1) система нелинейных уравнений движения записывается следующим образом:

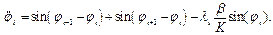(4)

Как видим, системы (2) и (4) существенно различаются. Отметим, однако, что проведенное нами численное моделирование динамики систем (2) и (4) показало следующее: если в качестве начальных условий для численного интегрирования (2) выбрать односолитонное решение его “непрерывного аналога” (3) - кинк (см. выше), то обнаруживается принципиальное сходство в характере решений.

Однако, при задании начальных условий в следующем виде:

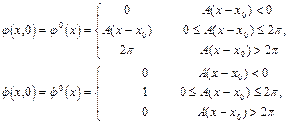(5)

где 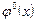-”ступенчатая” функция с высотой ступени 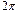и углом наклонауступа A, выявилось различие динамики данных систем (срав. рис.1 и 2,3). Более точно, системы (2) и (4) численно интегрировались методом Рунге-Кутта четвертого порядка с начальными условиями, заданными в виде (7), в интервале 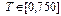с шагом 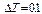. Граничные условия - “квази-циклические”:

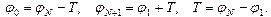
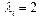(поли-A-последовательность). Параметр системы 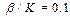. Варьировался параметр A (угол наклона уступа функции ).

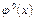Численное интегрирование системы (2) ( рис. 1) показало, что образуются две уединенных волны, движущихся справа налево по цепи с постоянной скоростью. Первая волна имеет форму квазикинка, а вторая волна имеет форму квазибризера, причем скорость первой волны превосходит таковую для второй. Обе волны за счет “квазициклических” граничных условий, доходя до левого конца, появляются на правом конце без изменения своей формы. Квазикинк, проходя по цепи маятников, изменяет координату каждого маятника на угол 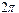(маятник делает полный оборот). Поэтому, проходя по замкнутой цепи маятников К раз, он изменяет координату каждого маятника на угол 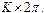Этим объясняется “уступообразная” форма графика на рис. 1.

На рис. 2 представлены результаты интегрирования системы (4) при тех же условиях. Из рисунка видно, что образуются те же две уединенных волны - квазикинк и квазибризер. Но принципиальное отличие от рассмотренного случая состоит в том, что квазикинк в самом начале движется с отрицательным ускорением, так что в результате его скорость оказывается меньше скорости квазибризера. Заметим, что исследования проводились на однородной поли-A-последовательности; так что изменение скорости квазикинка нельзя объяснить влиянием неоднородности цепочки. Этот эффект объясняется нелинейным взаимодействием между ее мономерами.

Рис. 3 иллюстрирует результаты интегрирования системы (4) при тех же условиях за исключением того, что A=2. В данном случае реализуется только квазикинк и его отрицательное ускорение в начале движения таково, что в результате он движется в направлении, противоположном первоначальному. При интегрировании системы (2) в аналогичных условиях также образуется только квазикинк. Его скорость не меняется по сравнению со случаем рис. 1.

Существенно, что при соответствующих условиях в системе типа ДНК или РНК могут возникнуть перевзбужденные ровибронные состояния. На квантовом языке это было бы адекватно перезаселению высоко лежащих квантовых уровней по сравнению с основным (реализации инверсной заселенности). В этом случае возникает заманчивая мысль, связанная с принципиальной возможностью создания биосолитонного лазера (БСЛ) на молекулах ДНК[22].

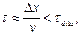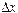Однако, в теории динамики биополимеров хорошо известно, что конформационные движения реализуются по механизму ограниченной диффузии ввиду сильного влияния диссипативных сил со стороны микроокружения. По этой причине решение проблемы создания БСЛ на ДНК представляется весьма проблематичным, по крайней мере, для подтверждения идеи необходимо выполнение условий: где и 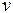‑ ширина и скорость солитона соответственно, 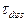‑ время диссипации. Положив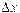 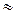5A и 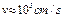(скорость звука), имеем оценку 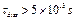. Отметим, что характерное время диссипации за счёт водных гидродинамических сил 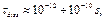а время затухания, обусловливаемое процессами внутри самой молекулы 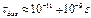(см., напр., Шайтан К.В. Биофизика. М.,1994. Т.39. С.949.; Чернавский и др. 1986. № 287. С. 21.).

Существует также и другая сложность в отношении самосогласования биосолитонов и волны электромагнитного переизлучения. Напомним, что математическое моделирование в данном случае проводилось на монотонной поли-A ДНК и поэтому оставалось неясным влияет ли гетерогенная естественная последовательность ДНК на динамику солитонного возбуждения в молекуле. Чтобы проверить это, как и ранее, был взят С-район ДНК на 3’-конце вируса саркомы птиц в качестве полигона для запуска солитонов на разных участках полимера. На этот раз вычисляли производную от функции с тем, чтобы нагляднее показать движения солитонов.

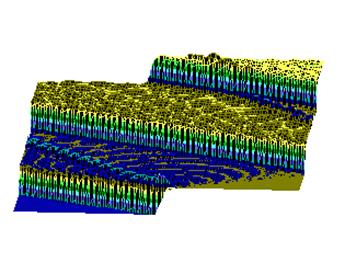
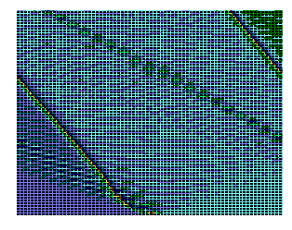
На рис.5,6 (см. ниже) хорошо видно, как при сдвиге области возбуждения солитонной волны от правой нижней части графика налево траектория волны претерпевает существенные изменения, т.е. “словесно-речевое” наполнение ДНК отображается в поведении солитона. Но главное здесь не только и не столько в этом. На этот раз характерно не качание волны около некоторого положения равновесия, а движение ее в левую часть цепочки после определенного временного интервала. В этом видится определенный биологический смысл. Солитон как потенциальный “субъект чтения” ДНК должен “просматривать” протяженные контекстные зоны, а не застревать на одних и тех же “словах”.

а) б)

Рис.5

а) Результаты численного моделирования динамики распространения возмущений в ДНК на основе системы (2) при значении параметра A=1.

б) То же, вид сверху.

а)

б)

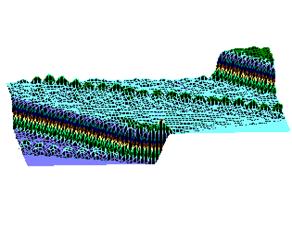
Рис.6

а) Результаты численного моделирования динамики распространения возмущений в ДНК на основе системы (4) при значении параметра A=1.

б) То же, вид сверху.

a)

б)

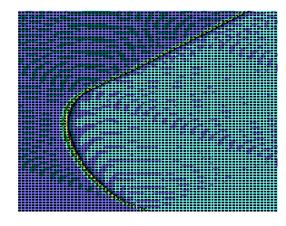
Рис.7

а) Результаты численного моделирования динамики распространения возмущений в ДНК на основе системы (4) при значении параметра A=2.

б) То же, вид сверху.

200-ый

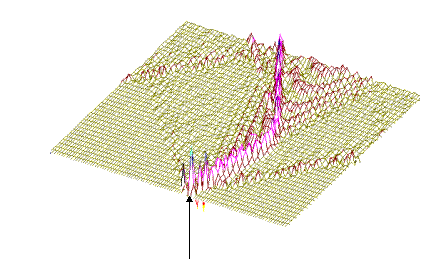
Рис.8

Солитонное возбуждение ДНК, но с учётом нелинейности ковалентных связей в сахаро-фосфатном остове ДНК. Последовательность нуклеотидов - вирус саркомы птиц (первые 600 пар оснований). Центр возмущения - 200-ый нуклеотид.

400-ый

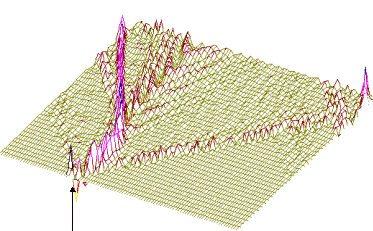
Рис.9

То же, что на рис. 8, но центр возмущения - 400-ый нуклеотид.

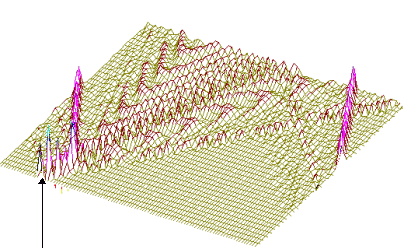
500-ый

Рис.10

То же, что на рис. 9, но центр возмущения - 500-ый нуклеотид.