Пример расчета минимума функции методом сопряженных направлений

Рассмотрим задачу минимизации функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)² из начальной точки Х⁽¹⁾ = [2.5 2.5]^Т.

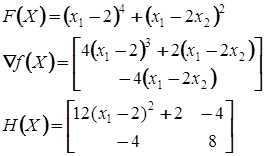
Выберем произвольное начальное единичное направление 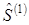= [0,87 ‑ 0,50] и определим длину шага

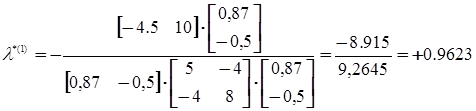
Тогда .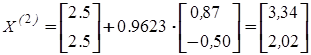

Следующее направление 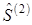выбираем сопряженным к 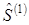. Для этого используем два уравнения: сопряженности и единичной нормировки.

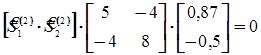
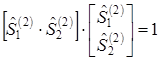
Из этих уравнений следует, что

,

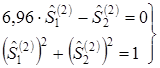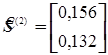
Далее определяем l^*(2)

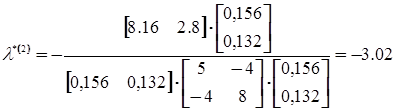
и находим следующую точку

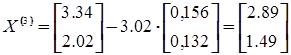
Результаты полного расчета методом сопряженных направлений представлены в таблице 2.9. Траектория поиска приведена на рис. 2.9.

Таблица 2.9

Расчет минимума функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)² методом сопряженных направлений.

№	x1	x2	f(Х)	f'(x1)	f'(x2)	f'’(x1)	f'’(x1,x2)	f'’(x2)	s1	s2	λ	ε
	2.500	2.500	6.313	-4.500	10.000	5.000	-4.000	8.000	0.870	-0.500	-0.9623	10.965
	3.337	2.019	3.688	8.163	2.802	23.457	-4.000	8.000	0.156	0.132	3.0210	8.6303
	2.867	1.620	0.704	1.864	1.490	11.025	-4.000	8.000	0.305	-2.193	-0.0602	2.3863
	2.886	1.488	0.623	2.598	0.361	11.411	-4.000	8.000	0.082	0.053	3.5974	2.6226
	2.590	1.297	0.121	0.815	0.014	6.180	-4.000	8.000	0.810	-6.086	0.0017	0.8153
	2.589	1.307	0.121	0.766	0.102	6.160	-4.000	8.000	0.034	0.019	5.7630	0.7723
	2.393	1.196	0.024	0.242	0.000	3.849	-4.000	8.000	0.991	-7.413	0.0005	0.2422
	2.392	1.200	0.024	0.226	0.030	3.845	-4.000	8.000	0.030	0.016	4.3759	0.2280
	2.261	1.131	0.005	0.071	0.000	2.820	-4.000	8.000	0.999	-7.449	0.0001	0.0715
	2.261	1.132	0.005	0.067	0.009	2.819	-4.000	8.000	0.031	0.016	2.8411	0.0674
	2.174	1.087	0.001	0.021	0.000	2.364	-4.000	8.000	1.000	-7.448	0.0000	0.0211
	2.174	1.087	0.001	0.020	0.003	2.364	-4.000	8.000	0.031	0.016	1.8672	0.0200
	2.116	1.058	0.000	0.006	0.000	2.162	-4.000	8.000	1.000	-7.446	0.0000	0.0063

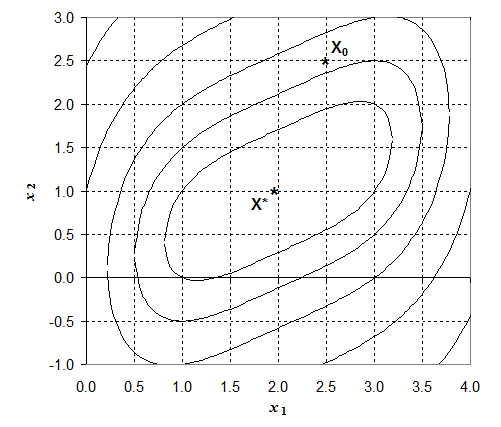Рис.2.9 Графическая иллюстрация поиска минимума методом сопряженных направлений.

3. ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.

Выполнение заданий предусматривает:

- для заданной функции поиск экстремума аналитически и его анализ;

- построение линий уровня;

- поиск минимума функции методами многомерной оптимизации, рассмотренными выше, при заданных параметрах;

- выводы об эффективности методов.

Требования к отчету:

В отчете должны быть представлены результаты выполнения указанных этапов и выводы к ним. Отчет представляется индивидуально каждым студентом.

Таблица 3.1

Варианты заданий

№	Вид функции f(X)	Начальная точка Х(1)	Точность
х1(1)	х2(1)
	(x1+2x2)2+(x2-3)2			0,01
	(x1-4x2)2+(x2+5)2		-5	0,01
	(x1-2x2)2+(x2+5)2	-15		0,02
	(x1+x2)2+(x2+4)2			0,01
	(x1-3x2)2+(x2-2)2			0,015
	(x1-3x2)2+(x2+1)2			0,01
	(x1+5x2)2+(x2-1)2			0,005
	(x1-2x2)2+(x2-3)2	-7	-7	0,01
	(x1+x2)2+(x2+2)2		-1	0,02
	(x1+x2)2+(x2+6)2			0,01
	(x1+x2)2+(x2-1)2			0,01
	(x1-2x2)2+(x2-3)2			0,02
	(x1+2x2)2+(x2-4)2	-4		0,02
	(x1-6x2)2+(x2+1)2	-5	-3	0,015
	(x1-5x2)2+(x2+6)2	-10	-5	0,015
	(x1+4x2)2+(x2-3)2	-5		0,01
	(x1+6x2)2+(x2+2)2	-10		0,01
	(x1-7x2)2+(x2-2)2			0,02
	(x1+3x2)2+(x2+5)2			0,02
	(x1-8x2)2+(x2+1)2	-5	-5	0,015
	(x1-x2)2+(x2-7)2			0,01
	(x1+8x2)2+(x2-2)2	-10		0,015
	(x1-5x2)2+(x2+3)2	-10	-5	0,01
	(x1-2x2)2+(x2-9)2			0,01
	(x1-6x2)2+(x2+9)2	-6	-5	0,01
	(x1+9x2)2+(x2-1)2			0,015
	(x1-3x2)2+(x2+5)2	-10		0,01
	(x1-4x2)2+(x2 -1)2			0,015
	(x1+4x2)2+(x2+1)2			0,01
	(x1-5x2)2+(x2+5)2			0,01

СПИСОК ЛИТЕРАТУРЫ

1. Мочалов С.П. Методы оптимизации металлургических процессов: Учебное пособие / КузПИ. –Кемерово, 1989.- 81с.

2. Поляк Б. Т. Введение в оптимизацию. -М.: Наука, 1983.

3. Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М. Методы оптимизации. -М.: Наука, 1975.

4. Банди. Методы оптимизации. -М.: Радио и связь, 1988.

5. Курицкий Б.Я. Поиск оптимальных решений средствами Ecxel 7.0. –СПб.: BHV – Санкт-Петербург, 1997.- 384с., ил.

Сергей Павлович Мочалов

Инна Анатольевна Рыбенко