Пример расчета экстремума функции методом сканирования

Постановка задачи. Определить экстремум функции f(x)=(x-2)²+7.

Определение экстремума аналитически. Необходимым условием существования экстремума является равенство нулю первой производной. Решаем уравнение f'(x)=2(x-2)=0. Полученная точка х*=2 является точкой минимума, так как вторая производная в данной точке f''(x*) =2>0.

Реализация метода сканирования. Выбираем достаточно большой начальный интервал [-100, 100] и количество разбиений n=10. Результаты расчетов точек и значений функции представлены в таблице 2.1.

Таблица 2.1

Результаты расчетов методом сканирования.

№	х	f(x)
	-100
	-80
	-60
	-40
	-20

Графический анализ функции Строим график функции на данном интервале (рис.2.1).

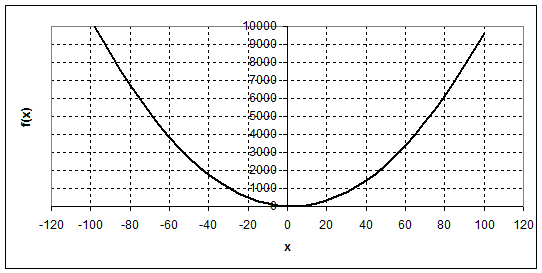
Рис.2.1

В результате реализации метода сканирования получена минимальная точка х*=0, значение функции в которой составляет f(x)=11. Границами интервала являются две точки по обе стороны от минимальной. Исходя из этого, делаем вывод, что экстремум находится в интервале
[a₁b₁]=[-20,20]. Этот интервал можно использовать в качестве начального при реализации других методов одномерной оптимизации либо двойного сканирования.

2.1.2. Метод локализации оптимума.

С целью повышения точности и уменьшения числа расчетов целевой функции используется процедура двойного сканирования. В начале необходимо определить [ 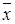- d, + d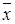], а затем вновь повторить сканирование. Этапы повторяются до достижения заданной точности. Этот метод называется локализацией оптимума. Он работает наиболее эффективно, если текущий интервал неопределенности делится на четыре части. При этом на начальном интервале вычисляются три точки на расстоянии (b₁-a₁)/4 друг от друга, затем рассчитывается значение функции в этих трех точках. Из полученных точек выбирается точка с минимальным значением функции и две точки по обе стороны от нее. Таким образом, получается новый интервал, для которого известны границы и середина интервала. После чего следует рассчитать только две новые точки по обе стороны от середины интервала. Расчет осуществляется до тех пор, пока длина конечного интервала не станет меньше заданной точности.

Алгоритм метода локализации оптимума.

Начальный этап. Выбрать начальный интервал [a₁, b₁] и точность поиска l. Задать k = 1, i=1 и перейти к основному этапу.

Основной этап. Шаг 1. Определить d_k=(b_k–a_k)/4. Вычислить значение х_ik=a_k + id_k и f(x_ik). Если i=3, то перейти к шагу 2, иначе положить i=i+1 и вернуться к шагу 1.

Шаг 2. Выбрать минимальное значение функции f(x_i) и соответствующее ему значение x_ik. Если i(min)=1, то a_к+1= a_к, b_к+1=x_2,k, x_{2, k+1}= x_{1, k..} Если i(min)=2, то a_к+1= x_{1, k}, b_к+1=x_3,k, x_{2, k+1}= x_{2, k..} Если i(min)=3, то a_к+1= x₂,_к, b_к+1=b_,k, x_2,k+1=x_3,k, положить k=k+1 и перейти к шагу 3.

Шаг 3. Если (b_k – a_k)<l, то остановиться, минимум функции находится на интервале [b_k – a_k]. Иначе, перейти к шагу 4.

Шаг 4. Вычислить d_k=(b_k – a_k)/4, x_1,k=a_k+d_k и x_3,k=a_k+3d_k , а также f(x_1,k ), f(x_3,k ). Перейти к шагу 2.

Пример расчета экстремума функции методом локализации оптимума.

Постановка задачи. Определить экстремум функции f(x)=(x-2)²+7 на полученном с использованием метода сканирования начальном интервале
[-20;20] с точностью l=0,5.

Расчет экстремума методом локализации оптимума для заданной задачи реализован средствами ECXEL. Результаты расчета представлены в таблице 2.2.

Таблица 2.2

Расчет экстремума функции f(x)=(x-2)²+7 методом локализации оптимума.

№	а	b	x1	x2	x3	f(x1)	f(x2)	f(x3)	|b-a|	Критерий
	-20.00	20.00	-10.00	0.00	10.00	151.00	11.00	71.00	40.00	не достигнут
	-10.00	10.00	-5.00	0.00	5.00	56.00	11.00	16.00	20.00	не достигнут
	-5.00	5.00	-2.50	0.00	2.50	27.25	11.00	7.25	10.00	не достигнут
	0.00	5.00	1.25	2.50	3.75	7.56	7.25	10.06	5.00	не достигнут
	1.25	3.75	1.88	2.50	3.13	7.02	7.25	8.27	2.50	не достигнут
	1.25	2.50	1.56	1.88	2.19	7.19	7.02	7.04	1.25	не достигнут
	1.56	2.19	1.72	1.88	2.03	7.08	7.02	7.00	0.63	не достигнут
	1.88	2.19	1.95	2.03	2.11	7.00	7.00	7.01	0.31	достигнут

После семи итераций и восьми расчетов значений функции интервал неопределенности составил [1,88; 2,19]. При этом |b₈ – a₈|=0,31, что меньше заданной величины 0,5. В качестве точки минимума может быть взята середина интервала 2,03. Следует отметить, что искомый минимум находится в точке х*=2.0.

2.1.3. Метод половинного деления.

Метод половинного деления является процедурой последовательного поиска. Используется стратегия выбора точек x₁ и y₁ на интервале [a₁, b₁], направленная на минимизацию максимумов из x₁ - a₁ и b₁ - y₁. Это может быть достигнуто расчетом точек x₁ и y₁, симметрично расположенных на расстоянии e>0 от середины интервала каждая. Здесь число e>0 настолько мало, чтобы длина нового интервала e + (b₁ - a₁)/2 являлась достаточно близкой к значению (b₁ - a₁)/2 и в то же время, чтобы значения функций f(x₁), f(y₁) были различны.

Алгоритм метода половинного деления.

Начальный этап. Выбрать константу 2e > 0, допустимую конечную длину интервала l > 0, начальный интервал [a₁, b₁]. Задать k = 1 и перейти к основному этапу.

Основной этап. Шаг 1. Если b_k - a_k < l то остановиться; точка минимума принадлежит интервалу [a_k, b_k], иначе вычислить

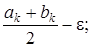x_k = y_k =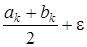

и перейти к шагу 2.

Шаг 2. Если f(x_k) < f(y_k) то a_k+1 = a_k и b_k+1 = y_k. В противном случае положить a_k+1 = x_k и b_k+1 = b_k . Заменить k = k + 1 и перейти к шагу 1.

Пример расчета экстремума функции методом половинного деления.

Постановка задачи. Определить экстремум функции f(x)=x₂-3x+2 на интервале
[-10;10] с точностью l=0,03 и константой различимости e=0,005 .

Результаты расчета с применением табличного процессора ECXEL по алгоритму, рассмотренному выше, представлены в таблице 2.3.

Таблица 2.3

Расчет экстремума функции f(x)=x₂-3x+2 методом половинного деления.

№	аk	bk	xk	yk	f(xk)	f(yk)	|b-a|	Критерий
	-10.000	10.000	-0.005	0.005	2.015	1.985	20.000	не достигнут
	-0.005	10.000	4.993	5.003	11.948	12.018	10.005	не достигнут
	-0.005	5.003	2.494	2.504	0.738	0.758	5.008	не достигнут
	-0.005	2.504	1.244	1.254	-0.185	-0.190	2.509	не достигнут
	1.244	2.504	1.869	1.879	-0.114	-0.106	1.259	не достигнут
	1.244	1.879	1.557	1.567	-0.247	-0.246	0.635	не достигнут
	1.244	1.567	1.401	1.411	-0.240	-0.242	0.322	не достигнут
	1.401	1.567	1.479	1.489	-0.250	-0.250	0.166	не достигнут
	1.479	1.567	1.518	1.528	-0.250	-0.249	0.088	не достигнут
	1.479	1.528	1.498	1.508	-0.250	-0.250	0.049	не достигнут
	1.479	1.508	1.488	1.498	-0.250	-0.250	0.030	достигнут

Таким образом, при поиске экстремума функции f(x)=x₂-3x+2 методом половинного деления после десяти итераций и одиннадцати вычислений значений функции интервал неопределенности составил [1,479; 1,508]. При этом |b₁₁ – a₁₁|=0,030, что равно заданной величине l=0,3. Следует отметить, что искомый минимум находится в точке х*=1,5.

2.1.4. Метод золотого сечения.

Представляет дальнейшее развитие метода половинного деления, когда при выполнении каждой итерации осуществляется только один раз расчет значения целевой функции.

Основные соотношения метода вытекают из следующих предпосылок. Пусть на k-ой итерации метода золотого сечения интервал неопределенности равен [a_k, b_k]. Точки x_k, y_k выбираются на основе следующих условий.

x_k=a_k+(1-a)×(b_k-a_k)

y_k=a_k+a×(b_k-a_k), где aÎ (0, 1)– коэффициент сжатия.

Длина нового интервала неопределенности определяется следующим способом: b_k+1 - a_k+1 = a(b_k - a_k)

Кроме того, должны выполняться равенства

b_k - x_k = y_k - a_k; x_k = a_k + (1 - a)(b_k - a_k); y_k = a_k +a(b_k - a_k).

Для новой итерации x_k+1 и y_k+1 выбираются так, что x_k+1 совпадает с y_k, или y_k+1 совпадает с x_k. Это условие обеспечивает возможность того, что на (k +1)-й итерации потребуется только одно новое вычисление функции.

При сравнении значений функции в двух точках возможны два варианта.
1. Если f(x_k) > f(y_k), то в этом случае a_k+1 = x_k и b_k+1 = b_k. При x_k+1 = y_k имеем y_k+1 = a_k+1 + a(b_k+1 - a_k+1) = x_k + a(b_k+1 - a_k+1). Подставляя в это выражение для x_k и y_k уравнения из предыдущего первого условия, получим, что a² + a - 1 = 0.

2. Если f(x_k) £ f(y_k), то в этом случае a_k+1 = a_k и b_k+1 = y_k. При y_k+1 = x_k имеем x_k+1 = a_k+1 + (1 - a)(b_k+1 - a_k+1) = a_k + (1 - a)(y_k - a_k). Подставляем в это выражение для x_k и y_k уравнения из предыдущего первого условия также получим a² + a - 1 = 0.

Корнями уравнения a² + a- 1=0 являются a= 0.618 и a= -1.618. Так как a должно быть из интервала (0, 1), то принимаем a= 0.618. На первой итерации метода необходимы два вычисления функции в точках x₁ и y₁, но на каждой последующей требуется только одно вычисление, так как либо x_k+1 = y_k, либо y_k+1 = x_k.

Алгоритм метода золотого сечения.

Начальный этап. Задается конечная длина интервала неопределенности l > 0, начальный интервал [a₁, b₁]. Вычислить x₁ = a₁ + (1 - a)(b₁ - a₁) и y₁ = a₁ + a(b₁ - a₁), приняв a = 0.618. Найти f(x₁), и f(y₁). Задать k = 1 и перейти к основному этапу.

Основной этап. Шаг 1. Если b_k - a_k < 1, то остановиться; оптимальная точка принадлежит интервалу [a_k, b_k]. При f(x_k) > f(y_k), перейти к шагу 2, если f(x_k) £ f(y_k), то к шагу 3.

Шаг 2. Положить a_k+1 = x_k; b_k+1 = b_k; x_k+1 = y_k; f(x_k+1) = f(y_k). Вычислить y_k+1 = a_k+1 + a(b_k+1 - a_k+1).

Вычислить f(y_k+1) и перейти к шагу 4.

Шаг 3. Положить а_k+1 = a_k, b_k+1 = y_k, y_k+1 = x_k, f(y_k+1) = f(x_k). Вычислить x_k+1 = a_k+1 + (1-a)(b_k+1 - a_k+1). Вычислить f(x_k+1) и перейти к шагу 4.

Шаг 4. Заменить k = k + 1 и перейти к шагу 1.

Пример расчета экстремума функции методом золотого сечения.

Постановка задачи. Минимизировать f(x) = x² + 2x на интервале xÎ[-3; 5] сократив его до величины l £ 0,2.

Рассчитываем минимум функции f(x) = x² + 2x с использованием табличного процессора ECXEL по рассмотренному выше алгоритму. Результаты расчетов представлены в таблице 2.4.

Таблица 2.4

Расчет экстремума функции f(x)= x² + 2x методом золотого сечения.

№	аk	bk	xk	yk	f(xk)	f(yk)	|b-a|	Критерий
	-3.000	5.000	0.056	1.944	0.115	7.667	8.000	не достигнут
	-3.000	1.944	-1.111	0.056	-0.988	0.116	4.944	не достигнут
	-3.000	0.056	-1.832	-1.111	-0.307	-0.988	3.056	не достигнут
	-1.832	0.056	-1.111	-0.665	-0.988	-0.888	1.889	не достигнут
	-1.832	-0.665	-1.387	-1.111	-0.851	-0.988	1.167	не достигнут
	-1.387	-0.665	-1.111	-0.941	-0.988	-0.996	0.721	не достигнут
	-1.111	-0.665	-0.941	-0.835	-0.996	-0.973	0.446	не достигнут
	-1.111	-0.835	-1.006	-0.941	-1.000	-0.996	0.276	не достигнут
	-1.111	-0.941	-1.046	-1.006	-0.998	-1.000	0.170	достигнут

После восьми итераций интервал неопределенности составил
[-1,111; -0,941]. При этом |b₉ - a₉|=0,170, что меньше заданной величины 0,2. В качестве точки минимума может быть взята середина интервала -1,026. Искомый минимум равен ‑1,0.

2.1.5. Метод Фибоначчи.

В отличие от рассмотренных поисковых процедур в методе Фибоначчи используется числовая последовательность, поэтому общее число n вычислений функции заранее задается. Это объясняется тем, что точки, в которых производятся вычисления, определяются по зависящим от n формулам

x_k = a_k + 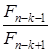(b_k - a_k), k = 1, …, n - 1;

y_k = a_k + 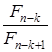(b_k - a_k), k = 1, …, n - 1.

где F_j =F_j-1 + F_j-2, j = 3, 4, …; F₀=F₁=1 называется последовательностью чисел Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,...). В этом методе длина интервала неопределенности на k-й итерации сократится от b₁ - a₁ до (b₁ - a₁)/F_n. Поэтому для требуемой точности можно заранее рассчитать величину F_n и количество вычислений функции.

Алгоритм метода Фибоначчи.

Начальный этап. Задается конечная длина интервала l > 0 и константа различимости e > 0, начальный интервал [a₁, b₁]. Выбрать число вычислений функции n так, чтобы F_n > (b₁ - a₁)/l. Вычислить x₁ = a₁ + (F_n-2/F_n)(b₁ - a₁), y₁ = a₁+(F_n-1/F_n)(b₁-a₁); f(x₁); f(y₁) . Принять k = 1 и перейти к основному этапу.

Основной этап. Шаг 1. Если f(x_k) > f(y_k), то перейти к шагу 2, если f(x_k) £ f(y_k), то к шагу 3.

Шаг 2. Принять a_k+1 = x_k; b_k+1 = b_k. Затем вычислить x_k+1 = y_k, y_k+1 = a_k+1 + (F_n-k-1/F_n-k)×(b_k+1 - a_k+1). Если k = n - 2, то перейти к шагу 4.

Шаг 3. Принять a_k+1 = a_k; b_k+1 = y_k; x_k+1 =a_k+1 + (F_n-k-2/F_n-k)×(b_k+1 - a_k+1). Если k = n - 2, то перейти к шагу 5, иначе вычислить f(x_k+1) и перейти к шагу 4.

Шаг 4. Присвоить k = k + 1 и перейти к шагу 1.

Шаг 5. Принять x_n = x_n-1 и y_n = x_n+e . Если f(x_n) > f(y_n) , то a_n = x_n и b_n = b_n‑1. При f(x_n) £ f(y_n) вычислить a_n = a_n-1 и b_n = у_n и остановиться.

Оптимальное решение содержится в интервале [a_n, b_n].