Пример расчета минимума функции методом деформируемого многогранника
Постановка задачи. Рассматриваем задачу минимизации функции
f(X)=(x1-2)4+ (х1 - 2х2)2.
Вершины начального многогранника рассчитываем как в обычном симплексе
X1(1) = [2.25 2.36]Т; X2(1) = [2.5 2.78]Т; X3(1) = [2.75 2.36]Т.
Зададим параметры алгоритма a = 1; b = 0,5; g = 2.
На первой итерации при k = 1. Вычислим значение функции в вершинах исходного многогранника
f(X1(1)) = 6.10480; f(X2(1)) = 9.4261; f(X3(1)) = 4.197.
Наихудшей вершиной является Xh(1) = X2(1), а наилучшей Xl(1) = X3(1).
Определяем центр тяжести
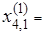 [(2.25+ 2.50 + 2.75) – 2.5]/2 = 2.5,
[(2.25+ 2.50 + 2.75) – 2.5]/2 = 2.5,
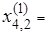 [(2.36 + 2.78 + 2.36) – 2.78]/2 = 2.36.
[(2.36 + 2.78 + 2.36) – 2.78]/2 = 2.36.
и рассчитываем координату отражения
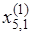 = 2.5 + 1(2.5 – 2.5) = 2.5,
= 2.5 + 1(2.5 – 2.5) = 2.5,
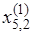 = 2.5 + 1(2.5 – 2.78) = 1.94.
= 2.5 + 1(2.5 – 2.78) = 1.94.
Значение функции в этой точке f(X5(1)) = 1.967, что меньше, чем в X1(1). Поэтому, проводим операцию растяжения
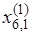 = 2.5 + 2(2.5 – 2.5) = 2,5,
= 2.5 + 2(2.5 – 2.5) = 2,5,
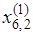 = 2.5 + 2(2.22 – 2.5) = 1.52.
= 2.5 + 2(2.22 – 2.5) = 1.52.
Значение функции f(2.5 1.52) = 0.354. Поскольку f(X6(1)) < f(X5(1)), заменяем X2(1) на X6(1) и полагаем X6(1) = X1(2) на следующем этапе поиска. Результаты расчета нескольких итераций метода представлены в таблице 2.5. Траектория поиска метода представлена на рис.2.5.
Таблица 2.5
Результаты расчета минимума функции f(X) = (x1 - 2)4 + (х1 - 2х2)2.
методом Нелдера-Мида.
| № | Операция | x1 | x2 | f(X) | № | Операция | x1 | x2 | f(X) | № | Операция | x1 | x2 | f(X) |
| вершина 1 | 2.25 | 2.36 | 6.105 | вершина 1 | 2.81 | 1.73 | 0.855 | вершина 1 | 2.30 | 1.05 | 0.049 | |||
| вершина 2 | 2.50 | 2.78 | 9.426 | вершина 2 | 2.75 | 2.36 | 4.197 | вершина 2 | 2.50 | 1.52 | 0.354 | |||
| вершина 3 | 2.75 | 2.36 | 4.197 | вершина 3 | 2.50 | 1.52 | 0.354 | вершина 3 | 2.61 | 1.26 | 0.147 | |||
| ц. тяжести | 2.50 | 2.36 | 4.991 | ц. тяжести | 2.66 | 1.63 | 0.538 | ц. тяжести | 2.45 | 1.15 | 0.064 | |||
| отражение | 2.50 | 1.94 | 1.967 | отражение | 2.56 | 0.89 | 0.712 | отражение | 2.41 | 0.79 | 0.727 | |||
| растяжение | 2.50 | 1.52 | 0.354 | сжатие | 2.61 | 1.26 | 0.147 | редукция | ||||||
| вершина 1 | 2.25 | 2.36 | 6.105 | вершина 1 | 2.81 | 1.73 | 0.855 | |||||||
| вершина 2 | 2.75 | 2.36 | 4.197 | вершина 2 | 2.50 | 1.52 | 0.354 | |||||||
| вершина 3 | 2.50 | 1.52 | 0.354 | вершина 3 | 2.61 | 1.26 | 0.147 | |||||||
| ц. тяжести | 2.63 | 1.94 | 1.728 | ц. тяжести | 2.55 | 1.39 | 0.144 | |||||||
| отражение | 3.00 | 1.52 | 1.002 | отражение | 2.30 | 1.05 | 0.049 | |||||||
| сжатие | 2.81 | 1.73 | 0.855 | растяжение | 2.04 | 0.71 | 0.393 |



















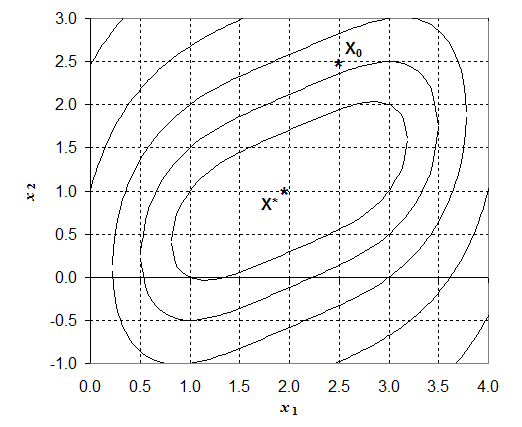 |
На пятой итерации симплекс достиг области экстремума, что говорит о высокой эффективности метода. Отраженная вершина вновь становится «наихудшей», поэтому для достижения необходимой точности необходимо провести редукцию.
Рис.2.5 Графическая иллюстрация поиска минимума функции методом Нелдера-Мида.
Методы с использованием производных 1-го порядка
Градиентный метод
Стратегия обычного градиентного метода оптимизации без ограничений использует только первые производные целевой функции. На k-м этапе переход из точки Х(k) в точку Х(k+1) описывается следующим соотношением:
X(k+1) = X(k) + DX(k) = X(k) + l(k)× 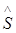 (k),
(k),
где DX(k) - вектор перехода из точки Х(k) в точку Х(k+1);
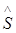 (k) - единичный вектор в направлении DX(k);
(k) - единичный вектор в направлении DX(k);
l(k) - скаляр, равный величине шага.
Величина шага l(k) в процессе движения остается постоянной. В ряде случаев предусматривается адаптация к топологии поверхности. Градиент целевой функции f(Х) в любой точке Х есть вектор в направлении наибольшего локального увеличения f(Х). Следовательно, нужно двигаться в направлении, противоположном градиенту f(Х), поскольку отрицательный градиент f(Х) в точке Х(k) направлен в сторону наибольшего уменьшения f(Х) по всем компонентам Х и ортогонален линии уровня f(Х) в точке Х(k). Введение направления, противоположного нормированному (единичному) градиенту f(Х), определяемого в точке Х(k) определяется по формуле
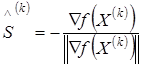 ,
,
тогда
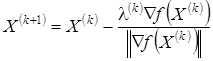 .
.
При расчете экстремума функции градиентным методом при переходе к минимуму или в овражных ситуациях возникает характерный случай, который заключается в зигзагообразном движении. Поэтому величину шага необходимо уменьшать. Одним из возможных подходов к адаптации является расчет угла j между последовательными векторами шагов. При малых j величину шага следует уменьшать, а при больших соответственно увеличивать. Это позволяет сократить число шагов и повышает работоспособность метода.
