Приближенные вычисления

При решении задач вычислительного характера, редко удается получить абсолютно точные результаты. Причинами этого являются участвующие в вычислениях операции деления. Если исходные числа были иррациональными, то точно представить их в виде конечных десятичных дробей невозможно, так как их запись содержит бесконечное число цифр. Поэтому, приходиться вместо исходных иррациональных чисел, оперировать рациональными числами, полученными из данных иррациональных чисел путем записи их в рациональном виде, путем записи их с конечным числом знаков, то есть округлении.

Возникают подобные ситуации, и в случае когда исходные числа были рациональными, а в результате операций над ними получились иррациональные, например при делении единицы на три получим 1/3=0,333…, в результате выполнения операций подобные числа так же округляются до конечного числа знаков.

Кроме того, одним из самых важных источников погрешности, является неточность самих исходных данных. Обычно исходные данные для большинства задач моделирования получают на основе физических экспериментов и опытов. Любой эксперимент связан с измерениями и наблюдениями, которые сами по себе не могут оказаться абсолютно точными в связи с возможностями измерительной аппаратуры. Даже при определении площади комнаты, когда необходимо знать только ее длину и ширину, как бы мы не старались, мы не сможем измерить абсолютно точно, даже сам измерительный прибор, заранее содержит какую то погрешность измерений. И естественно, при решении задач мы идеализируем их исходные данные, то есть вместо реальных задач решаем приближенную к реальности идеальную задачу, даже с измерением площади комнаты, углы не могут быть абсолютно прямыми, то есть комната заранее не является прямоугольником.

Пусть для величины, точное значение которой есть X, мы получили некоторое приближенное значение X^*. Абсолютная величина разности между точным значением X и его приближенное величиной X^*, называется абсолютной погрешностью. Приближенного числа X^*, и обозначается 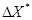, то есть, 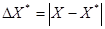. Как правило, точное значение X нам неизвестно, как неизвестна и абсолютная погрешность 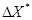. Но зато, можно определить число, которое эта погрешность заведомо не превосходит. Его обычно и принимают за абсолютное значение погрешности искомой величины. Так при взвешивании какого либо предмета на аптекарских весах, мы не можем определить точный вес предмета, однако гарантируем, что погрешность взвешивания не будет превышать 0,01 г. Эту величину и называют абсолютной погрешностью.

Абсолютная погрешность далеко не всегда точно характеризует погрешность вычислений. Так например, пусть погрешность взвешивания предмета равна 100 г, если взвешивался например автомобиль, то эта погрешность очень мала, а если взвешивался например телефон, то эта погрешность очень велика. Поэтому было введено еще одно важное, с точки зрения точности вычислений понятие – это относительная погрешность.

Относительной погрешностью приближенного значения X^* называют отношение абсолютной погрешности 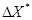к абсолютному значению величины.

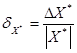
Для примера возьмем измерения длин радиоволн с абсолютной погрешностью равной одному метру. Если после измерений получим, что длина волны равна 1000 метров, то относительная погрешность равна 1/1000=0,001, а если длина волны равна 4 метрам, то относительная погрешность равна 1/4=0,25.

Для удобства анализа относительной погрешности очень часто ее представляют в виде процентов к значению измерений:

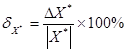
тогда, в результате решения задачи измерения длины волны, в случае если это километровый диапазон, то относительная погрешность составляет всего 0,1%, то есть очень мало, а если метровый, то 25%, то есть очень много.

Как говорилось ранее, очень часто в процессе вычислений приходиться иметь дело с бесконечными дробями. Такие числа приходиться округлять. Обычно округление производят по следующему правилу (иногда бывает необходимость использования и других правил). Пусть какое то число имеет в своей записи более чем k цифровых знаков и мы хотим округлить его, оставив ровно k знаков. Тогда, если (k+1)-я цифра числа меньше чем 5, то все ее цифры, начиная с (k+1)-ой просто отбрасываются, а если (k+1)-я цифра больше чем 5, то все цифры, начиная с (k+1)-ой тоже отбрасываются, при этом k-я цифра увеличивается на единицу. Если (k+1)-я цифра есть 5, а за ней найдется хоть одна отличная от нуля цифра, то поступают, как в случае, если (k+1)-я цифра больше пяти, если за ней нет цифр отличных от нуля, тогда отбрасывают «хвост», начиная с (k+1)-ой цифры, и если k-я цифра четная, то оставляют ее без изменений, если нечетная, увеличивают на единицу. Например, оставив три знака после запятой в числе 5,6785 поучим 5,678, а если оставим три знака после запятой в числе 4,5675, то получим 4,568.

Принято считать, что в приближенном значении величины все цифры верные, если его абсолютная погрешность не превосходит единицы последнего разряда. При выполнении этого условия можно по записи приближенного значения определить его абсолютную погрешность. И наоборот, по абсолютной погрешности числа, можно определить число верных знаков в его записи. Например, если известно, что все цифры записи числа X=15 верны, то его абсолютная погрешность 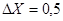, а если известно, что все цифры записи числа X=3,14 верны, то его абсолютная погрешность 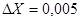. Аналогично наоборот, если задано число X=1,2345 и абсолютная погрешность при этом 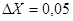, то можно говорить о том, что верны только цифры 1 и 2, то есть можно считать верным только число X=1,2 и в окончательном результате остальные цифры должны отбрасываться.

В процессе алгоритмизации, то есть разработки алгоритмов решения различных задач следует обратить должное внимание на качество вычислительных и измерительных операций и анализу погрешности результатов.