Упорядоченное множество
Содержание
1. Математика. Логические основы персональных компьютеров (ПК).. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 -28
· Множества, графы, системы счисления. (А,В). . . . . . . . . . . 2- 16
· Комбинаторика и теория вероятностей. (Г) . . . . . . . . . . . . .16- 22
· Элементы математической логики. (Е) . . . . . . . . . . . . . . . . 22-28
2. Информатика.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28- 67
· Компьютер как техническая база современных информационных технологий. (И) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28- 33
· Программное обеспечение (ПО) персонального компьютера. (Системы ПО). (Р,С) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33- 48
· Прикладное программное обеспечение ПК. (Текстовые редакторы, Табличные процессоры - электронные таблицы). (Т,Ш) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48- 61
· Средства разработки программ для ПК. (Я) . . . . . . . . . . . . 62-67
Список использованной литературы. . . . . . . . . . . . . . . . . . . . . . . . . . 68- 69
Математика. Логические основы персональных компьютеров (ПК).
· Множества, графы, системы счисления. (А)
Понятие множества. Виды множества. Действия над множествами. Свойства действий над множествами. Графы. Элементы графов. Представление графов в ЭВМ.
Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Основное отношение между элементом a и содержащим его множеством A обозначается так 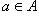 (a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут
(a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут 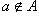 (a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так {a, b, c} обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем не выписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3, ...}, а множество четных чисел {2, 4, 6, ...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.
(a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так {a, b, c} обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем не выписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3, ...}, а множество четных чисел {2, 4, 6, ...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.
Объекты, составляющие множество, называются элементами множества.
Вот что сказано о множестве у самого Кантора:
Под множеством мы понимаем любое объединение в единое целое M определенных вполне различаемых объектов m из нашего восприятия или мысли.
Пример:
Множество действительных чисел, множество натуральных чисел, множество жителей данного города, множество деревьев на земле.
Среди множеств выделяют особое множество - пустое множество.
Пустое множество
-множество, не содержащее ни одного элемента.
Пустое множество является частью любого множества.
Пример:
Множество всех действительных корней уравнения 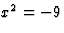 пусто.
пусто.
Множество считается определенным , если указаны все его элементы. Эти элементы могут быть указаны с помощью некоторого общего признака или с помощью некоторого списка, где обозначены все элементы. Последний способ возможен только в том случае, если множество имеет конечное число элементов.
Конечное множество
-множество, состоящее из конечного числа элементов.
Комбинаторика есть теория конечных множеств. Поэтому далее будем иметь дело лишь с конечными множествами.
Пример:
Множество всех студентов факультета математики и информатики.
Основной характеристикой конечного множества является число его элементов.
Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из первых с помощью некоторых операций.
Бесконечное множество
-непустое множество, не являющееся конечным.
Пример:
Множество натуральных чисел является бесконечным.
Упорядоченное множество
Множество, каждому элементу которого поставлено в соответствие некоторое число (немер этого элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.
Каждое конечное множество можно сделать упорядоченным, если, например, переписать все элементы в некоторый список (a, b, c, d,...), а затем поставить в соответствие каждому элементу номер места, нк котором он стоит в списке.
