Цифровой сигнал и дискретная модуляция

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ. 1

ЗАДАНИЕ. 2

ЦИФРОВАЯ СИСТЕМА СВЯЗИ И АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ. 3

ЦИФРОВОЙ СИГНАЛ И ДИСКРЕТНАЯ МОДУЛЯЦИЯ. 5

ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНОГО СИГНАЛА ПО ДИСКРЕТНЫМ ОТСЧЕТАМ... 8

АНАЛОГОВАЯ СИСТЕМА СВЯЗИ И ЛИНЕЙНЫЕ ВИДЫ МОДУЛЯЦИИ.. 11

ДЕТЕКТИРОВАНИЕ СИГНАЛОВ С ЛИНЕЙНЫМИ ВИДАМИ МОДУЛЯЦИИ.. 15

УГЛОВАЯ (ЧМ И ФМ) МОДУЛЯЦИЯ. 16

ЛИТЕРАТУРА.. 20

ЗАДАНИЕ

Данная курсовая работа охватывает следующие разделы программы: общие сведения о системах электросвязи, математические модели сообщений и сигналов, методы формирования и преобразования сигналов.

Необходимо выполнить задание по разделам: цифровая система связи и аналого-цифровой преобразователь, восстановление непрерывного сигнала по дискретным отсчетам, детектирование сигналов с линейными видами модуляции, угловая (ЧМ и ФМ) модуляция.

ИСХОДНЫЕ ДАННЫЕ

Верхняя частота спектра аналогового сигнала F_В = 4 кГц.

Число уровней квантования L = 256.

Номер уровня j = 248.

Вид дискретной модуляции – ОФМ.

Коэффициент пропорциональности k = 1.35

Амплитуда модулирующего сигнала A = 2 В.

Частота F = 2.5 кГц.

Ф = 180 град.

Амплитуда U_н = 6 В.

Сигнал ОМ, детектор – синхронный.

K = 2.5 рад/В, A = 1.6 В, F = 3 кГц, n=2 F↓.

ЦИФРОВАЯ СИСТЕМА СВЯЗИ И АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ

Требуется:

1. Изобразить обобщенную структурную схему цифровой системы связи.

2. Кратко пояснить назначение всех элементов системы связи.

3. Изобразить аналого-цифровой преобразователь (АЦП), т.е. структурную схему устройства для преобразования непрерывного сигнала в дискретно-двоичный (цифровой) сигнал.

4. Нарисовать временные диаграммы, иллюстрирующие указанный процесс преобразования.

5. Рассчитать скорость передачи Vk двоичных символов на выходе АЦП при заданном числе уровней квантования L и верхней граничной частоте F_В источника непрерывных сообщений. Значения F_В и L по вариантам приведены в табл. П1.

Решение:

1. Структурная схема системы связи.

ИС

^/#

КОДЕР

МОДУЛЯТОР

ЛИНИЯ СВЯЗИ

ДЕМОДУЛЯТОР

ДЕКОДЕР

#/^

ФИЛЬТР

Рис. 1. Структурная схема цифровой системы связи

2. Назначение элементов системы связи.

Источник сообщения

Источник создает непрерывное сообщение Х(t) – случайный квазибелый стационарный эргодический процесс, мощность которого сосредоточена в области частот от 0 до Fв. Мгновенные значения процесса Х(t) равновероятны в интервале от а_min до а_max.

Аналого-цифровой преобразователь

Для передачи аналогового сигнала по цифровому каналу связи необходимо его преобразование в цифровой поток двоичных символов «0» и «1». Такое преобразование приводит к дискретизации процесса Х(t) с постоянным интервалом Δt (замене непрерывного сигнала x(t) последовательностью отсчетов его мгновенных значений в дискретные моменты времени x(t_i), i = 0, ±1, ±2, …) и квантованию – представлению полученных отсчетов в виде двоичных чисел, разрядность которых определяется заданной точностью.

Кодер

Кодер выполняет систематическое кодирование с одной проверкой на четность, образуя помехоустойчивый код (k+1,k). Поступающие на вхо кодека k-разрядные последовательности информационных символов преобразуются в (k+1)-разрядные кодовые комбинации, в которых к k информационным символам добавляются по одному проверочному символу. Сигнал B(t) на выходе кодера представляет собой случайный синхронный телеграфный сигнал.

Модулятор

В модуляторе случайный синхронный телеграфный сигнал производит модуляцию гармонического несущего колебания uн(t) = Ucos2πft в соответствии с видом модуляции.

Демодулятор

Демодулятор осуществляет когерентную обработку наблюдаемой реализации смеси сигнала и шума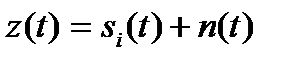

Декодер и ЦАП

Декодер канального кода (k+1,k) анализирует принимаемые кодовые комбинации длины k+1 и либо преобразует их в последовательности информационных символов длины k для последующего цифро-аналогового преобразования в уровень отсчета первичного сигнала , либо отказывается от последующего декодирования, выдавая сообщение об обнаружении ошибки.

Фильтр

Фильтр – восстановитель сглаживает сигнал ступенчатой формы, поступающий с выхода ЦАП, и тем самым обеспечивает восстановление формы передаваемого аналогового сигнала x(t) с минимально возможной погрешностью.

3. Схема АЦП.

АЦП, как правило, устанавливаются в цепях обратных связей цифровых систем управления для преобразования аналоговых сигналов обратных связей в коды, воспринимаемые цифровой частью системы. Т.о. АЦП выполняют несколько функций, таких как: временная дискретизация, квантование по уровню, кодирование.

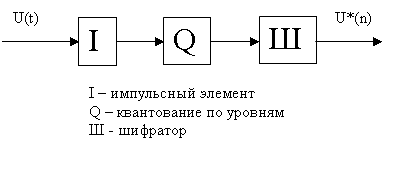
Рис. 2. Структурная схема АЦП

4. Временные диаграммы.

[Л1]

Так как в моем варианте число уровней квантования L = 256, то разрядность k двоичных чисел для цифрового выражения уровней квантования будет равна:

k = 8

5. Расчет скорости передачи Vk двоичных символов на выходе АЦП.

Найдем интервал дискретизации ∆t в соответствии с теоремой отсчетов, по формуле:

[Л1]

Разрядность k двоичных чисел для цифрового выражения уровней квантования была определена ранее и равна: k = 8

.Длительность Т каждого разряда кодовой комбинации

[Л1]

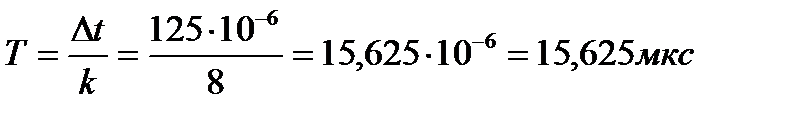
Таким образом, скорость передачи Vk двоичных символов на выходе АЦП равна:

[Л1]

ЦИФРОВОЙ СИГНАЛ И ДИСКРЕТНАЯ МОДУЛЯЦИЯ

На вход АЦП в течение длительного времени подается сигнал с постоянным уровнем, равным 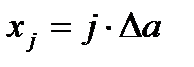(∆a=0.1В – шаг квантования по уровню, j – в соответствии с номером варианта берется из табл. П1).

Квантованные уровни на вход кодера АЦП следуют через промежутки времени ∆t. По высоте, очевидно, они одинаковы и равны 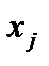каждый. На выходе примитивного кодера эта последовательность квантованных уровней кодируется одинаковыми кодовыми комбинациями. Таким образом, на выходе АЦП получается периодическая последовательность одинаковых кодовых комбинаций с периодом 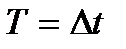. В каждом варианте кодовая комбинация соответствует записи номера уровня j в двоичной системе счисления.

Для всех вариантов следует принять, что передаче нулевых символов соответствует нулевой уровень, а передаче единичных +1В (униполярный сигнал). Длительность импульса принимается:

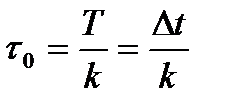
Требуется:

1.Записать k-разрядное двоичное число, соответствующее уровню квантования 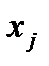. Величина определена ранее. В случае необходимости заполнить старшие разряды числа нулями.

2.Изобразить одну под другой три временные диаграммы.

2.1.Постоянный по уровню непрерывный сигнал на входе АЦП.

2.2.Квантованный по уровню и по времени сигнал.

2.3.Дискретный двоичный (цифровой) сигнал на выходе кодера АЦП, т.е. периодическую последовательность одинаковых кодовых комбинаций, передающих двоичным кодом номер j.

3.Найти выражение для спектральной функции S(jω) кодовой комбинации, занимающей время .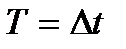

4.Найти спектр амплитуд цифрового периодического сигнала (п. 2.3) и изобразить этот спектр.

5.Установить (ограничить) ширину спектра ∆F цифрового сигнала (п. 2.3) 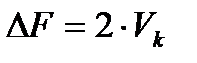. Сравнить верхнюю частоту непрерывного сигнала и ∆F.

6.Изобразить одну под другой временные диаграммы модулирующего u(t) (п. 2.3) и модулированного s(t) сигналов для вида модуляции, указанного в табл. П1. Для ОФМ изобразить также временную диаграмму перекодированного сигнала.

Решение:

1. Из рассчитанного ранее найдем k-разрядное двоичное число, исходя из уровня квантования .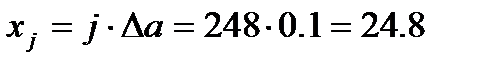

248₁₀ = 11111000₂

b(t)

Осциллограмма отклика АЦП на уровень с номером 248 имеет вид, представленный на рис.3.

1 1 1 1 1 0 0 0

1 2 3 4 5 6 7 8

Рис.3. Отклик АЦП на уровень с номером 248

Периодический сигнал u(t) можно записать в виде ряда Фурье:

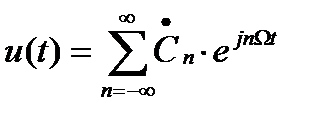, где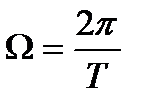

Определим спектральную функцию S(jw) для одной кодовой комбинации, занимающей период T = ∆t. Нахождение S(jw) сводится к нахождению спектральной функции для одиночного импульса длительностью 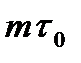, где m=5.

Рис. 4. Периодически повторяющаяся кодовая комбинация 11111000

Таким образом:

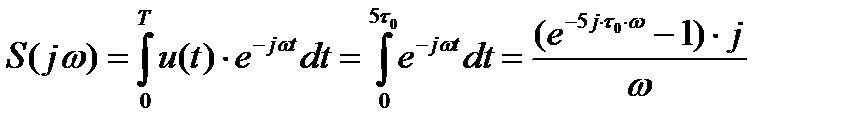
Далее найдем спектр амплитуд цифрового периодического сигнала, заменив частоту w на :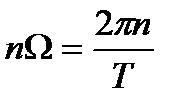

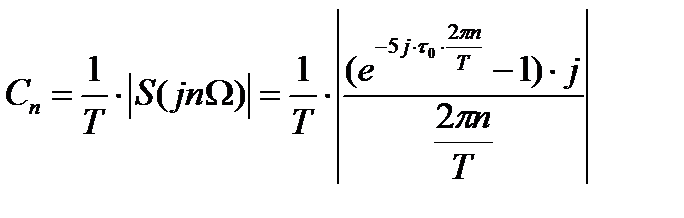
Теоретически ряд Фурье содержит бесконечное число составляющих. Ограничим его до n=16, тогда спектр амплитуд, рассчитанный в компьютерной среде Mathcad, будет иметь вид рис.5 (кривой линией показана огибающая спектра):

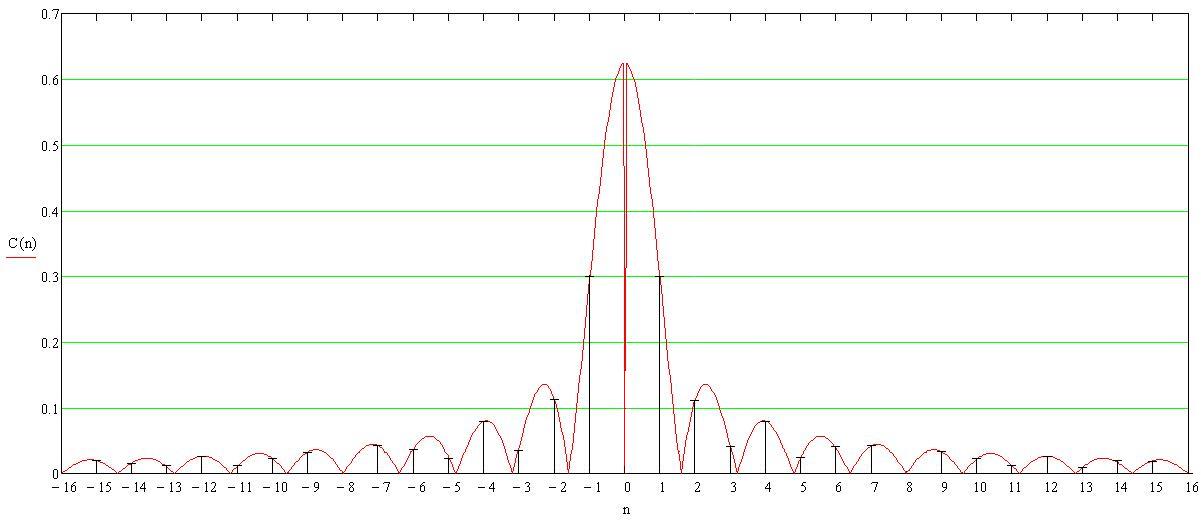
Рис.5 Спектр амплитуд периодически повторяющейся кодовой комбинации 11111000

Изобразим одну под другой временные диаграммы модулирующего u(t) и модулированного s(t) сигналов для ОФМ.

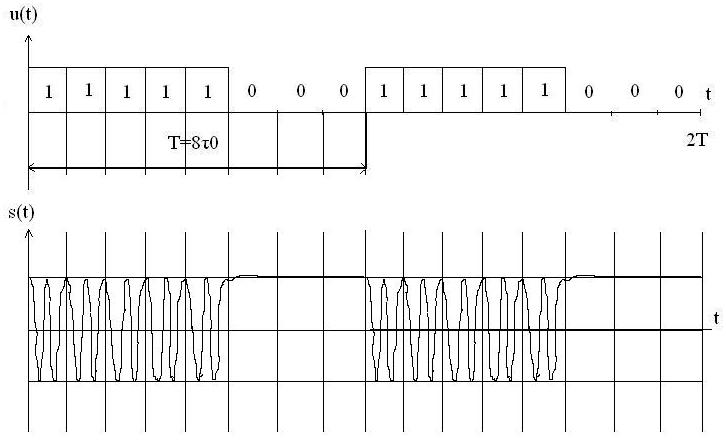
Рис.6 Временные диаграммы u(t) и s(t) для ОФМ