Алгебраические фракталы. Рис. 85. Фрактал Мандельброта
 |
Рис. 85. Фрактал Мандельброта
Вторая большая группа фракталов – алгебраические. Свое название они получили, за то, что их строят, используя простые алгебраические формулы.
Получают их с помощью нелинейных процессов в n-мерных пространствах. Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. Состояние, в котором окажется динамическая система после некоторого числа итераций, зависит от начальных условий. Поэтому каждое устойчивое состояние (аттрактор) обладает некоторой областью начальных состояний, при которых система обязательно перейдет в рассматриваемые конечные состояния. Таким образом, фазовое пространство разбивается на области притяжения аттракторов.
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона и т.д.
Фрактал Мандельброта назван по имени французского математика польского происхождения Бенуа Мандельброта, известного исследователя фракталов.
Множество Мандельброта получают следующим образом: строится отображение z'=fc(z), где числа z и c - комплексные.
Алгоритм построения множества Мандельброта выглядит следующим образом:
1. выбираем значение c
2. z:=0 n:=0
3. z:=f(z)
4. inc(n)
Если не достигнуто максимальное значение итераций или значение z не превысило максимального значения, то повторять шаги 3 и 4.
Наиболее часто используется формула z = z2 + c, так как она наиболее проста в применении. Раскладывая уравнение на действительную и мнимую часть, получаем следующее:
Re: x2- y2+ a
Im: 2xy + b,
приняв, что z = x + yi и c = a + bi.
Цвет обычно выбирают по числу итераций, но есть и другие способы.
Текст программы выглядит следующим образом.
Program M2;
Uses Graph, Crt;
Type
TComplex = Record
X : Real;
Y : Real;
End;
Const
iter = 50;
max = 16;
Var
z, t, c : TComplex;
x, y, n : Integer;
Cancel : Boolean;
gd, gm : Integer;
mx, my : Integer;
Begin
Cancel := False;
Randomize;
gd := Detect;
InitGraph(gd,gm,'e:\bp\bgi');
Mx := GetMaxX div 2;
My := GetMaxY div 2;
For y := -my to my do
For x := -mx to mx do Begin
n := 0;
C.X := X * 0.005;
C.Y := Y * 0.005;
z.X := 0;
z.Y := 0;
While (sqr(z.X) + sqr(z.Y) < max) and (n < iter) do Begin
t := z;
Z.X := sqr(t.X) - sqr(t.Y) + C.X;
Z.Y := 2 * t.X * t.Y+ C.Y;
Inc(n);
If keypressed then cancel := true;
End;
If n < iter then Begin
PutPixel(mx + x,my + y,16 - (n mod 16));
End;
If cancel then exit;
End;
Readkey;
CloseGraph;
end.
А теперь опишем программу словами. Для всех точек на комплексной плоскости в некотором интервале вычисляем достаточно большое количество раз z = z2 + c, каждый раз проверяя абсолютное значение z. Если это значение больше максимального, то рисуем точку с цветом, вычисляемым по количеству итераций, иначе рисуем точку черного цвета.
Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное - это границы множества. Они то и являются фрактальными. Если рассмотреть увеличение, то можно увидеть самоподобие фигуры.
Увеличение фракталов.
Для того чтобы увеличить данный объект, необходимо изменить коэффициенты в следующем куске кода:
C.X:=X*0.005;
C.Y:=Y*0.005;
Чем меньше число, тем больше увеличение и наоборот. Для того чтобы сместить множество, нужно прибавлять или вычитать числа в том же куске кода. Рассмотрим в общем случае:
C.X := X*m + dx;
C.Y := Y*m + dy;
 |
Здесь m задет увеличение, dx - смещение по горизонтали, а dy - смещение по вертикали. Например, положив, что m=0.0001, dx=-1.2, dy=-0.3, мы получим примерно то, что изображено на рисунке (рис. 86).
Рис. 86
 |
6.5. Стохастические фракталы
Рис. 87. Стохастический фрактал
Кривая Коха как бы не была похожа на границу берега не может выступать в качестве ее модели из-за того, что она всюду одинакова, самоподобна, а в действительности это не так. Все природные объекты создаются по капризу природы, и есть случайность в этом процессе.
Фракталы при построении которых в итеративной системе случайным образом изменяются какие-либо параметры называются стохастичными. Термин "стохастичность" происходит от греческого слова, обозначающего "предположение".
Также примером случайности в природе является броуновское движение. С помощью компьютера такие процессы строить достаточно просто, т.к. он позволяет генерировать последовательности случайных чисел. Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.
Построение ландшафта
Возьмем карту размером 512*512 точек, каждая из которых представляет собой 8-ми битное целое значение высоты и цвета. Первоначально изображение выглядит таким образом, что при вызове функции высоты в точках с координатами (u,v) она возвращает одинаковые значения в углах условной сетки точек. Т. е. w(0,0)=w(512,0)=w(0, 512)=w(512, 512). w(1,1)=w(512, 512) и т. д.
Координаты поверхности:
Координаты (u,v) описывают положение на поверхности. Всю поверхность можно представить как множество дискретных значений функции высоты h=w(u,v).
Координаты экрана:
Положение точек на экране будем описывать координатами (x,y).
Построение поверхности:
Генерация фрактальных поверхностей, по другому, называется плазма или рекурсивное разбиение и выглядит следующим образом. В начале вычисляем произвольные высоты в углах и середине карты поверхности т. е. в точках: (0,0), (512,0), (0, 512), (512, 512) (рис. 88 a,b). Затем запускаем подпрограмму вычисления высот, для которой в качестве параметров передаются размер и положение квадратного участка поверхности, в первом случае этим участком является вся карта. Подпрограмма считывает значения высот из углов квадрата полученного в качестве параметра. Вдоль каждого ребра квадрата вычисляется среднее значение двух высот по краям ребра и к полученному значению прибавляется некоторое произвольное значение, пропорциональное длине ребра, результат записывается в точку, делящую ребро пополам (рис. 88 c). Затем вычисляется высота центра квадрата путем нахождения средней высоты четырех высот углов квадрата, и к полученному значению добавляют произвольное число (рис. 88 d).
В 3-х мерном изображении этот процесс будет выглядеть следующим образом.
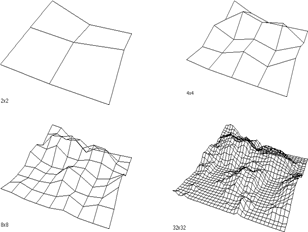 |
Рис. 88
Для получения более гладких поверхностей используют метод «смазывания», который предполагает пересчет вершин поверхности по следующей формуле:
w(u,v)=k1*w(u,v)+k2*w(u+3,v-2)+k3*w(u2,v+4).
Причем k1, k2, k3 подбирают таким образом чтобы k1+k2+k3=1.
Все вычисления производятся в фиксированных точках целочисленной арифметики.

Рис. 89. Примеры фрактальных ландшафтов
Приведем программу построения стохастического фрактала «Плазма».

Рис.90. Фрактал «Плазма»
Program Plazma;
Uses CRT, Graph;
Var
Plasma : Array [0..319, 0..199] of Byte;
x, y, j: Integer;
gd, gm : Integer;
Procedure RGB(N, R, G, B:Word);
Begin
Port[$3c8]:=n;
Port[$3c9]:=R div 4;
Port[$3c9]:=G div 4;
Port[$3c9]:=B div 4;
End;
Procedure Adjust(xa,ya,x,y,xb,yb: Integer);
Var
d: Integer;
v: Real;
Begin
if plasma[x, y] <> 0 then exit;
d:=Abs(xa - xb) + Abs(ya - yb);
v:=(plasma[xa, ya] + plasma[xb, yb]) / 2 + (random - 0.5) * d * 2;
If v < 1 Then v:=1;
If v >= 255 Then v:=255;
plasma[x, y]:=Trunc(v);
End;
Procedure HalfWay(x1, y1, x2, y2: Integer);
Var
x, y: Integer;
Begin
If (x2 - x1 < 2) and (y2 - y1 < 2) Then Exit;
x:=(x1 + x2) div 2;
y:=(y1 + y2) div 2;
Adjust(x1, y1, x, y1, x2, y1);
Adjust(x2, y1, x2, y, x2, y2);
Adjust(x1, y2, x, y2, x2, y2);
Adjust(x1, y1, x1, y, x1, y2);
If Plasma[x,y]=0 Then
plasma[x,y]:=trunc((plasma[x1, y1] + plasma[x2, y1] +
plasma[x2, y2] + plasma[x1, y2]) / 4);
HalfWay(x1, y1, x, y);
HalfWay(x, y1, x2, y);
HalfWay(x, y, x2, y2);
HalfWay(x1, y, x, y2);
end;
Procedure MakePlasma;
Begin
Plasma[0, 199]:=Random(190);
Plasma[319, 199]:=Random(190);
Plasma[319, 0 ]:=Random(190);
Plasma[0, 0 ]:=Random(190);
HalfWay(0, 0, 319, 199);
End;
Begin
Asm
mov ax ,13h
int 10h
End;
Randomize;
For J:=0 To 43 Do RGB(j, 255, j*6, 0);
For J:=0 To 43 Do RGB(43+j, 255-j*6, 255, 0);
For J:=0 To 43 Do RGB(86+j, 0, 255, j*6);
For J:=0 To 43 Do RGB(129+j, 0, 255-j*6, 255);
For J:=0 To 43 Do RGB(172+j, j*6, 0, 255);
For J:=0 To 40 Do RGB(215+j, 255, 0, 255-j*6);
MakePlasma;
For x := 0 to 319 do
For y := 0 to 199 do
Mem[$0a000 : y * 320 + x] := plasma[x, y];
Readkey;
End.
Чтобы перед глазами все поплыло, мы в цикле будем менять палитру. (Переменная c любого целого типа.)
...
Begin
Asm
mov ax ,13h
int 10h
End;
Randomize;
c:=0;
MakePlasma;
For x := 0 to 319 do
For y := 0 to 199 do
Mem[$0a000 : y * 320 + x] := plasma[x, y];
Repeat
For J:=0 To 43 Do RGB((j+c) mod 256, 255, j*6, 0);
For J:=0 To 43 Do RGB((43+j+c) mod 256, 255-j*6, 255, 0);
For J:=0 To 43 Do RGB((86+j+c) mod 256, 0, 255, j*6);
For J:=0 To 43 Do RGB((129+j+c) mod 256, 0, 255-j*6, 255);
For J:=0 To 43 Do RGB((172+j+c) mod 256, j*6, 0, 255);
For J:=0 To 40 Do RGB((215+j+c) mod 256, 255, 0, 255-j*6);
inc(c);
delay(1000);
Until KeyPressed;
Readkey;
End.
