Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Рассмотрим один из таких фрактальных объектов - триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис. 1.6) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис. 1.6 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным объектом.

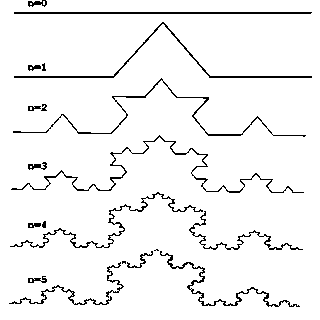
Рис. 1.6. Построение триадной кривой Коха

Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую, называемую снежинкой Коха.

Алгоритм построение фрактала можно описать словесно, как показано на примере построение кривой Коха, либо математически, как будет показано в следующем разделе для алгебраических фракталов. Но существует еще один способ описания алгоритма построения геометрических фракталов с помощью L-систем (системы Линдемайера). L-система это формальная грамматика, используемая для моделирования процессов роста и развития растений.

Изначально L-системы были введены при изучении формальных языков, а также использовались в биологических моделях селекции. С их помощью можно строить многие известные самоподобные фракталы, включая снежинку Коха и ковер Серпинского.

L-система определяется как кортеж G=(V, w, P), где V – алфавит, представляющий набор символов, содержащих элементы которые могут быть представлены графически, w – аксиома, которая представляет собой строку символов из V, определяющая начальное состояния системы, P - представляет собой набор правил производства новой строки, путем замены символов текущего состояния системы на ряд новых. Правила грамматики L-системы применяются итеративно, начиная с начального состояния.

Рассмотрим L-систему, где алфавит состоит всего из двух символов V={a,b}. Аксиома w=a. Правила производства описываются как p1: a→ab, p2: b→ab. Следуя итеративному принципу, каждое поколение кривой удваивается на каждом этапе: a, ab, abab, abababab. Графически a и b отображаются как два равных отрезка, соединенных под прямым углом (рис. 1.7).

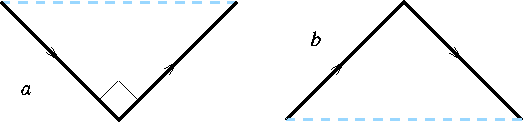
Рис. 1.7. Графическое представление алфавита L-системы

Графическое представление правил p1 и p2, приведено на рис. 1.8. Таким образом, правила описывают замену каждого из отрезков двумя другими, соединенных под прямым углом. При этом, каждый раз, меняется угол поворота новых отрезков относительно исходного.

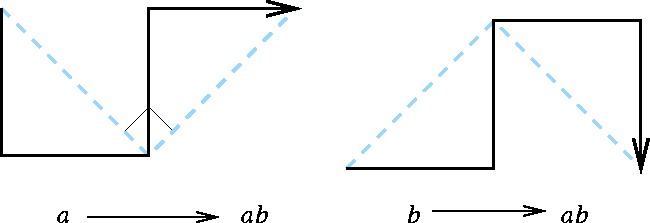
Рис. 1.8. Графическое представление правил L-системы

На рис. 1.9 изображены пять первых итераций процесса построения фрактала.

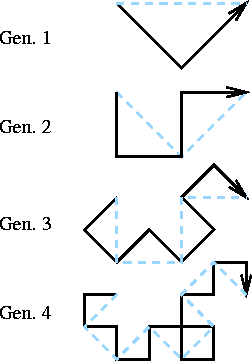
Рис. 1.9. Первые итерации построения фрактальной кривой

Такая предельная фрактальная кривая (при числе итераций стремящимся к бесконечности) называется драконом Хартера-Хейтуэя и представлена на рис. 1.10.

Рис. 1.10. Дракон Хартера-Хейтуэя

Некоторые из геометрических фракталов можно построить исходя из первоначально закрашенной плоской фигуры. Примером этого может служить метод построения треугольника Серпинского. Процесс построения можно описать следующим образом.

Равносторонний треугольник M₀ делится прямыми, параллельными его сторонам, на 4 равных равносторонних треугольника. Из треугольника удаляется центральный треугольник. Получается множество M₁, состоящее из 3 оставшихся треугольников "первого ранга". Поступая точно так же с каждым из треугольников первого ранга, получим множество M₂, состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность M₀, M₁,…, M_n,…пересечение членов которой есть треугольник Серпинского (рис. 1.11).

Рис. 1.11. Построение салфетки Серпинского