Материальная дисперсия

Как указывалось в предыдущем разделе, для расчета времени распро­странения световых импульсов в дисперсионной среде используется групповой показатель преломления N_гр, и групповое время распространения t_гр которое для дисперсионной среды длиной L определяется так:

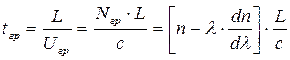. (2.32)

Источник света, как правило, излучает свет не на одной длине волны λ, а со спектральной шириной ∆λ, поэтому отдельные порции света в пределах N_ГР, распространяются с различными скоростями и имеют различные задержки вре­мени.

Если среда распространения дисперсионная и ширина спектра источника излучения составляет ∆λ, то в процессе распространения световой импульс расширяется и поступает на выход среды в течение времени

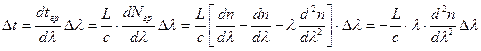. (2.33)

Выражение 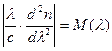называется удельной материальной дисперсией, пс/км∙нм.

Выражение для расчета удельной материальной дисперсии можно полу­чить из (2.28):

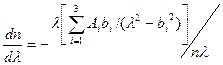, (2.34)

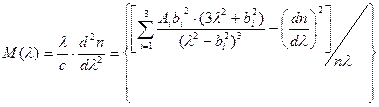. (2.35)

На рис. 2.14 показана зависимость удельной материальной дисперсии. Для чистого кварца на длине волны λ= 0,85 мкм величина М(λ) — 85 пс/км∙нм, при этом с ростом длины волны ее значение уменьшается и проходит через нуль при λ=1,276 мкм.

Таким образом, после прохождения световым импульсом расстояния L в дисперсионной среде он расширяется, причем его длительность т на уровне половинной мощности определяется выражением

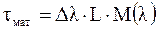. (2.36)

Как видно, уширение импульсов зависит от длины среды и ширины спек­тра источника излучения. И так как ширина спектра излучения у светодиодов значительно больше, чем у лазеров, то и уширение импульсов будет значитель­но больше.

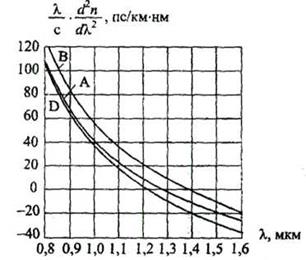
Рис. 2.14. Зависимость удельной материальной дисперсии от длины волны: А - чистый кварц;

В - 13,5% GeO₂,86,5% SiO₂; D - 13,3,% B₂O₃, 86,7% SiO₂

Обычно ширину спектра ∆λ источника излучения определяют как диапа­зон длин волн, в пределах которого излучаемая им мощность превышает 50% максимального значения.

Однако довольно часто используется понятие относительной ширины у спектра излучения источника

,

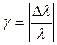тогда после прохождения световым импульсом расстояния L в дисперсионной среде его длительность на уровне половинной мощности

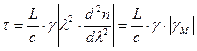, (2.37)

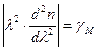- представляет собой коэффициент дисперсии материала.

На рис. 2.15 представлены зависимости коэффициента дисперсии мате­риала Y_мот длины волны для чистого и легированного кварца.

Как видно, кривая Y_м(λ)так же как и М(λ) изменяет знак на длине волны λ = λ₀ = 1,276 мкм. Это значение соответствует точке перегиба кривой п(λ)(рис. 2.10). В литературе часто это значение длины волны определяют как «длину волны нулевой дисперсии материала». С практической точки зрения та­кое определение вводит в заблуждение, так как реальный световой импульс со­держит в себе спектр длин волн, которые распространяются с групповыми ско­ростями, лежащими в некотором интервале, даже если самая короткая и самая длинная волны распространяются с одинаковыми скоростями.

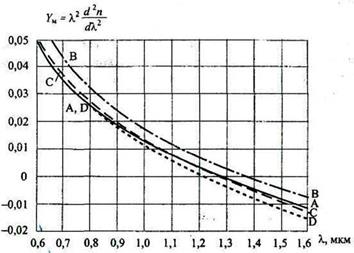
Рис. 2.15. Зависимости дисперсионного параметра Y_м от длины волны: А - чистый кварц; В - 13,5% GeO₂,86,5% SiO₂; С - 9,1% Р₂О₅,90,9% SiO₂; D - 13,3,% В₂О₃,86,7% SiO₂

Для кварца на длине волны λ = λ₀ = 1,276 мкм, Y_м= 0, поэтому

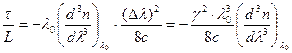. (2.38)

Для чистого кварца на длине волны λ = λ₀ = 1,276 мкм значение 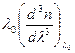= -0,048, следовательно, (2.38) принимает вид, нс/км:

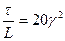. (2.39)

Для светодиодов значение γ= 0,04, поэтому дисперсия τ /L = 32 пс/км.

При использовании лазерных источников излучения значение дисперсии будет на 2 порядка меньше.

Дисперсия материала зависит от его состава. Так, посредством легирова­ния чистого кварца можно изменить ее значение в определенных пределах и тем самым оказать влияние на положение «нулевой точки». Величину λ₀ можно изменить, вводя различные добавки в кварцевое стекло. Как видно из рис. 2.15, введение бора может сделать ее менее 1,22 мкм, а легирование германием по­зволяет поднять ее до 1,37 мкм.

Уширение импульса на длине волны λ₀ в случае с источником с гауссо­вым спектром определяется соотношением

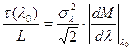, (2.40)

где значение 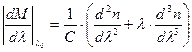определяет наклон кривой удельной дисперсии материала,

, .

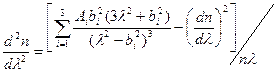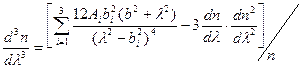Значение коэффициентов А_iи b_iдля стекол различных составов приведены в табл. 2.2. Для

чистого кварца .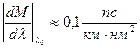

В заключение следует отметить, что длина волны нулевой дисперсии λ₀ = 1,276 мкм соответствует объемной среде. Для оптического волокна эта длина волны сдвигается до значения порядка 1,312 мкм, чем и объясняется ис­пользование источников излучения 1,310 мкм для одномодового волокна.

Межмодовая дисперсия

С точки зрения геометрической оптики световой импульс представляет собой совокупность большого числа лучей света, распространяющихся в серд­цевине ОВ, а с точки зрения волновой теории ─ совокупность множества на­правляемых мод (типов волн).

Различие путей распространения направляемых мод на фиксированной частоте (длине волны) излучения оптического источника приводит к тому, что время прохождения этих мод по ОВ различно. В результате образуемый ими импульс на выходе ОВ уширяется. Величина уширения импульса равна разности времени распространения самой медленной и самой быстрой мод. Указан­ное явление носит название межмодовой дисперсии.

Формулу расчета межмодовой дисперсии можно получить, рассматривая геометрическую модель распространения направляемых мод в ОВ. Любая на­правляемая мода в ступенчатом ОВ может быть представлена световым лучом, который при движении вдоль волокна многократно испытывает полное внутреннее отражение от поверхности раздела «сердцевина-оболочка». Исключени­ем является основная мода НЕ₁₁, которая описывается световым лучом, движу­щимся без отражения вдоль оси волокна.

При длине ОВ (рис 2.16), равной L, длина зигзагообразного пути, прой­денного лучом света, распространяющимся под углом θ_z к оси волокна, состав­ляет L/cos θ_z.

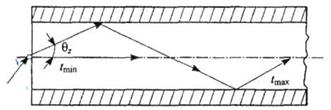
Рис. 2.16. Пути распространения световых лучей в двухслойном ОВ

Скорость распространения электромагнитных волн с длиной волны λоди­накова в рассматриваемом волокне и равна U₁ = с/n₁ , где с - скорость света, км/с. Следовательно, время распространения светового луча в сердцевине ОВ

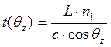. (2.41)

Как видно (2.41), время распространения луча изменяется обратно про­порционально cos θ_z. Значит, минимальное время распространения t_min соответ­ствует θ_z =0, т. е. лучам, распространяющимся параллельно оси, а максималь­ное время распространения t_max соответствует θ_z = θ_кр, где θ_кр - критический угол падения светового луча на границу раздела сердцевина-оболочка.

Таким образом, время распространения по самому длинному и .самому короткому пути согласно (2.41):

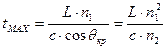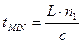; . (2.42)

Пусть на вход ОВ подается очень короткий импульс. Начало выходного импульса совпадает со временем прихода луча, прошедшего самый короткий путь, а конец - со временем прихода луча, прошедшего самый длинный путь.

Следовательно, уширение импульса составит

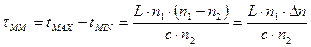. (2.43)

Обычно в ОВ n₁ ≈ n₂, поэтому (2.43) принимает вид

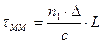, (2.44)

где 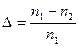- относительное значение показателей преломления сердцевина-оболочка.

Из формулы (2.44) видно, что уширение импульсов, обусловленное межмодовой дисперсией, тем меньше, чем меньше разность показателей преломле­ния сердцевины и оболочки. Это одна из причин, почему в реальных ступенча­тых ОВ эту разность стремятся сделать как можно меньше.

Из (2.44) следует и другой вывод: уширение импульсов пропорционально протяженности ОВ. Однако это справедливо лишь для идеального ОВ, в кото­ром отсутствует взаимодействие между направленными модами. На практике же из-за наличия неоднородностей (главным образом, микроизгибов) отдель­ные моды при прохождении по ОВ воздействуют друг на друга и обмениваются энергией.

Моды низшего порядка с малым углом по отношению к оси ОВ за счет обмена энергией преобразуются в моды высшего порядка с более крутым углом по отношению к оси ОВ и наоборот. Вследствие этого различие скоростей мод выравнивается. В геометрической трактовке это означает, что из-за неоднород­ностей одни и те же лучи изменяют углы, под которыми они распространяются по сердцевине ОВ. При этом изменение углов и задержки компонент сигнала носят случайный характер, а разброс времени распространения мод становится

пропорциональным √L.

Важно отметить, что данное явление проявляется, начиная с определен­ной длины ОВ, которая носит название «длины установившейся связи между модами» - L_y, и зависит от многих случайных факторов, но точно рассчитана быть не может. По данным измерений для ступенчатых ОВ L_y=5─7 км.

Таким образом, межмодовая дисперсия в ОВ со ступенчатым профилем показателя преломления

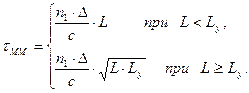(2.45)

Межмодовую дисперсию в ступенчатых ОВ можно полностью исклю­чить, если соответствующим образом подобрать структурные параметры ОВ. Так, если сделать размеры сердцевины и ∆ настолько малыми, то по волокну будет распространяться на несущей длине волны только одна мода, т. е. модовая дисперсия будет отсутствовать. Такие волокна называются одномодовыми. Они имеют наибольшую пропускную способность. С их помощью могут быть организованы большие пучки каналов на магистралях связи.

Дисперсия импульсов может быть также существенно уменьшена за счет соответствующего выбора профиля преломления по сечению сердцевины ОВ. Так, дисперсия уменьшается при переходе к градиентным ОВ. Межмодовая дисперсия градиентных ОВ, как правило, ниже на порядок и более чем у сту­пенчатых волокон.

В таких градиентных ОВ в противоположность ОВ со ступенчатым про­филем распространения, лучи света распространяются уже не зигзагообразно, а по волно- или винтообразным спиральным траекториям (рис 2.17).

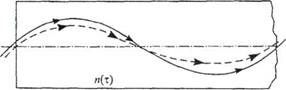
Рис. 2.17. Пути распространения световых лучей в ОВ с параболической зависимостью показателя преломления

Лучи, распространяющиеся вокруг оси ОВ, проходят более длинный путь, чем луч света вдоль оси ОВ. Однако благодаря меньшему показателю преломления в отдалении от оси ОВ, эти лучи распространяются в среде с меньшим п соответственно быстрее, а лучи, распространяющиеся вдоль оси, проходят меньший геометрический путь, но распространяются в среде с боль­шим п, т. е. с меньшей скоростью. В результате время распространения лучей выравнивается, и увеличение длительности импульса становится меньше.

В градиентных многомодовых волокнах время распространения оптиче­ских лучей определяется законом изменения показателя преломления.

Так, межмодовая дисперсия в градиентных ОВ с параболическим профи­лем показателя преломления q_опm = 2, который широко используется па практи­ке, рассчитывается по формуле

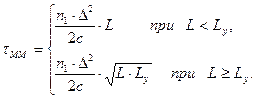(2.46)

При оптимальном профиле показателя преломления q_опm ≈ 2(1 - Δ) дисперсия импульсов минимальна:

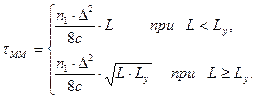(2.47)

По данным измерений значение для градиентного ОB L_y= 10-15 км.

Из сравнения (2.45), (2.46) и (2.47) видно, что межмодовая дисперсия при оптимальном профиле в 8/ Δ раз, а при параболическом в 2/Δ раз меньше, чем при ступенчатом. Например, при одинаковых структурных параметрах ОВ n₁ = 1,46 и ∆_n = 0,015 уширение им­пульсов в ступенчатом световоде со­ставляет 50 нс/км, а в параболическом всего 0,257 нс/км.

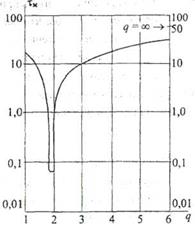
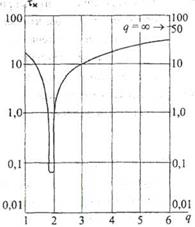
Межмодовая дисперсия τ_ммв гра­диентных ОВ зависит от степени q, по­этому для минимизации дисперсии не­обходимо тщательно подбирать значе­ние q (рис. 2.18).

Изменение профиля, прибли­жающееся к параболическому, суще­ственно уменьшает межмодовую дис­персию в таком градиентном ОВ. Од­нако изготовить оптимальный параболический профиль показателя преломления сложно Наряду с отклонением значения q от требуемого возможно появление осевого провала показателя преломления, пульсаций и других иска­жений профиля, которые на порядок и более увеличивают межмодовую дисперсию. Типичная величина уширения импульсов в полученных ОВ с опти­мальным параболическим профилем составляет 0,2-4,0 не/км.

Рис 2.18. Зависимость τ_м от q

для градиентных ОВ