Входные и выходные данные

СОДЕРЖАНИЕ

Введение. 3

Лабораторная работа №3. 4

Исследование алгоритма шифрования ГОСТ 28147-89. 4

Теоретическое введение. 4

3.1 Краткое описание блоковых шифров…………………………………………………….4

3.2 Структура блоковых шифров……………………………………………………………..4

3.2.1 Входные и выходные данные………………………………………………………4

3.2.2 Сложение с ключом …………………………………………………………………….4

3.2.3 Блок подстановки………………………………………………………………………..5

3.2.4 Блок перестановки……………………………………………………………………….6

3.3 Шифр ГОСТ 28147-89 в режиме простой замены………………………………………6

3.4 Уязвимости ГОСТ 28147-89 в режиме простой замены ……………………………….7

3.5 Контрольные вопросы…………………………………………………………………….8

Пример приложения. 9

Общее задание. 14

Лабораторная работа №4. 14

Построение защиты от несанкционированного копирования. 14

4.1 Введение в защиту от несанкционированного копирования. 14

4.2 Общая схема процедуры установки программы.. 14

4.3 Программные методы защиты от несанкционированного копирования. 15

4.3.1 Защита с помощью пароля…………………………………………………………….15

4.3.2 Привязка к местоположению на диске……………………………………………….16

4.3.3 Запись ключа за логическими пределами файла…………………………………….16

4.3.4 Привязка к параметрам среды………………………………………………………...16

4.3.5 Защита с помощью привязки к другой программе…………………………………..17

4.4 Аппаратные методы защиты от несанкционированного копирования………………18

4.4.1 Защита с помощью ключевой дискеты……………………………………………….18

4.4.2 Защита с помощью ключевого CD/DVD диска……………………………………...18

4.5 Контрольные вопросы…………………………………………………………………...19

Пример приложения. 19

Индивидуальные задания. 26

Список литературы …………………………………………………………………………..27

ВЕДЕНИЕ

Данное методическое указание содержит в себе указания, примеры, общие и индивидуальные задания для выполнения двух лабораторных работ по дисциплине «Информационная безопасность и защита информации». Основной целью данного методического указания является не только практическое рассмотрение и реализация основных вопросов, связанных с защитой информации, но также и попытка закрепления у студентов знаний в области объектно-ориентированного программирования (ООП).

В методических указаниях приведены рекомендации для выполнения двух лабораторных работ, посвященных изучению стандарта шифрования ГОСТ 28147-89

(лабораторная работа №3) и построению защиты от несанкционированного копирования (лабораторная работа №4). Данное методическое указание является практическим приложением к учебно-методическому комплексу (УМК) и должно использоваться студентом при подготовке и выполнении лабораторных работ совместно с УМК. Сначала студент должен изучить теоретический материал в УМК, соответствующий выполняемой лабораторной работе, затем ознакомиться с приведенном в данном методическом указании примером, получить индивидуальный вариант задания у преподавателя и выполнить его. На защите лабораторной работы преподаватель может задать один из контрольных вопросов, приведенных в УМК.

Каждое индивидуальное задание сопровождается примерной оценкой сложности. Оценка сложности указывает на требуемый уровень знания студентом основ программирования и общей подготовки. Шкала имеет мультипликативный вес, т. е. задание, отмеченное как * * * примерно в три раза сложнее задания, отмеченного * и примерно в полтора раза сложнее задания, отмеченного * *.

Лабораторная работа №3

Исследование алгоритма шифрования ГОСТ 28147-89

Теоретическое введение

Краткое описание блоковых шифров

Шифры перестановки и замены сами по себе несостоятельны. Другое дело, если скомбинировать эти два шифра. Тогда не только изменится расположение букв в тексте, но также и сами буквы. К сожалению, криптоанализ также успел развиться, поэтому к современным шифрам предъявляется целый ряд требований. В стандартах разных стран эти требования удовлетворяются различными способами. Но в целом во всем мире наблюдается тенденция построения шифров из отдельных блоков. Мы рассмотрим несколько таких блоков на примере стандарта шифрования Советского Союза ГОСТ 28147-89.

Структура блоковых шифров

Входные и выходные данные

Наличие в заголовке этого параграфа слова «данные» уже говорит о том, что так или иначе мы столкнемся с программированием. Но поскольку данные, шифруемые любым современным блоковым шифром сами по себе нетривиальны, необходимо рассмотреть их. Шифруемый блок данных ГОСТ имеет размер 64 бита и состоит из двух регистров: старшего (L) и младшего (R). И L, и R имеют разрядность 32 бита. Ключ шифрования имеет размер 256 бит. Выходными данными алгоритма простой замены ГОСТ являются регистры L и R, которые опять объединяются в 64-х разрядный блок. Все данные имеют числовой формат.

Поскольку шифруется в основном текстовая информация, требуется некоторое преобразование текстовой информации в числовую. При представлении текста, как правило, используется 8-ми разрядная кодовая таблица ASCII (хотя возможен и вариант с 16-и разрядной таблицей Unicode). Для представления одного символа в ASCII требуется 8 бит (1 байт). Таким образом, мы можем обработать блок в 8 символов (8*8 = 64) за раз. Однако перед тем как перейти к самому шифрованию, нужно еще подготовить данные. На языке ассемблера никаких проблем не возникает из-за особенной гибкости языка в отношении к данным. Любая информация без промежуточных манипуляций представляется в виде числа, и, кроме того, любой большой тип данных представим в виде набора меньших типов данных. Например, 32-х разрядное двойное слово представимо в виде двух 16-и разрядных слов или четырех 8-и разрядных байтов. В языках высокого уровня могут возникнуть некоторые сложности с преобразованием типов. Как правило, они решаются за счет использования встроенных функций преобразования типов, а соединение 8 байтов в одно двойное слово можно произвести за счет последовательного сдвига и сложения.

Сложение с ключом

Обычно применяются несколько вариантов сложения с ключом. Как правило, во всех случаях используется операция сложения по некоторому модулю. В шифре гаммирования (потоковом шифровании) сложение производится по модулю 2. В ГОСТе принято сложение по модулю 2³². До недавнего времени процессоры ЭВМ умели обрабатывать 32-х разрядные числа, но не 64-х разрядные, и это отражено в стандарте. На первый взгляд некоторую сложность может вызвать операция A Mod 2³², потому как наибольшее значение 32-х разрядного числа составляет 2³² – 1. Но если вспомнить свойство операции деления A Mod A = 0, то все проблемы снимаются сами собой. Операция Mod 2³² становится самым обычным сложением. Архитектура микропроцессоров Intel такова, что при переполнении регистра переполняющая единица оказывается во флаге CF регистра флагов процессора. А сам регистр при этом хранит результат операции без переполнившей единицы.

Блок подстановки

В ГОСТе алфавит, применяемый при подстановке, состоит из 16 букв: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. В действительности каждая буква - это число, но поскольку мы говорим об алфавите, корректнее все-таки использовать термин «буква». Кроме того, любой букве может быть поставлен в соответствие код. По этой причине ГОСТ, как и любой другой современный шифр, оперирует числами. В самом ГОСТе не содержится указания на то, какой должна быть таблица замен. Есть только правило, по которому производится подстановка. Сама таблица замен имеет размер 8x16 (8 строк и 16 столбцов) и может, например, иметь вид, приведенный в таблице 3.1.

Таблица 3.1 – Пример таблицы подстановки в ГОСТ 28147-89

Если проанализировать таблицу, можно заметить следующую особенность. В каждой строке ни одно число не повторяется. То есть фактически каждая строка представляет собой случайную перестановку чисел от 0 до 15. Строки нужны для того, чтобы производить замену независимо для каждого заменяемого блока. Встает ряд вполне закономерных вопросов. Почему берутся числа именно от 0 и до 15? Это связано с представлением этих чисел в двоичной системе счисления. Для того чтобы закодировать число 15 нужно четыре двоичных разряда (1111b). Ноль представляется четырьмя двоичными нулями (0000b). Все остальные числа лежат в диапазоне между 0000b и 1111b и целиком заполняют его. Таким образом, получается, что любые четыре бита заменяемой последовательности могут быть заменены по этой таблице. Теперь рассмотрим другой вопрос. Почему в этой таблице 8 строк? Очевидно для того, чтобы заменить восемь 4-битных последовательностей. 4*8 составляет 32 бита. Итого получается, что за один цикл работы таблица может заменить сразу 32 бита заменяемой последовательности. Сама подстановка осуществляется по принципу, приведенному на рисунке 3.1.

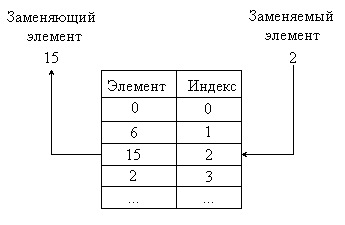
Рисунок 3.1 – Принцип подстановки по ГОСТ 28147-89

В качестве примера взят начальный фрагмент первой строки таблицы 3.1.

В ГОСТ этот блок называется «Подстановка S блока». Фактически она осуществляет многоалфавитную подстановку (для каждого шифруемой тетрады одного блока свой собственный алфавит - строка).

Блок перестановки

В классических шифрах перестановка осуществляется, как правило, по какой-то таблице или аналитическому закону. Однако, очевидно, что это не единственный вариант. С той же задачей может справиться и, например, функция сдвига. Если в качестве сдвигаемой последовательности взять сразу несколько букв (или их кодов) исходного сообщения, можно фактически осуществить их перестановку. В кодовой таблице ASCII каждый символ кодируется 8-битным (байтовым) значением. Следовательно, сдвиг на один байт приведет к смещению всей последовательности на 1 символ. Еще более интересного эффекта можно добиться, если сместить все символы на число бит некратное 8, например, 11. Тогда произойдет не только перемещение самих букв, но также изменяться и их коды, что приведет к дополнительному усилению шифра.