Порядок оценивания курсовой работы
Курсовая работа (типовое задание)
По курсу ИНФОРМАТИКА
на тему:
"ПРИМЕНЕНИЕ ИТ ДЛЯ АНАЛИЗА И ОБРАБОТКИ ДАННЫХ"
Порядок выполнения курсовой работы
Для составление программ используется язык программирования С#.
Отчет сдается в распечатанном виде с подписью студента на титульном листе, также вся работа представляется в электронном виде.
График контрольных мероприятий*
| Этап | № недели |
| Выдача задания на КР | 2-3 |
| 1-я консультация | 7-8 |
| 2-я консультация | 10-11 |
| Сдача КР | 15-16 |
| Защита КР и выставление оценки | Зачетная неделя |
*График может уточняться по договоренности с преподавателем
Задание 1. Найти приближенные значения всех корней уравнения f(x)=0 на отрезке [А,В] с заданной точностью Ɛ.
Построить таблицу функции f(x) на отрезке [А,В], разбив отрезок на n частей.
Определить интервалы локализации корней.
Проверить необходимые и достаточные условия использования заданного метода поиска корней (аналитически) на каждом отрезке и выбрать начальное приближение х0 (если необходимо).
Составить программу нахождения корней с заданной точностью.
Сделать проверку (использовать MathCad, Excel)
Задание 2. Найти приближенное значение определенного интеграла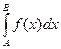 
с заданной относительной погрешностью δ,%.
Составить программу нахождения интеграла с заданным начальным шагом h; затем добиться обеспечения заданной точности.
Сделать проверку по формуле Ньютона-Лейбница (использовать символьные преобразования MathCad)
Задание 3. Решить задачу приближения функции, заданной таблично отрезке [А,В], методом интерполяции.
Составить программу нахождения значения интерполирующей функции в заданной точке x0 отрезка [А,В].
Рассчитать коэффициенты и записать аналитическое выражение для функции на всем отрезке [А,В].
Построить графики исходной (табличной) функции и полученной зависимости (на одном графике.) Сравнить и сделать вывод.
Сделать проверку (использовать MathCad, Excel)
Задание 4. Решить задачу приближения функции, заданной таблично отрезке [А,В], методом аппроксимации с использованием МНК.
Составить систему уравнений для нахождения значений коэффициентов аппроксимирующей функции с использованием метода наименьших квадратов (МНК) (аналитически).
Составить программу нахождения значений коэффициентов аппроксимирующей функции заданным методом решения систем линейных уравнений.
Записать аналитическое выражение для функции с использованием полученных коэффициентов.
Вычислить невязки.
Построить графики исходной (табличной) функции и полученной зависимости (на одном графике.) Сравнить и сделать вывод.
Сделать проверку решения системы уравнений с использованием метода Крамера (Excel)
Проверить полученную зависимость с использованием специальных средств MathCad (например, linfit(x, y, F)), genfit(x, y, v, F))
Задание 5. Составить отчет (использовать MSWord). (Примерный объем 15-25 стр.)
титульный лист
содержание
теоретическое введение
постановка задачи
порядок решения
исходные данные
полученные результаты
выводы
список литературы
Задание 6. Создать презентацию(использовать MS PowerPoint).
Порядок оценивания курсовой работы
Оценка удовлетворительно выставляется студенту при выполнении следующих условий:
· полностью представлены все необходимые материалы по работе: грамотно оформленный отчет и разработанные программные средства;
· студент полностью понимает содержание отчета (используемые методы, необходимые и достаточные условия их использования), может анализировать полученные результаты и интерпретировать их в терминах предметной области;
· студент разбирается в разработанных программных средствах, может объяснить используемые алгоритмы, знает смысл используемых переменных и понимает использованные средства ППП.
Оценка хорошо выставляется студенту при выполнении следующих условий:
· полностью и в срок представлены все необходимые материалы по работе: грамотно оформленный отчет и разработанные программные средства;
· студент полностью понимает содержание отчета (используемые методы, необходимые и достаточные условия их использования), может анализировать полученные результаты и интерпретировать их в терминах предметной области; при этом также может проводить сравнительный анализ методов по каждой области применения.
· студент разбирается в разработанных программных средствах, может объяснить используемые алгоритмы, знает смысл используемых переменных и понимает использованные средства ППП и может объяснить выбор того или иного средства.
Оценка отлично выставляется студенту при выполнении следующих условий:
· полностью и в срок представлены все необходимые материалы по работе: грамотно оформленный отчет и разработанные программные средства;
· студент свободно владеет вопросами, которым посвящена КР (используемые методы, необходимые и достаточные условия их использования и сравнительная характеристика), может анализировать полученные результаты и интерпретировать их в терминах предметной области, а также аргументированно вести обсуждение используемых средств;
· студент разбирается в разработанных программных средствах, может объяснить используемые алгоритмы, знает смысл используемых переменных и понимает использованные средства ППП, может объяснить выбор того или иного средства. Алгоритмы разработаны на основе метода пошаговой детализации, при написании программ используются дополнительные средства С#, такие как методы, работа с файлами, графический интерфейс и т.д.
ВАРИАНТЫ ЗАДАНИЙ
Задания 1-2 выполняются с использованием функции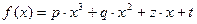 
, где p = 1; q = -(a+b+c); z= a∙b+a∙c+b∙c; t = -a∙b∙c.
В Задании 3 используется только таблица функции f(x) (полученная при выполнении Задания 1). В качестве точки для получения интерполяционного значения взять х0=(А+В)/2+0,24.
Для всех вариантов принять Ɛ=10-4
Для всех вариантов принять δ=0.3%
Для всех вариантов принять h=1
При невозможности использования указанного метода поиска корней (Задание 1), использовать метод дихотомии
| № вар. | A | B | a | b | c | n | № мет. Зад.1 | № мет. Зад.2 | № мет. Зад.3 | № Зад.4 | № мет. Зад.4 |
| -1 | -0,3 | 1,1 | 4,22 | 1a | |||||||
| -2,16 | 5,12 | -1 | 0,67 | 3,14 | 1b | ||||||
| -0,8 | -0,92 | 5,4 | 2a | ||||||||
| -3 | 4,5 | -2,1 | -2,1 | 3,3 | 2b | ||||||
| -6 | 1,15 | -4,11 | -2,5 | -2,5 | 3a | ||||||
| 0,5 | 6,9 | 3b | |||||||||
| 7,2 | 0,9 | 7,1 | 4a | ||||||||
| -2 | 5,14 | -1 | 4,1 | 4b | |||||||
| -3 | 4,22 | 5a | |||||||||
| -2 | 4,4 | 1,5 | 1,5 | 2,14 | 5b | ||||||
| -7 | 1,1 | -1 | 0,98 | 0,87 | 6a | ||||||
| -0,1 | 9,4 | 0,9 | 2,16 | 8,18 | 6b | ||||||
| 2,4 | -3,12 | 0,6 |
Список методов для Задания 1
1. Метод итераций
2. Метод касательных (Ньютона)
3. Метод секущих
4. Метод хорд
Список методов для Задания 2
1. Метод прямоугольников с вычислением высоты прямоугольника на левом конце отрезка
2. Метод прямоугольников с вычислением высоты прямоугольника на правом конце отрезка
3. Метод прямоугольников с вычислением высоты прямоугольника в середине отрезка
4. Метод трапеций
5. Метод Симпсона
Список методов для Задания 3
1. Линейная интерполяция
2. Квадратичная интерполяция
Список методов для Задания 4
1. Метод Гаусса
2. Метод Гаусса с выбором главного элемента
3. Метод прогонки
Варианты задач для Задания 4
1.Технически чистая медь ε = 20%, t = 6000C.
| u, сек-1 | 0,01 | 0,05 | 0,10 | 0,50 | 1,0 | 1,5 | |||||
| σв, кг/мм2 | 7,2 | 7,6 | 7,9 | 8,1 | 8,9 | 9,9 | 10,8 | 12,0 | 13,3 | 14,7 | 16,2 |
a. линейная φ0(u)=1; φ1(u)=u; φ2(u)=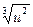 
; φ3(u)=arctg u
b. нелинейная σв(u,a)=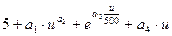 
2. Технически чистая медь ε = 20%, t = 2000C.
| u, сек-1 | 0,01 | 0,05 | 0,10 | 0,50 | 1,0 | 1,5 | |||||
| σв, кг/мм2 | 16,6 | 17,1 | 17,7 | 18,0 | 18,8 | 19,3 | 20,0 | 21,2 | 22,0 | 23,4 | 25,1 |
a. линейная φ0(u)=1; φ1(u)=u2; φ2(u)=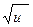 
; φ3(u)=arctg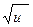
b. нелинейная σв(u,a)=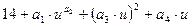 
3. Сталь X18H9T. ε = 20%, t = 12000C.
| u, сек-1 | 0,1 | 0,4 | 1,0 | 2,0 | 6,0 | 10,0 | 20,0 | 40,0 | 60,0 | 80,0 | 100,0 |
| σв, кг/мм2 | 6,6 | 7,0 | 7,5 | 7,9 | 8,4 | 8,8 | 9,3 | 10,1 | 10,7 | 11,3 | 11,7 |
a. линейная φ0(u)=1; φ1(u)=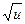 
; φ2(u)= 
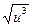; φ3(u)=cos(1+ )
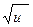b. нелинейная σв(u,a)=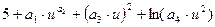 
4. Сталь X18H9T. ε = 20%, t = 10000C.
| u, сек-1 | 0,1 | 0,4 | 1,0 | 2,0 | 6,0 | 10,0 | 20,0 | 40,0 | 60,0 | 80,0 | 100,0 |
| σв, кг/мм2 | 10,9 | 11,8 | 12,8 | 13,4 | 14,6 | 15,3 | 16,4 | 17,7 | 18,5 | 19,2 | 19,9 |
a. линейная φ0(u)=1; φ1(u)=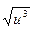 
; φ2(u)= 
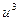; φ3(u)=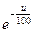 
b. нелинейная σв(u,a)=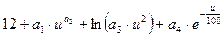 
5. Катаный молибден
| t, 0C | |||||||||||
| σв, кг/мм2 |
a. линейная φ0(t)=1; φ1(t)=t2; φ2(t)= 
; φ3(t)=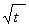 
b. нелинейная σв(t,a)=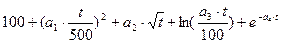 
6. Катаный молибден
| t, 0C | |||||||||||
| δ, % | 7,5 | 5,5 | 2,5 |
a. линейная φ0(t)=6; φ1(t)=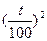 
; φ2(t)= 
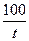; φ3(t)=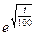 
b. нелинейная δ(t,a)= 
7.
| x | |||||
| y | 2.9 | 8.9 | 19.1 | 33.2 | 50.8 |
f(x)=a∙x2+b∙x+c
Список рекомендуемой литературы
| 1. Светозарова Г.И Андреева О.В. Информатика. Раздел: Основы программирования на языке Турбо-Бейсик и численные методы. Учебное пособие. М. Из-во «Учеба», 2008. – 127 с. |
| 2. Светозарова Г.И., Бесфамильный М.С., Андреева О.В. Информатика. Прикладные программы в среде Windows. Текстовый редактор Microsoft Word 2000. Лабораторный практикум. М. Из-во «Учеба», 2003. -62 с. |
| 3. Сигитов Е.В. Информатика. Раздел: Электронные таблицы Excel. Лабораторный практикум. М., МИСиС,2008.- 106 с. |
| 4. Гопенгауз В.И., Кудрявцев Ю.А. Информатика. Раздел: Прикладные прграммы в пакете MathCad 2000 Professional. Лабораторный практикум. М. Из-во «Учеба», 2006.- 67с |
| 5. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. - Томск: МП "РАСКО", 1991. - 272 с: ил. |
| 6. Колесников А. П."Методы численного анализа, изложенные на языке формул и алгоритмическом языке С#". М.: ЛИБРОКОМ, 2013 - 416 с |