Ручные вычисления поставленной задачи
Теория графов.
Деревья и прадеревья.
з дисципліни "Дискретні структури"
ХАІ.603.622П.13О.050103.126334.ПЗ
Виконав: студент гр. 622П Бровко В.К.
________ , 19.11.2013 (№ групи) (П.І.Б)
(підпис)
Перевірив: к.т.н., доц. Труш Г.О.
(наукова ступінь, вчене звання) (П.І.Б)
________ , 19.11.2013
(підпис)
Цель работы: изучить метод перерасчета прадеревьев и метод пересчета частичных деревьев для графа.
Постановка задачи:
1. Ознакомиться с приведенными теоретическими понятиями о деревьях и прадеревьях графов.
2. Изучить понятия прадерево и частичное дерево графа, а также способы их нахождения с помощью приведенных примеров.
3. Решить вручную задачу пересчета прадеревьев (или частичных деревьев) для графа своего варианта.
4. Написать программу (в произвольно выбранной среде программирования), которая реализует пересчет прадеревьев (частичных деревьев) графа.
Вариант №1
Найти все прадеревья данного графа:
Ручные вычисления поставленной задачи
1. Составим матрицу смежности графа (матрица ||a||):
| A X1 | B X2 | C X3 | D X4 | E X5 | F X6 | G X7 | |
| A(X1) | |||||||
| B(X2) | |||||||
| C(X3) | |||||||
| D(X4) | |||||||
| E(X5) | |||||||
| F(X6) | |||||||
| G(X7) |
2. Составим матрицу (входящих) связей вершин графа (матрица ||d||):
| A X1 | B X2 | C X3 | D X4 | E X5 | F X6 | G X7 | |
| A(X1) | |||||||
| B(X2) | |||||||
| C(X3) | |||||||
| D(X4) | |||||||
| E(X5) | |||||||
| F(X6) | |||||||
| G(X7) |
3. Поэлементно вычтем матрицу ||d|| из матрицы ||a||, получим матрицу ||b||:
| A X1 | B X2 | C X3 | D X4 | E X5 | F X6 | G X7 | |
| A(X1) | -1 | -1 | |||||
| B(X2) | -1 | -1 | -1 | ||||
| C(X3) | -1 | -1 | |||||
| D(X4) | -1 | ||||||
| E(X5) | -1 | -1 | |||||
| F(X6) | -1 | ||||||
| G(X7) | -1 | -1 |
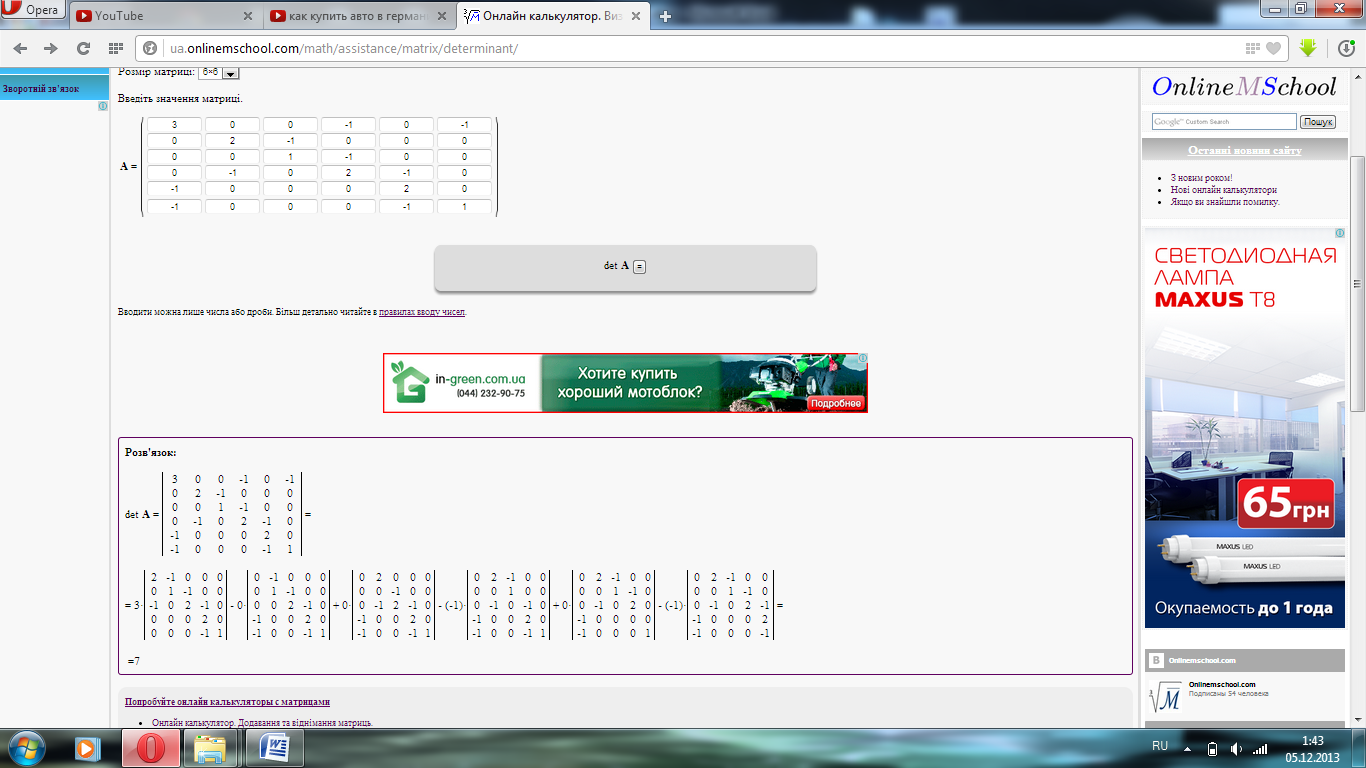
4. Вычеркнем первую вершину A(X1) из матрицы ||b||, подсчитаем минор полученной матрицы, используя математический ресурс
http://ua.onlinemschool.com/math/assistance/matrix/determinant/:
| B X2 | C X3 | D X4 | E X5 | F X6 | G X7 | |
| B(X2) | -1 | -1 | ||||
| C(X3) | -1 | |||||
| D(X4) | -1 | |||||
| E(X5) | -1 | -1 | ||||
| F(X6) | -1 | |||||
| G(X7) | -1 | -1 |
Минор данной матрицы равен 7. Т.к. количество прадеревьев (или частичных деревьев) графа равно значению минора матрицы, то для данного графа можно построить 7 прадеревьев.
Вывод: выполняя данную работу, я изучил метод перерасчета прадеревьев и метод пересчета частичных деревьев для графа, научился находить минор матрицы и программно реализовал данные вычисления (алгоритм Гаусса).
Машинный листинг программы
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace LR5
{
class Program
{
// Генерация массива
static private int[][] initArray()
{
int[][] mat = new int[7][];
mat[0] = new int[7] { 0, 1, 1, 0, 0, 0, 0 };
mat[1] = new int[7] { 1, 0, 0, 0, 1, 0, 1 };
mat[2] = new int[7] { 1, 0, 0, 1, 0, 0, 0 };
mat[3] = new int[7] { 0, 0, 0, 0, 1, 0, 0 };
mat[4] = new int[7] { 0, 0, 1, 0, 0, 1, 0 };
mat[5] = new int[7] { 0, 1, 0, 0, 0, 0, 0 };
mat[6] = new int[7] { 0, 1, 0, 0, 0, 1, 0 };
return mat;
}
// Возвращает ||d|| матрицу
static private int[][] getDMatrix(int[][] a)
{
int[][] d = new int[a.Length][];
int i, j, s;
for (i = 0; i < a.Length; i++)
{
s = 0;
d[i] = new int[a[i].Length];
for (j = 0; j < a[i].Length; j++)
{
d[i][j] = 0;
s += a[j][i];
}
d[i][i] = s;
}
return d;
}
// Разница матриц
static private int[][] subtractMatrix(int[][] a, int[][] b)
{
int[][] x = new int[a.Length][];
int i, j;
for (i = 0; i < a.Length; i++)
{
x[i] = new int[a[i].Length];
for (j = 0; j < a[i].Length; j++)
x[i][j] = a[i][j] - b[i][j];
}
return x;
}
// Вывод матрицы на экран
static private void outMatrix(int[][] x)
{
int i, j;
for (i = 0; i < x.Length; i++)
{
for (j = 0; j < x[i].Length; j++)
Console.Write(" " + x[i][j]);
Console.WriteLine();
}
Console.Write("\n");
}
// 2 функции для определения детерминанта матрици
// по какому-то не известному мне алгоритму
// Нахождение определителя введённой матрицы
static private double det(double[][] matrix)
{
double ratio, det;
int i, j, k, n = matrix.Length;
/* Приобразование матрицы к верхней треугольной */
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
if (j > i)
{
ratio = matrix[j][i] / matrix[i][i];
for (k = 0; k < n; k++)
{
matrix[j][k] -= ratio * matrix[i][k];
}
}
}
}
det = 1; //хранилище определителя
for (i = 0; i < n; i++)
det *= matrix[i][i];
return det;
}
// заглушка для определителя
static private double det(int[][] matrix)
{
int i, j;
double[][] r = new double[matrix.Length][];
for (i = 0; i < matrix.Length; i++)
r[i] = new double[matrix[i].Length];
for (i = 0; i < matrix.Length; i++)
for (j = 0; j < matrix.Length; j++)
r[i][j] = matrix[i][j] * 1.0;
return det(r);
}
// Удаление n-го элемента из матрицы
static int[][] minor(int[][] a, int n)
{
int i, j;
int[][] r = new int[a.Length - 1][];
for (i = 0; i < a.Length; i++)
{
if (i < n) r[i] = new int[a[i].Length - 1];
if (i > n) r[i - 1] = new int[a[i].Length - 1];
}
int x, y;
if (n > 0)
for (i = 0; i < a.Length; i++)
for (j = 0; j < a[i].Length; j++)
{
if (i < n) x = i;
else x = i - 1;
if (j < n) y = j;
else y = j - 1;
r[x][y] = a[i][j];
}
else
for (i = 1; i < a.Length; i++)
for (j = 1; j < a[i].Length; j++)
r[i - 1][j - 1] = a[i][j];
return r;
}
static void Main(string[] args)
{
int[][] a, d, b;
a = initArray();
d = getDMatrix(a);
b = subtractMatrix(d, a);
Console.WriteLine("Матрица ||a||");
outMatrix(a);
Console.WriteLine("\nМатрица ||d||");
outMatrix(d);
Console.WriteLine("\nМатрица ||b||");
outMatrix(b);
int el = 0;
Console.WriteLine("Введите вершину, от которой нужно найти количество прадеревьев (0-7) : ");
el = int.Parse(Console.ReadLine()) - 1;
Console.WriteLine("\nМинор по " + (el + 1) + " вершине:");
b = minor(b, el);
outMatrix(b);
Console.WriteLine("\nКоличество прадеревьев, исходящих из " + (el + 1) + " вершины : " + det(b));
Console.Read();
}
}
}
