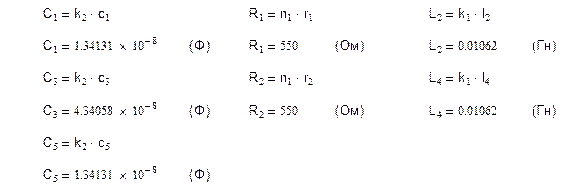На данном этапе по найденной ранее функции Т(р) необходимо получить схему ФНЧ.

Существует несколько способов реализации электрических фильтров: по Дарлингтону, ускоренный метод реализации симметричных и антиметричных фильтров Попова П.А., реализация по каталогу нормированных схем и т.д. Реализация по Попову основана на формировании функции Z_вх(р) по Т(р). Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции Z_вх(р) в цепную дробь (по Кауэру).

Для каждой пары комплексно – сопряженных корней р(к) полинома V(p) передаточной функции Т(р) (полученной на этапе аппроксимации) составим элементарный множитель Нк :Н_к = (р – р(к))(р – р(к)*) = р² + 2σ_кр + σ_к² + Ω_к²

где р(к) = -σ_к + jΩ_к , р(к)^* = -σ_к - jΩ_к .

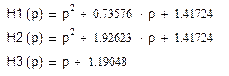
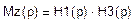Сформируем полином Мz(p) как произведение элементарных сомножителей H_к с нечетными индексами

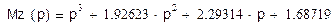
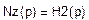Сформируем полином Nz(p) как произведение элементарных сомножителей Н_к с четными индексами:

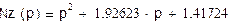
Определим Kz из условия

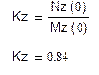
Составим функцию Zвх (р) по формуле:

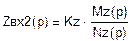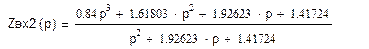
Разложим полученную функцию в цепную дробь по Кауэру

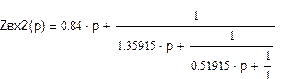
и построим нормированную схему правой половины фильтра (рис.1)

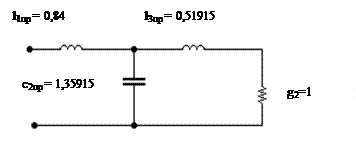
Рис.1 Нормированная схема правой половины фильтра

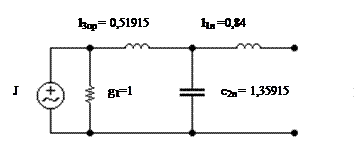Реализуем левую половину фильтра в соответствии с условием симметрии Z _вых1 = Z_вх2 (рис.2)

Рис.2 Нормированная схема левой половины фильтра

После объединения левой и правой половин и замены источника тока на эквивалентный источник напряжения, получим полную нормированную схему фильтра (рис.3).

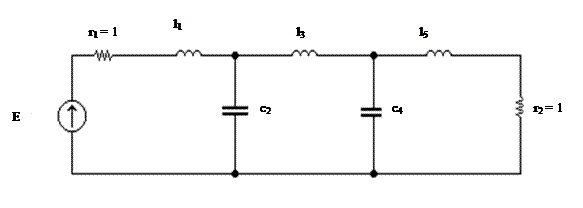
Рис.3 Полная нормированная схема фильтра

l₁ = l_3л = 0.5191475 с₂ = с_2л = 1.3591457

l₃ = l_1л + l_1пр = 1.6799965 с₄ = с_2пр = 1.3591457

l₅ = l_3пр = 0.5191475

Получим дуальную схему фильтра (рис.4)

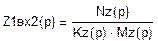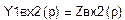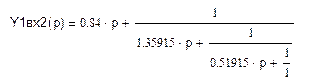
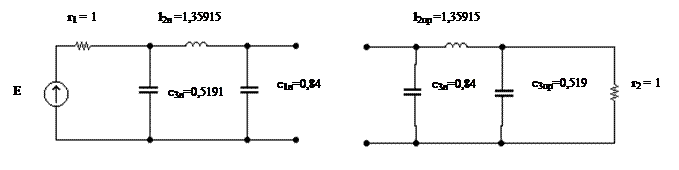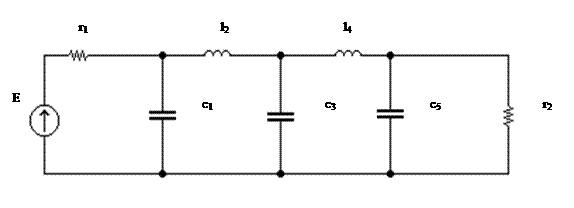
Рис.4 Дуальная схема фильтра

c₁ = c_3л = 0.5191475 l₂ = l_2л = 1.3591457

c₃ = c_1л + c_1пр = 1.6799965 l₄ = l_2пр = 1.3591457

c₅ = c_3пр =0.5191475 r₁ = r₂ = 1

Денормирование по частоте

Осуществим переход от нормированной схемы ФНЧ к схеме заданного фильтра согласно [1]. Причем выберем наиболее экономичную (с меньшим числом индуктивностей ) (рис.5)

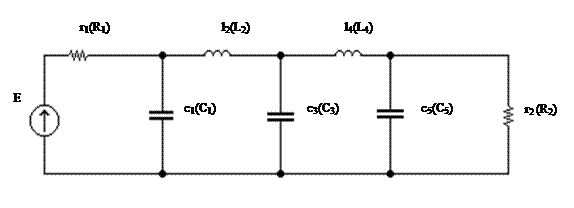Рис.5 Схема заданного фильтра

Для перехода к денормированным нагрузочному сопротивлению R₂ и граничной частоте f₂ ( т. к. ФНЧ) осуществляется изменение уровня сопротивления и масштаба частоты с помощью следующих множителей:

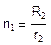а) преобразующий множитель сопротивления:

где R₂ - нагрузочное сопротивление,

r₂ - нормированное нагрузочное сопротивление;

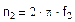б) преобразующий множитель частоты:

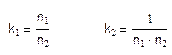Коэффицикнты денормирования индуктивности k₁ и емкости k₂ определяются по формулам:

Рассчитаем эти коэффициенты:

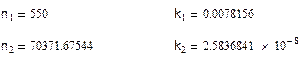
Денормированные значения заданного фильтра определяются по следующим формулам: