Информация и её кодирование

ВАРИАНТ 18

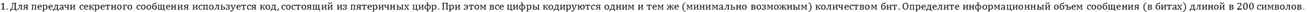
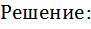
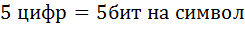
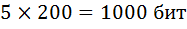
2. Какое наименьшее количество символов должно быть в алфавите, чтобы при помощи всевозможных четырехбуквенных слов данного алфавита, можно было передать не менее 250 различных сообщений?

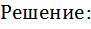
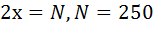
Берем степень 2-ки при которой получается чисто больше 250, но близкое к нему:

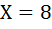
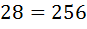
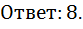
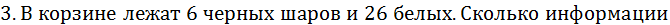
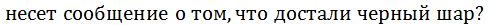
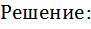
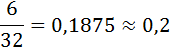
Log₂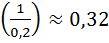

Ответ: .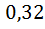

4. Определите количество информации в сообщении «БЕГЕМОТ» с учетом и без учета вероятности появления символов в сообщении, определите энтропию и избыточность алфавита в сообщении.

Решение:

N=7

I=log₂7 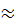2,8бит

1) p_б=1/7 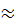0,143

2) р_е=2/7 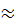0,29

3) p_г=1/7 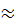0,143

4) p_м=1/7 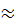0,143

5) p_о=1/7 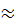0,143

6) p_т=1/7 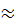0,143

7) i_б=log₂(1/0,143) 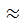2,8бит

8) i_е=log₂(1/0,29) 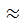1,79бит

9) i_г=log₂(1/0,143) 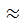2,8бит

10) i_м=log₂(1/0,143) 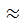2,8бит

11) i_о=log₂(1/0,143) 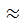2,8бит

12) i_т=log₂(1/0,143) 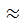2,8бит

I=1*2,8+2*1,79+1*2,8+1*2,8+1*2,8+1*2,8=17,58бит

H( 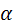)=-(5*0,143*log₂(0,143)+0,29*log₂(0,29))=2,5бит

D=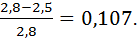

Ответ: 0,107.

5. Определите время (в секундах) передачи файла размером 5 Мб по каналу связи со скоростью 512000 бит/с.

Решение:

2⁹=512

5Мб=5×2²³бит

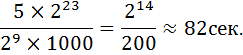
Ответ:82 сек.

6. Дано а=С9,5₍₁₆₎,b=345,45₍₈₎. Выполнить действие а+b ответ представить в 16-й системе счисления.

Решение:

С9,5₍₁₆₎=12×16+9×16⁰+5×16^-1=192+9+0,3125=201,3125₍₁₀₎

345,45₍₈₎=3×8²+4×8+58⁰+4×8^-1+5×8^-2=192+32+0,5+0,078125=229,57812₍₁₀₎

201,3125+229,57812=430,89062₍₁₀₎

430 16 0,89062×16=14,24992

416 26 16 0,24992×16=3,99872

16 1 0,99872×16=15,97951

10 Е3F

1АЕ

Ответ: 1АЕ,Е3F.

7. Дано а=6С3,45₍₁₆₎, b=24₍₈₎. Выполнить действие а-b ответ представить в 8-й системе счисления.

Решение:

6С3,45₍₁₆₎=6×16²+12×6+3×16⁰+4×16^-1+5×16^-2 =1536+192+192+3+0,25+0,01953125=1731,2695₍₁₀₎

332,25₍₈₎=192+24+2+0,25+0,078125=218,3281₍₁₀₎

1731,295-218,3281=152,9559₍₁₀₎

Переводим из 10 системы счисления в 8-ю:

152 0 0,9669×8=7,7352

189 5 0,7352×8=5,8816

23 7 0,8816×8=7,0528

Ответ:750,757.

8. Дано а=31А₍₁₆₎, b=24₍₈₎ . Выполнить действие a×b ответ представить в 2-й системе счисления.

Решение:

31А₍₁₆₎=1100011010₍₂₎

24₍₈₎=10100₍₂₎

× 10100

11111000001000 ₍₂₎

Ответ: 11111000001000 ₍₂₎

9. Получить десятичное представление заданного числа а=0001000000010111₍₂₎.

0001₍₂₎=1₍₁₀₎

0000₍₂₎=0₍₁₀₎

0001₍₂₎=1₍₁₀₎

0111₍₂₎=1+1×2¹+1×2²=7₍₁₀₎

Ответ:1017₍₁₀₎.

10. Запишите прямой, обратный и дополнительный код а=173₍₁₀₎ числа в шестнадцатиразрядном представлении.

Решение:

173₍₁₀₎→₍₂₎

173 1 10101101₍₂₎

86 0 переводим, 1меняем на 0,а 0 на 1:

43 1 0000000010101101

21 1 Ответ: 0000000010101101

10 0

5 1

2 0

11. Восстановить десятичное представление целого числа по его коду1110110101100100₍₂₎ .

1110110101100100₍₂₎

1

Переводим 0001001010011100

Переводим в десятичную систему счисления:

0001001010011100₍₂₎=1×2²+1×2³+1×2⁴+1×2⁷+1×2⁹+1×2¹²= -4764

Ответ: -4764.

12. Запишите код вещественного числа -122,35₍₁₀₎ в формате с плавающей запятой одинарной точности.

Решение:

13. Каждый символ в UNICODE закодирован двух байтовым словом. Оцените информационный объем следующего предложения в этой кодировке: «Не бойтесь того, что ваша жизнь должна окончиться, бойтесь того, что она так и не начнется».

Решение:

88символов

88×2=176байт

Ответ:176байт.

14. Сообщение на русском языке первоначально было записано в 16-битном коде UNICODE. Автоматическое устройство осуществило перекодировку в кодировку WINDOWS 1251. При этом информационное сообщение уменьшилось на 140 байт. Определите длину сообщения в символах.

Решение:

16х=8х+1120

8х=1120

х=140.

Ответ: 140.

15. Какое минимальное количество бит потребуется для кодирования любого цвета из палитры, насчитывающей 300 различных цветов?

Решение:

2ⁿ=300

n=9бит.

Ответ: 9.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Информатика и программное обеспечение»

ИНФОРМАЦИЯ И ЕЁ КОДИРОВАНИЕ

РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА №1

Всего 6 листов

Руководитель

Зернин М.В.

«___»____________2012 г.

Студент гр. 12-ТБ

Сякина М.А.

«___»____________2012 г.

БРЯНСК 2012.