Вычисление интегральной функции

Вернемся к нашей табличной функции .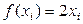

xi		0.2	0.4	0.6	0.8		1.2	1.4	1.6
f(xi)		0.4	0.8	1.2	1.6		2.4	2.8	3.2

Напомним, что неопределенный интеграл от функции 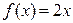есть функция (константой С пока пренебрегаем). Давайте получим эту зависимость.

Рассмотрим случай когда:

Введем величину :

Как видите, для i-ой точки эта величина равна значению определенного интеграла от x₁ до x_i.

Пройдясь по всему диапазону, на котором определена наша табличная функция, мы получим следующую последовательность значений для .

xi		0.2	0.4	0.6	0.8		1.2	1.4	1.6
f(xi)		0.4	0.8	1.2	1.6		2.4	2.8	3.2
			0.08	0.16	0.24	0.32	0.4	0.48	0.56
			0.08	0.24	0.48	0.8	1.2	1.68	2.24

На рис. 22 представлен график построеный по значениям . Для сравнения пунктиром показан график реальной параболы.

Рис. 22

Данный рисунок хорошо демонстрирует тот факт, что численные методы обладают определенной погрешностью. Естественно возникает вопрос можно ли повысить точность вычислений или, иначе говоря, уменьшить эту погрешность? Ответ на данный вопрос будет рассмотрен в следующей лабораторной работе.

Решение типовых задач

Задача 1. Дана табличная функция . Найти значение определенного интеграла на интервале на интервале [a,b].

Решение.

Используем данные, полученные в лабораторной работе №6 при вычислении производной функции Пример чтения данных из файла был описан в листинге 26 и здесь не приводится.

Листинг 36

/*Определенный интеграл*/

#include <fstream.h>

#include <math.h>

void main( void )

{

// Массив для хранения значений аргумента и функции

double nArray[11][2];

// Прочитать данные табличной функции из файла,

// занести их в массив nArray и вывести на экран (Листинг 26)

double dSumLeft = 0, dSumRight = 0;

// Вычисляем суммарную площадь для случаев выбора точки

// слева и справа относительно частичного интервала.

for (int i = 1; i < 11; i++ )

{

dSumLeft = dSumLeft+nArray[i-1][1] * (nArray[i][0] - nArray[i-1][0]);

dSumRight = dSumRight+nArray[i][1] * (nArray[i][0] - nArray[i-1][0]);

}

// Вывод результата

cout << "\n\nSumLeft = " << dSumLeft << "\n";

cout << "SumRight = " << dSumRight << "\n";

}

Задача 2. Дана табличная функция . Найти значения найти значения для функции неопределенного интеграла. Занести полученные данные в файл. Построить график интегральной функции.

Решение.

Как и в предыдущей задаче воспользуемся данными, полученными в лабораторной работе №6 при вычислении производной функции . Программный код, осуществляющий чтение приводить не будем. Считаем, что данные прочитаны и занесены в массив nArray.

Листинг 30

/*Неопределенный интеграл*/

#include <fstream.h>

#include <math.h>

void main( void )

{

// Массив для хранения значений аргумента и функции

double nArray[11][2];

// Прочитать данные табличной функции из файла,

// занести их в массив nArray и вывести на экран (Листинг 26)

// Вывод заголовка

cout << "\nIntegral\nx\ty_left\ty_right\n";

// Массив для хранения результата

double dResultLeft, dResultRight;

ofstream File("integral.txt");

dResultLeft = 0; dResultRight = 0;

for ( i = 1; i <= 10; i++ )

{

dResultLeft=dResultLeft+nArray[i-1][1]*(nArray[i][0] - nArray[i-1][0]);

dResultRight=dResultRight+nArray[i][1]*(nArray[i][0] - nArray[i-1][0]);

// Вывод результата на экран

cout << nArray[i][0]<<"\t"<<dResultLeft<<“\t”<<dResultRight<<"\n";

// Вывод результата в файл

File << nArray[i][0]<<"\t"<<dResultLeft<<“\t”<<dResultRight<<"\n";

}

File.close();

}

Содержимое файла integral.txt:

0.2 0 0.08

0.4 0.08 0.24

0.6 0.24 0.48

0.8 0.48 0.8

1 0.8 1.2

1.2 1.2 1.68

1.4 1.68 2.24

1.6 2.24 2.88

1.8 2.88 3.6

2 3.6 4.4

График интеграла представлен на рис. 23

Рис. 23

Задание на лабораторную работу №9

Задача 1. Используя табличные данные производной функции, полученные в лабораторной работе №6, разработать алгоритм и написать по нему программу вычисления определенного интеграла функции. Результат вывести на экран.

Задача 2. Используя табличные данные производной функции, полученные в лабораторной работе №6, разработать алгоритм и написать по нему программу вычисления значений интегральной функции. Результат вывести на экран и в текстовый файл. Построить графики исходной табличной функции и графики ее интегральных функций.

Оформить протокол лабораторной работы.

Примечание! Алгоритмы решения задач должны содержать не только расчетную часть, но и блоки формирования входных и выходных данных, а также блоки проверки правильности вводимых данных.

Контрольные вопросы

1. В чем разница между определенным и неопределенным интегралами?

Лабораторная работа №10

Цель: усовершенствовать навыки программирования на примере решения вычислительных задач с заданной точностью.

Задачи:

Разработать алгоритм и написать по нему программу определения с заданной точностью значения определенного интеграла табличной функции.