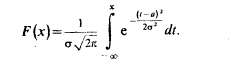Вероятность попадания случайной величины в заданный интервал с помощью интегральной функции распределения
Вероятность того, что случайная величина Х примет значение из промежутка (а,в), вычисляется по формуле: Р(а < X < b) = F(b) – F(а).
Плотность вероятности непрерывной случайной величины, ее вероятностный и геометрический смысл и свойства.
Примеры основных распределений дискретной случайной величины.
Вероятность попадания непрерывной случайной величины в заданный интервал (с помощью дифференциальной функции распределения).
Числовые характеристики дискретных случайных величин .
. Мат ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений:
2. Дисперсия с.в. Х – это мат ожидание квадрата отклонения случайной величины от своего математического ожидания:
DX=D(X) = M[X-M(X)]2 = M(X2) – (MX)2 = M(X2) – m(x)2
3. ?Дисперсия имеет размер квадрата с.в. для наглядности в качестве характеристики рассеивания удобного использования числом?
Среднее квадратическое отклонение (стандартное отклонение) случайной величины –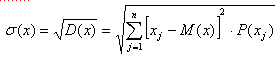 
Числовые характеристики непрерывных случайных величин.
Основные свойства математического ожидания и дисперсии.
Свойства математического ожидания.
1. Математическое ожидание неслучайной величины с равно самой величине с:
M[c] = c. (6.4)
Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1:
M[c]=c∙1=c.
2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание:
M[c×X] = c×M[X]. (6.5)
Доказательство:
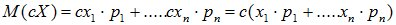
3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:
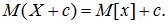(6.6)
Доказательство: следует из свойств 1 и 3.
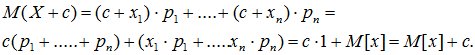
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M[X+Y] = M[X]+M[Y]. (6.6)
Свойства дисперсии
Дисперсия постоянной величины с равна нулю.
Доказательство: по определению дисперсии
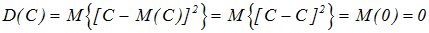
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.
D[X+c] = D[X].
Доказательство: по определению дисперсии
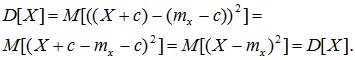(6.12)
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.
Доказательство: по определению дисперсии
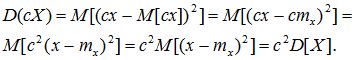. (6.13)
Для среднего квадратичного отклонения это свойство имеет вид:
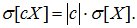(6.14)
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е.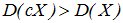 
. Если 0<½с½<1, то 
.
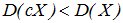Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:
[ m - 3s; m + 3s; ].(6.15)
49. Нормальное распределение непрерывной случайной величины: плотность вероятности и числовые характеристики.
Говорят, что с.в х распределена нормально с параметрами «а» и «σ», если ее плотность вероятности описывается функцией:
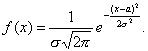
где а и σ —некоторые постоянные, называемые параметрами нормального распределения.
а- мат. ожидание
σ- среднее квадратическое отклонение
Функция распределения F(x) в рассматриваемом случае принимает вид
