Построение графика в Excel и использование функции ЛИНЕЙН

Рассмотрим результаты эксперимента, приведенные в исследованном выше примере.

Исследуем характер зависимости в три этапа:

- Построим график зависимости.

- Построим линию тренда (в данном случае это прямая ).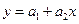

- Получим числовые характеристики коэффициентов этого уравнения.

Решение

Построение графика зависимости.

1. Выделим интервал А1:В25.

2. Вызовем Мастер диаграмм, нажав соответствующую кнопку на панели инструментов.

3. Используя мышь, выделим область для встроенной диаграммы.

4. На 1 шаге в диалоговом окне Мастера диаграмм интервал А1:В25 должен быть указан, если это не так укажите. Нажмите Шаг>.

5. На 2 шаге выберите тип диаграммы XY-точечная.Нажмите Шаг>.

6. На 3 шаге выберите первый тип автоформата. Нажмите Шаг>

7. На 4 шаге укажите следующие параметры:

8. Отвести 1 столбец для данных по оси Х; отвести 1 строку для текста легенды. Нажмите Шаг>.

9. На 5 шаге в окне «Название диаграммы: » введите заголовок «Линейная аппроксимация»; в окне «Категорий [X]:» введите «x»; в окне «Значений [Y]:» введите «y». Нажмите Закончить.

Построение линии тренда

Для построения линии тренда выполним следующую последовательность действий:

Дважды щелкнем по диаграмме. Диаграмма активизируется.

Щелкните по графику непосредственно в одну из изображенных точек. Сам график активизируется, его окраска изменится.

Вставляем линию тренда, воспользуемся меню Вставка – Линия тренда.

Появиться диалоговое окно «Линия тренда» выберем на вкладке «Тип» (Рис.2) линейный тип и перейдем к вкладке «Параметры».

На вкладке «Параметры» (Рис.3) потребуем показывать уравнение тренда на диаграмме и показывать значение , поставив их в соответствующие клетки. Нажмем кнопку ОК.

Рис.2

Рис.3

На диаграмме появится линия тренда с соответствующим уравнением. Также изменится легенда. При желании текстовое поле с уравнением и значением , а также название координат x и y, можно оттащить в более удобное место, как это сделано на Рис 4.

Рис.4

Для построения квадратичной аппроксимации на четвертом шаге в диалоговом окне «Линия тренда» выберем на вкладке «Тип» (Рис.2) полиномиальный тип степень 2. Результат представлен на рис.5.

Рис.5

Для построения экспоненциальной аппроксимации на четвертом шаге в диалоговом окне «Линия тренда» выберем на вкладке «Тип» (Рис.2) экспоненциальный тип. Результат представлен на рис.6.

Рис.6

Сравнивая результаты, полученные при помощи функции ЛИНЕЙН видим что они полностью совпадают с вычислениями, проведенными выше. Это указывает на то, что вычисления верны.

Примечание: Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает с истинным значением (это значение было сосчитано вручную выше) поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения 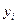, а преобразованные значения с дальнейшей линеаризацией.

Получение числовых характеристик зависимости

Для построения числовых характеристик необходимо создать табличную формулу, которая будет занимать 5 строк и 2 столбца. Этот интервал может располагаться в произвольном месте на рабочем листе. В этот интервал требуется ввести функцию ЛИНЕЙН. Для этого выполняем следующую последовательность действий:

- Выделите область A65:B69.

- Вызовите Мастер функций.

- Выберите функцию Линейн.

- Определим аргументы функции.

- В качестве изв_знач_уукажите В1:В25.

- В качестве изв_знач_хукажите А1:А25.

- Третье поле Константаоставьте пустым.

- В четвертом поле статнаберите истина.

- Нажмите кнопку Закончить.

- Установите курсор в строку формул.

- Нажмите комбинацию клавиш Ctrl+Shift+Enter, это обеспечит ввод табличной формулы!

В результате должны заполниться все ячейки интервала A65:B69(см. табл.9).

Таблица 9.

Поясним назначение некоторых величин, расположенных в табл.9.

Величины, расположенные в ячейках A67 и B67 характеризуют соответственно наклон и сдвиг.

A69 - коэффициент детерминированности.

A70 - F-наблюдаемое значение.

B68 - число степеней свободы.

A69 - регрессионная сумма квадратов.

B69 - остаточная сумма квадратов.

Рассмотрим назначение функции ЛИНЕЙН.

Эта функция использует метод наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Уравнение для прямой линии имеет следующий вид:

или ,

где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - это постоянная. Заметим, что y, x и m могут быть векторами.

Функция ЛИНЕЙН возвращает массив . ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

Синтаксис

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст; статистика)

Известные_значения_y - это множество значений y, которые уже известны для соотношения .

- Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x - это множество значений x, которые уже известны для соотношения .

- Массив известные_значения_x может содержать одно или несколько множеств переменных.

- Если используется только одна переменная, то известные_значения_y и известные_значения_x могут быть массивами любой формы при условии, что они имеют одинаковую размерность.

- Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).

Конст- это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

- Если констимеет значение ИСТИНА или опущена, то b вычисляется обычным образом.

- Если констимеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx .

Статистика- это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

- Если статистикаимеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид:

. (17)

- Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Дополнительная регрессионная статистика приведена в табл. 10

Таблица 10.

Величина	Описание
	Стандартные значения ошибок для коэффициентов .
	= #Н/Д, если конст имеет значение ЛОЖЬ.
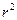	Коэффициент детерминированности.
	Стандартная ошибка для оценки y.
	F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет.
	Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.
	Регрессионная сумма квадратов.
	Остаточная сумма квадратов

В табл.11 показано, в каком порядке возвращается дополнительная регрессионная статистика.

Таблица 11.

		…
		…

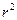Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная, тогда x, m и b вычисляются по следующим формулам:

, (18)

Эти формулы могут быть использованы для нахождения решения системы (4), вместо m и b следует подставить 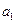и 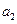.