Left Right Left Right

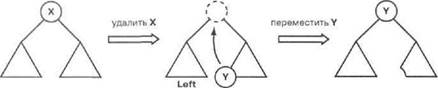
Рис, 9.7. Операция удаления элемента X из бинарного словаря, прикоторой возникает проблема, связанная с тем. что нужно восстано­вить структуру дерева после удаления X

ЕСЛИ ОДНО ИЗ поддеревьев (Left ИЛИ Right) является пустым, решение упрощает­ся: непустое поддерево должно быть присоединено к узлу А, А если оба поддерева непусты, то можно воспользоваться одной идеей, которая проиллюстрирована на рис, 9.8. Крайний левый узел поддерева Right (узел Y) переносится из его текущей позиции вверх для заполнения промежутка, образовавшегося в результате удаления узла X. После такого переноса дерево остается упорядоченным. Безусловно, та же идея допускает выполнение симметричной операции, предусматривающей перенос крайнего правого узла поддерева Left.

В соответствии с этими соображениями может быть составлена программа для операции удаления элемента из бинарного словаря, приведенная в листинге 9.5. Пе­ренос крайнего левого узла правого поддерева осуществляется с помощью следующе­го отношения: delminl Tree, Y, Treel)

где У - наименьший (т.е. крайний левый) узел дерева Tree, a Treel - дерево Tree после удаления элемента Y.

Глава 9, Операции со структурами данных

RfgM

Right

flight

rue. n.«. иперация заполнения промежутка, ооразовавшегося е результате уда­ления узла X

Листинг 9,5. Операция удаления из бинарного словаря

% del( Tree, X, NewTree):

% удаление элемента X ;'"-'. бинарного словаря Tree и получение словаря НеыТгее del( t( nil,X, Right), X, Right). dell t( Left, x, nil), X, Left).

del( t( Left, X, Right), X, t( Left, Y, Rightl)) :-

delmin( Right, Y, Rightl). del ( t( Left, Root, Right), X, t( Leftl, Root, Right)) Root, X) , del! Left, x, Leftl).

del ( t( Left, Root, Right), X, t( Left, Root, Rightl)) gt X, Root), del( Right, X, Rightl) ,

-

: -

% delminl Tree, ■, NewTree) :

удаление минимального элемента * и получение словаря NewTree

из бинарного словаря Tree

delraint t( nil,

R)

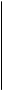
delmini t( Left, Root, Right), X, t( Leftl, Root, Right)) :-delmint Left, Y, Leftl).

Но для разработки операций добавления и удаления можно использовать другое изящное решение. Отношение add может быть определено недетерминированным способом, таким образом, чтобы вставка нового элемента выполнялась на любом уровне дерева, а не только на уровне листа. Ниже описаны правила выполнения та­кой операции вставки.

Чтобы ввести элемент X в бинарный словарь D, необходимо выполнить одно из следующих действий.

Ввести X в корень дерева D (так, чтобы X стал новым корнем).

Если корень D больше х, то вставить X в левое поддерево D, в противном случае вставить X в правое поддерево D.

Сложной частью этой операции является вставка элемента в корень дерева D. Сформулируем эту операцию как следующее отношение: addroot; D, X, D1)

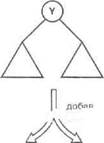
где X — элемент, который должен быть вставлен а корень D, a D1 — результирую­щий словарь, корнем которого является X. Зависимости между X, D и D1 показаны на

Часть I. Язык Prolog

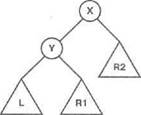
рис. 9.9. Остается найти ответ на вопрос о том. какими должны быть поддеревья Li и L2 на рис. 9.9 (или, при использовании другого варианта вставки, R1 и R2). Ответ на этот вопрос можно получить, рассмотрев следующие ограничения.

• L1 и L2 должны быть бинарными словарями.

• Множество узлов в и L2 равно множеству узлов в L.

• Все узлы в L1 меньше X и все узлы в I больше X.

._ итьХ /V в качестве кормр

Х<У

Ycx

D1

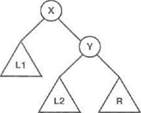
Рис. 9.9. Примеры вставки X в качестве корнябинарного словаря

ЭТИ ограничения налагаются только одним отношением — addrcot- А именно, если X должен быть введен в дерево L в качестве корня, то поддеревьями результи­рующего дерева как раз и должны быть L1 и L2. В языке Prolog L1 и L2 должны со­ответствовать следующей цели: addrootf L, X, t( Lb X, L2

Те же ограничения распространяются на - и R2: addroot! R_r X, tl Rl, X, R2))

В листинге 9.6 приведена полная программа с определением операции "недетер­минированной" вставки в бинарный словарь.

Листинг 9.6. Вставка в бинарный словарь на любом уровнедерева

i add( Tree, X, HewTree) : i вставка элемента X на любом уровне бинарного словаря Tree % и получение словаря КемТгее add[ Tree, X, HewTree) :- addroot; Tree, X, NewTree) . % Добавление элемента X в качестве нового корня

addf t( L, Y, R) , Y,, t ( LI, i, R) ) gt( Y, x), add( L, X, LI) .

add{ t ( L, Y, RJ , X, 1 ( L, Y, Rl)

:;■ X, Y) ,

% вставка элемента Х в левое поддерево Вставка элемента X в правое поддерево

Глава 9. Операции со структурами данных

add( К, X, Rl) .

4 addrootf Tree, X, HewTree):

Ч вставка элемента Х в качестве корня в дерево Tree и получение дерева HewTree

addrootf nil,X, t[ nil,X, nil)). % Вставка в пустое дерево

addroot ( tt L, Y, " , X, t( . X, t( L2, Y, R) ) ) :-

gt( Y, X), addroott L, X, t( 1, X, L2>>.

addroott t( L, Y, R), X, t( t( L, Y, Rl), X, R2)) :-

gt( X, Y),

addroott R, X, t( Rl, X, R2) ) .

Важной отличительной особенностью этой процедуры вставки является то, что она не налагает ограничений на выбор уровня вставки. Поэтому такую процедуру add можно применить в обратном направлении, для удаления любого элемента из сло­варя. Например, следующий список целей формирует словарь : . содержащий элементы 3, 5, 1, 6, а затем удаляет элемент 5, что приводит к получению словаря DD

add( nil,3, Di), add ( Dl, 5, D2) , add f D2, 1, D3) , add( D3, 6, D) , add f DD, 5, D)