Аналитический обзор литературы

Моделирование дифракционных характеристик голографических фотонных ФПМ-ЖК структур

Пояснительная записка

к курсовой работе по дисциплине «Информатика»

Студент гр. 153.

___________________ К.В. Волченко

“____” ______________ 2014г.

Руководитель

ассистент каф.СВЧиКР

____________________ А. О. Семкин

“____” ______________ 2014г.

Томск

Реферат

Курсовая работа 42с., 12 рис., 11источников.

Информатика, объектно-ориентированное программирование, С++, Qt, qwt, фотополимерно-жидкокристаллические материалы, ФПМ-ЖК, дифракция, дифракционные характеристики.

Объектом разработки является программа для моделирования дифракционных характеристик голографических фотонных ФПМ-ЖК структур.

Цель работы – разработка программного обеспечения для моделирования дифракционных характеристик голографических фотонных ФПМ-ЖК структур при воздействии на них пространственно неоднородного электрического поля, меняющего полярность в центре апертуры падающего светового пучка.

Реализована программа для моделирования дифракционных характеристик голографических фотонных ФПМ-ЖК структур.

Программное обеспечение разработано в среде QtCreator с использованием библиотеки qwt. Текстовые документы подготовлены в текстовом редакторе MicrosoftWord.

Министерство образования и науки Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И

РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧиКР)

УТВЕРЖДАЮ

Заведующий кафедрой СВЧиКР

___________ С.Н. Шарангович

“____” _____________ 2014г.

ЗАДАНИЕ

по курсовому проектированию по дисциплине

«Информатика»

студенту гр. 153 Волченко К.В.

1. Тема курсовой работы: Моделирование дифракционных характеристик голографических фотонных ФПМ-ЖК структур.

2. Срок сдачи работы на кафедру: - 5 июня 2014г.

3. Содержание работы и сроки выполнения этапов работы:

3.1. Изучение задания и рекомендованной литературы.

Изложение понятого в рабочей тетради. - первая неделя.

3.2. Разработка алгоритма хода программы и составление блок-схемы алгоритма, диаграммы классов - вторая неделя.

3.3. Написание программы на объектно-ориентированном языке - третья неделя.

3.4. Отладка программы на ЭВМ - четвертая и пятая неделя.

3.5. Анализ результатов, написание пояснительной записки на текстовом редакторе, всоответствии с требованиями к оформлению курсовых работ - седьмая и восьмая недели.

4. Рекомендованная литература:

4.1. С.Прата, Язык программирования C++. Лекции и упражнения. - М.: ДиаСофт. - 2002. – 896с.

4.2. Qt. Профессиональное программирование на C++ : Наиболее полное руководство / М. Шлее. - СПб.: БХВ-Петербург, 2005. - 544 с.

4.3. Семкин А.О., Шарангович С.Н. Взаимодействие световых пучков с голографическими фотонными ФПМ-ЖК-структурами при неоднородном управляющем электрическом поле // Известия вузов. Физика – 2013. – Т. 56, № 9/2 – С. 21-24.

Дополнительную литературу студент ищет самостоятельно в зависимости от темы исложности задания.

5. Исходные данные:

Программа должна обеспечивать расчет и визуализацию дифракционных характеристик, согласно теоретической модели, описанной в работе 4.3. В рамках курсовой работы должны быть реализованы:

5.1. Графический интерфейс программы.

5.2. Ввод исходных данных для расчета: параметров композиции (показатели преломления составляющих композиции, коэффициенты упругости жидкого кристалла, толщина образца) и параметров дифракции (объемная доля молекул ЖК в образце, вклад фракции ЖК в дифракционные процессы, длина волны считывающего светового излучения, угол Брэгга).

5.3. Построение графика изменения продольного профиля показателя преломления образца в зависимости от приложенного внешнего электрического поля.

6 Состав пояснительной записки:

6.1. Титульный лист.

6.2. Аннотация.

6.3. Лист задания с подписью преподавателя.

6.4. Содержание.

6.5. Введение. Постановка задачи.

6.6. Описание функционала моделирующей программы.

6.7. Описание алгоритма моделирования. Блок-схема алгоритма.

6.8. Расшифровка идентификаторов, диаграмма классов.

6.9. Исходный код программы, иллюстрации работы приложения.

6.10. Интерпретация результатов и выводы по проделанной работе.

6.11. Список используемой литературы.

7. Отчетность по работе:

7.1. В ходе выполнения работы - отчетность по фактическому материалу в

рабочей тетради ( в соответствии со сроками выполнения основных

этапов, указанных в п.3).

7.2. Пояснительная записка, в обязательном порядке со всеми разделами

по п.6. без исключения.

7.3 На электронном носителе - передается: файлы исходных кодов программы, пояснительная записка.

7.4. После оформления пояснительной записки - защита на кафедре.

Дата выдачи задания: 11февраля 2014г.

Подпись руководителя

ассистент каф. СВЧиКР_____________ А.О. Семкин

Задание принял к исполнению: 15 февраля 2014 г.

Студент гр.153 _____________ К.В. Волченко
Содержание

Введение. 7

1 Аналитический обзор литературы.. 8

1.1 Теоретическая модель. 8

1.2 Описание выбранных средств разработки. 11

2 Разработка алгоритма программы.. 15

2.1 Профиль показателя преломления по выражению.. 15

2.2 Интегральная фазовая расстройка. 16

2.3 Дифракционная характеристика. 17

2.4 Диаграмма классов. 18

3 Написание программы.. 19

3.1 Класс MainWindow.. 19

3.2 Вычислительный модуль для профиля показателя преломления. 19

3.3 Вычислительный модуль для интегральной фазовой расстройки. 19

3.4 Вычислительный модуль для передаточных функций. 19

4 Отладка программы на ЭВМ, сравнение полученных результатов. 21

Заключение. 24

Литература. 25

Приложение А. Описание класса MainWindow.. 26

Приложение Б. Листинг функций расчета профиля показателя преломления. 28

Приложение В. Листинг функций расчета интегральной фазовой расстройки. 32

Приложение Г. Листинг функций расчета дифракционных характеристик. 34

Приложение Д. Листинг программы в MathCAD.. 36

Введение

Создание управляемых оптических элементов коммутации и фильтрации на сегодняшний день является одним из наиболее актуальных направлений развития оптоволоконных систем связи. В качестве основы подобных устройств большой интерес представляют управляемые электрическим полем голографические фотонные структуры (ГФС), сформированные в композитном фотополимерном материале с жидкокристаллической компонентой (ФПМ-ЖК). В работах [9,10] получены аналитические модели взаимодействия световых пучков с ГФС в ФПМ-ЖК. Разработка программного обеспечения для моделирования характеристик ГФС по данным аналитическим моделям является необходимым условием для создания реальных устройств на их основе.

Целью данной курсовой работы является разработка программы позволяющей моделировать дифракционные характеристики голографических фотонных структур, сформированных в ФПМ-ЖК, при воздействии на них знакопеременного электрического поля.Требуется реализовать расчет и визуализацию дифракционных характеристик, в том числепостроение пространственного профиля показателя преломления образца ФПМ-ЖК, интегральной фазовой расстройки и дифракционной эффективности, в зависимости от введенных пользователем параметров материала, его толщины и величины воздействующего электрического поля.

Аналитический обзор литературы

Теоретическая модель

При разработке программы была использована теоретическая модель дифракции света на голографических фотонных ФПМ-ЖК-структурах, приведенная в [9,10]. Приведем здесь краткие математические выкладки из этой модели.

Рассмотрим двумерную дифракция Брэгга необыкновенных волн на голографической фотонной структуре (ГФС), сформированной в ФПМ-ЖК при воздействии внешнего пространственно неоднородного электрического поля (рисунок. 1).

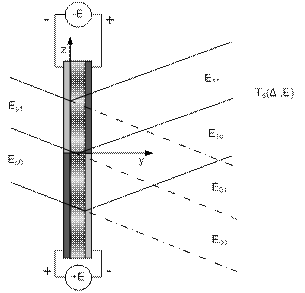Рисунок 1.1 – Схема дифракции световых пучков на ГФС в ФПМ-ЖК

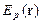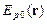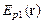Как видно из рисунка 1.1 на ГФС в ФПМ-ЖК воздействует знакопеременное электрическое поле, полученное путем формирования неоднородной топологии электродной структуры. Приняты следующие обозначения: – падающий пучок, здесь и далее для простоты анализа разделенный на два и , дифрагирующие на областях воздействия электрических полей разной полярности; соответствующие им 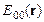и 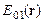– прошедшие 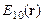и и 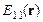– дифрагировавшие в первый порядок пучки; 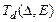– результирующая передаточная функция для пучка первого порядка дифракции, которая будет определена ниже; параметры 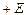и 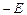обозначают поля противоположной полярности; 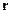– радиус-вектор.

Примем также, что изменение полярности управляющего напряжения приводит к повороту оси жидкого кристалла в противоположную сторону. Тогда локальные векторные диаграммы дифракции световых пучков будут иметь следующий вид (рисунок 2).

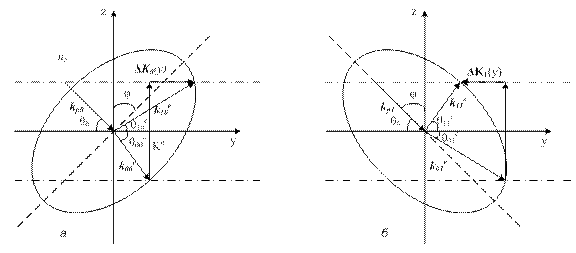
Рисунок 1.2 – Локальные векторные диаграммы дифракции необыкновенных волн при воздействии электрических полей противоположной полярности

На рисунке1.2 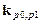– волновые векторы падающих пучков; 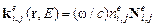– волновые векторы дифрагирующих пучков; i = 0,1 – порядок дифракции; j – номер пучка согласно рисунка 1.1; 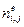– показатели преломления, 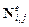–волновые нормали; e соответствует необыкновенной волне; 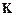–вектор решетки; 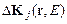– векторы локальной фазовой расстройки, φ – угол поворота оси директора ЖК.

Амплитуды взаимодействующих необыкновенных волн будем искать решением системы уравнений связанных волн (УСВ) [9,10]:

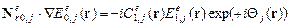, (1)

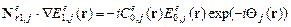, (2)

где 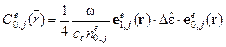– локальные коэффициенты связи; 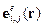– векторы поляризации; 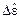– возмущение диэлектрической проницаемости образца, характеризующее периодическую неоднородность оптических свойств ГФС; 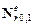– групповые нормали; 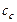– скорость света.

В уравнениях (1),(2) введен параметр интегральной фазовой расстройки для количественной оценки степени влияния пространственной неоднородности 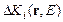на условия дифракции световых волн:

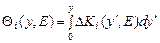, (3)

где 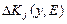– модуль пространственно-неоднородного вектора фазовой расстройки 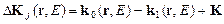, характеризующей изменение геометрии дифракции (рисунок 1.2) вследствие воздействия электрического поля. Величина 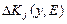определяется выражением:

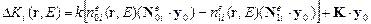. (4)

Входящие в (4) зависимости 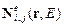находятся из уравнений эйконала. Согласно рисунка 1.2 показатели преломления 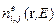для световых пучков, дифрагирующих на областях воздействия электрических полей разной полярности определяются:

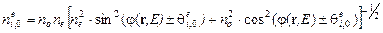, (5)

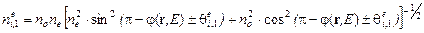, (6)

где 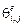– углы падения и дифракции необыкновенных волн (рис. 1.1), а зависимость 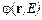определяется из уравнения Фредерикса [9,10]:

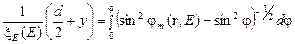, (7)

где 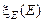– оптическая когерентная длина, d – толщина образца, 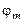– максимальный угол поворота директора ЖК.

Воспользуемся решением УСВ (1),(2) в оптически неоднородной среде в приближении заданного поля [9,10]. В этом случае распределение амплитуды дифракционного светового поля по угловому спектру (УС) можно представить в виде:

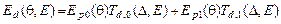, (8)

где введены парциальные передаточные функции (ПФ) ГФС:

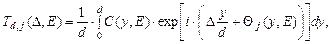(9)

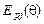– УС падающего светового поля; 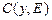– амплитудный коэффициент связи [9,10]; 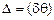– относительная фазовая расстройка, 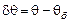– отклонение от угла Брэгга 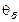, угол 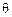характеризует направление плосковолновых компонент УС 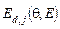относительно волновых нормалей 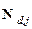световых пучков.

Полагая 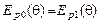, из (8) получим, что для анализа воздействия знакопеременного управляющего напряжения на дифракционные характеристики можно ввести результирующую ПФ (рисунок 1.1):

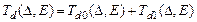. (10)

В данной работе разработке подлежит программный модуль, позволяющий последовательно численно рассчитать профили показателей преломления по выражениям (5), (6) при разных полярностях воздействующего электрического поля, параметр интегральной фазовой расстройки по выражению (3), парциальные (9) и суммарную (10) передаточные функции ГФС.

Следующий раздел будет посвящен разработке алгоритмов решения поставленных задач.