Теоретическое обоснование. 1. Программная реализация на языке С++ решения решения СЛАУ с помощью метода Гаусса - Зейделя

Цель работы

1. Программная реализация на языке С++ решения решения СЛАУ с помощью метода Гаусса - Зейделя.

2. Проверка работы составленной программы для заданной функции.

Система функции (1 вариант)

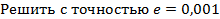
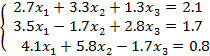
Теоретическое обоснование

Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.

Итерации по методу Зейделя отличаются от простых итераций тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1)-го приближения с меньшими номерами. При рассмотрении развернутой формы системы итерационный процесс записывается в виде (1):

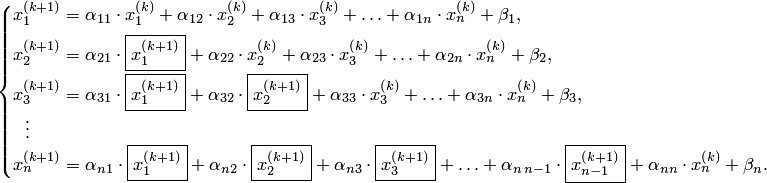
В каждое последующее уравнение подставляются значения неизвестных, полученных из предыдущих уравнений.

Теорема о достаточном условии сходимости метода Зейделя. Если для системы какая-либо норма матрицы меньше единицы, т.е. 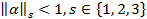, то процесс последовательных приближений (1) сходится к единственному решению исходной системы 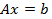при любом начальном приближении .

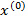Для обеспечения сходимости метода Зейделя требуется преобразовать систему 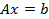к виду 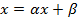с преобладанием диагональных элементов в матрице