Описание численного метода решения СЛАУ

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

«Автоматизация инженерных задач»

Выполнил: студент 1 курса заочного отделения инженерного факультета

Романцев Е.В.

Зачет. Книж №11776

Проверил: Зав.каф.

Чертова М.Н.

Великие Луки 2012г.

Содержание

1.Введение

2.Описание численного метода решения СЛАУ

2.1.Общяя характеристика методов

2.2. Метод Крамера в решении СЛАУ

3.Прикладное ПО применяемое для решения СЛАУ

4.Практическое применение MS Excel

4.1.Постановка задачи

4.2.Вычисление СЛАУ методом Крамера

4.2.1.Традиционный способ решения СЛАУ

4.2.2.Решение СЛАУ с помощью MS Excel

5.Заключение

6. Список литературы

1.Введение

Многие инженерные задачи требуют решения системы линейных алгебраических уравнений (СЛАУ). С появлением ВТ в математике активно развиваются направления связанные с реализацией методов решения таких задач с помощью ЭВМ, которые называют вычислительная математика. Для решения инженерных задач на ЭВМ с использованием численного метода чаще всего применяются готовые программы обеспечения, например: math cad, MS Excel и другие.

Целью косовой работы являются приобретение навыков автоматизации инженерных расчетов в табличном процессоре MS Excel.

Задачами курсовой работы являются:

1. Решить систему алгебраических уравнения методом Крамера традиционным способом.

2. Использовать MS Excel в решение системы алгебраических уравнений.

Описание численного метода решения СЛАУ

Линейные системы имеют в вычислениях очень большое зна­чение, так как к ним сводится приближенное решение широкого круга вычислительных задач вообще и экономических задач в ча­стности. Теория решения линейных систем достаточно хорошо разработана и во многих частях доведена до совершенства. Име­ется большое число разнообразных программных средств для ре­шения самых различных систем уравнений, в том числе плохо обусловленных, блочных, с разреженными матрицами и т.д. По­этому не будем здесь детально рассматривать все методы, а упо­мянем лишь основные идеи и их особенности.

2.1.Общяя характеристика методов

Методы решения линейных систем уравнений обычно разде­ляют на две большие группы. К первой группе относят методы, которые принято называть точными. Они позволяют для любых систем в принципе найти точные значения неизвестных после ко­нечного числа арифметических операций, каждая из которых вы­полняется точно.

Ко второй группе относят все методы, не являющиеся точны­ми. Их обычно называют приближенными итерационными, ре­шения в них получают в результате бесконечного процесса при­ближений. Особое место среди них (нередко их даже выделяют в отдельную группу) занимают вероятностные методы, в основу которых положены соображения, взятые из теории вероятностей. Такие методы полезны лишь в случаях очень высокой размерно­сти систем и здесь более упоминаться не будут.

В общем виде линейная система уравнений записывается сле­дующим образом:

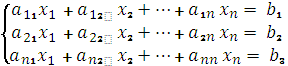
или чаще — в матричном виде: ах-В, где а — квадратная мат­рица размером n x n, B и x — векторы размером n (n — размер­ность системы).

ТОЧНЫЕ МЕТОДЫ

Точные методы обычно рассматриваются в курсах линейной алгебры, поэтому здесь упомянем коротко основные особенности самых распространенных методов для сопоставления с итераци­онными, которые обычно изучаются в курсах прикладной мате­матики.

Метод Гаусса сводится к двум этапам. На первом осущест­вляется приведение исходной системы уравнений с помощью преобразований к эквивалентной системе с верхней треугольной матрицей (т.е. приведение системы к треугольному виду). Преоб­разования сводятся к умножению всех членов уравнения на по­стоянное число, сложению уравнений, выражению отдельных пе­ременных через другие и т.п. Это прямой ход. На втором этапе, т.е. в обратном ходе (снизу вверх), находятся последовательно все переменные системы. В отдельных случаях, в частности при умножении всех членов уравнения на очень большое число (или при делении на очень маленькое), появляются большие вычисли­тельные ошибки, которые обусловливают значительные погреш­ности результатов решения.

Более практичным является метод оптимального исключе­ния, представляющий собой видоизменение метода Гаусса и требующий меньше памяти для решения. Здесь обратный ход соединен с прямым ходом за счет исключения всех уже выражен­ных переменных из вышестоящих уравнений.

Упомянем также метод Крамера (с использованием опреде­лителей), который требует очень больших вычислений уже при прямом решении систем из пяти—десяти уравнений, приведения матрицы А к форме произведения двух треугольных матриц, что позволяет свести решение заданной системы к последовательно­му решению двух систем с треугольными матрицами, что являет­ся задачей более простой. Поэтому вычисления определителей для матриц высокого порядка осуществляются обычно приближенными методами, и метод Крамера перестает быть в полном смысле точным.

Во всех методах этой группы может появляться накапливаю­щаяся вычислительная ошибка (не алгоритмическая!). Для ее контроля (а не для управления ею!) применяют специальные приемы. Например, в методе Гаусса к каждой строке добавляют еще один член, который равен сумме всех коэффициентов строки. С этим членом делают те же операции, что и с коэффициентами уравнения. На каждом шаге проверяют равенство суммы коэффи­циентов и “контрольного" добавленного члена: разница говорит о появлении накопившейся вычислительной погрешности. Можно оценивать не только абсолютную, но и относительную ошибку в равенстве суммы коэффициентов и “контрольного” добавленного члена. Таким образом, точные методы могут давать результат с погрешностью, которой трудно управлять и которая в ряде случа­ев может оказаться значительной, например при высоких поряд­ках системы.

В заключение отметим, что системы с плхо обусловленными матрицами коэффициентов нецелесообразно решать указанными методами вследствие возможности появления очень больших ошибок.

ПРИБЛИЖЕННЫЕ МЕТОДЫ

Эти методы дают возможность найти решение системы как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следую­щее, более точное приближение. Важной чертой таких методов является их самоисправляемость и простота реализации. Если в точных методах ошибка в вычислениях, когда она не компенси­руется случайно другими ошибками, неизбежно ведет к ошибкам в результате, то в случае сходящегося итерационного процесса ошибка в каком-то приближении исправляется в последующих вычислениях, и такое исправление требует только нескольких лишних шагов единообразных вычислений.

Условия и скорость сходимости каждого итерационного про­цесса существенно зависят от свойств уравнении, т.е. от свойств матрицы системы и от выбора начальных приближений.

ЗАПУСК ПРОГРАММЫ EXCEL

Запустить программу для создания, просмотра и работы в электронной таблице можно несколькими способами. Стандартным запуском можно считать следующие действия:

1. Щелкните на кнопке Пуск в левом нижнем углу панели задач.

2. Раскройте меню Программы.

3. В раскрывшемся меню выберите пункт Microsoft Excel.

Если пользователь часто обращается к Microsoft Excel, то он, обычно, выносит его в виде ярлыка на Рабочий стол. Тогда запуск, электронной таблицы на выполнение, сводится только к установке курсора на этот ярлык, щелкнув на нем левой клавишей мышки.

РАБОТА С ФОРМУЛАМИ

ОБЩИЕ ПОЛОЖЕНИЯ

Числовая обработка внесенных данных в электронную таблицу (ЭТ)¾ одна из главных задач Excel. ЭТ позволяет находить сумму рада чисел, производить вычитание, нахождение процента от общей суммы, строить различного вида графики и т.д.. Однако Excel позволяет производить вычисления по 320-ти функциям. Так, например, по названию товара, из прейскуранта, автоматически возвращается его стоимость и пересылается в указанную ячейку.

При создании, прежде всего, своих формул необходимо помнить ряд правил:

¨ Формулы начинаются со знака равенства (=).

¨ В формулу может входить до 1024-х символов (вряд ли Вам, когда либо, придется руководствоваться этим правилом, но надо помнить о нем !).

¨ Результат вычисления отображается в указанной ячейке, а формула, по которой производилось вычисление, в строке формул.

Как Вы уже успели заметить, необходимо при составлении формул знать фактически не три, а два правила. При необходимости внесения в формулу ссылки на некоторую ячейку легче и, главное, надежнее вводить ее имя не с клавиатуры (возможны ошибки !), а установить курсор мышки на необходимую ячейку и нажать левую клавишу мышки ¾ имя ячейки автоматически введется в формулу.

КОПИРОВАНИЕ ФОРМУЛ

Вы, наверное, при составлении формул уже убедились в том, что их составление достаточно трудоемкий процесс, даже при использовании мышки, при добавлении в нее ссылок на ячейки. А если таких формул, в процессе вычислений, потребуется несколько ? Затраты времени, на их создание, будут возрастать пропорционально их числу. Где же выход ? Копирование ¾ вот эффективный выход из создавшегося положения.

Для копирования формулы методом Автозаполнения можно использовать маркер заполнения (этот метод был описан в первой главе). При этом автоматически осуществляется последовательность создания, под вычисляемые строки (столбцы), формул. При копировании формул необходимо учитывать понятия относительных и абсолютных адресов ячеек. При необходимости копирования формулы в другую ячейку или группу ячеек (в этом случае Автозаполнение не годится), можно воспользоваться буфером обмена.

Относительные адреса ячеек появляются при копировании формул с автоматическим преобразованием ссылок на вычисление столбцов или строк таблицы. Так, например, в ячейке F7 записывается сумма строки «Покупка» (ячейки –В7 и С7), а при копировании этой формулы в ячейку F9, строка «Продажа», автоматически вычисляется сумма ячеек В9 и С9 с последующей записью результата в ячейку F9. То есть, имена ячеек В7 и С7, в написанной ранее формуле, автоматически заменились на В9 и С9

Но, иногда, необходимо зафиксировать один из адресов ячейки, тогда запись исходной формулы принимает вид, например:

=СУММ(А1:А4)*$А$5

Здесь, $А$5 – фиксированное имя ячейки, так, при переходе на колонку с именем В, формула автоматически преобразуется в:

=СУММ(В1:В4)*$А$5

При такой записи имени ячейки, с использованием знака «доллар» ($), называется ¾ абсолютным адресом ячейки.

Функция – это уже готовая сложная формула, по которой проводятся операции вычисления над группой данных определенного типа. Функции задаются с помощью формул, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке, называемом синтаксисом. Например, функция СУММ складывает значения или группы ячеек, а функция ППЛАТ вычисляет величину выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки. Функцию можно вводить в ячейку самостоятельно или при помощи Мастера функций.

МАСТЕР ФУНКЦИЙ

• Мастер функций позволяет использовать весь набор функций Excel, даже если вы точно не знаете их названия. Все функции организованы в группы (или категории), такие как Financial (Финансовые), Statistical (Статистические) и др. Мастер функций выводит краткое описание каждой функции, благодаря которому вы сможете выбрать нужную функцию. Кроме того, мастер функций помогает вводить аргументы функции и поясняет, для чего они нужны. При использовании мастера функций практически исключаются ошибки при записи формул в ячейки, кроме того, так удобнее вводить сложные функции с несколькими аргументами.

Для того, чтобы воспользоваться мастером функций необходимо:

1. Выделите ячейку, в которую нужно поместить функцию, и нажмите кнопку Вставка функции на стандартной панели инструментов.

2. В списке Категории функцийоткрывшегося окна диалога укажите нужную категорию функции.

3. Выберите нужную вам функцию в списке Имя функции. В нижней части окна диалога появится описание выбранной функции. Прочитайте его и убедитесь, что функция выбрана правильно. Щелкните на кнопке ОК.

4. Под строкой формул появится окно — так называемая палитра формул. Введите аргументы в соответствующие поля. Вы можете вводить значения или адреса ячеек вручную, а можете щелкать на нужных ячейках или выделять нужные диапазоны.

5. Щелкните на кнопке ОК, чтобы завершить ввод функции. Результат вычисления функции появится в ячейке.

ФАКТР(число)

Число - это неотрицательное число, факториал которого вычисляется. Если число не целое, то производится отбрасывание дробной части.

МОПРЕД - возвращает определитель матрицы (матрица хранится в массиве).

МОПРЕД(массив)

Массив - это числовой массив с равным количеством строк и столбцов.

Массив может быть задан как интервал ячеек, например, A1:C3 или как массив констант, например {1;2;3:4;5;6:7;8;9}.

КОРЕНЬ - возвращает положительное значение квадратного корня.

КОРЕНЬ(число)

Число - это число, для которого вычисляется квадратный корень. Если число отрицательно, то функция КОРЕНЬ возвращает значение ошибки #ЧИСЛО!.

ABS - возвращает модуль (абсолютную величину) числа. Абсолютная величина числа - это число без знака.

ABS(число)

Число - это действительное число, абсолютную величину которого требуется найти.

ПИ - возвращает число 3,14159265358979, математическую константу p с точностью до 15 цифр.

ПИ( )

Логические функции

Логические функции предназначены для проверки выполнения условия или для проверки нескольких условий. Так, функция ЕСЛИ позволяет определить, выполняется ли указанное условие, и возвращает одно значение если условие истинно, и другое — если оно ложно.

Синтаксис функции:

ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь)

Например: ЕСЛИ (А1>15; a1*15; 0), что означает:

Если условие А1>15 выполняется, то содержимое ячейки, в которую помещена функция, вычисляется по формуле A1*15. Если это условие не выполняется, то содержимое ячейки = 0.

В следующем примере, если значение ячейки A10 = 100, то лог_выражение имеет значение ИСТИНА и вычисляется сумма для ячеек B5:B15. В противном случае лог_выражение имеет значение ЛОЖЬ и возвращается пустой текст (""), очищающий ячейку, которая содержит функцию ЕСЛИ

ЕСЛИ(A10=100;СУММ(B5:B15);" ")

Также часто используются следующие логические функции:

¨ Функция Ивозвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ.

¨ Функция ИЛИвозвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ.

¨

Функции работы с датой и временем

Функции работы с датой и временем позволяют анализировать и работать со значениями даты и времени в формулах. Например, если требуется использовать в формуле текущую дату, воспользуйтесь функцией СЕГОДНЯ, возвращающей текущую дату по системных часов.

Инженерные функции

Инженерные функции служат для выполнения инженерного анализа. Инженерные функции можно разделить на три группы:

· функции для работы с комплексными переменными;

· функции для преобразования чисел из одной системы счисления в другую (десятичную, шестнадцатеричную, восьмеричную и двоичную);

· функции для преобразования величин из одной системы мер и весов в другую.

Функции обработки текста

С помощью функций обработки текста можно с помощью формул производить действия над строкам текста — например, изменить регистр или определить длину строки. Можно также объединить несколько строк в одну.

Информационные функции

Информационные функции предназначены для определения типа данных, хранимых в ячейке. Информационные функции проверяют выполнение какого-то условия и возвращают в зависимости от результата значение ИСТИНА или ЛОЖЬ. Так, если ячейка содержит четное значение, функция ЕЧЁТН возвращает значение ИСТИНА. Если в диапазоне функций имеется пустая ячейка, можно воспользоваться функцией СЧИТАТЬПУСТОТЫ, либо ЕПУСТО.

Статистические функции

Статистические функции позволяют выполнять статистический анализ диапазонов данных. Например, с помощью статистической функции можно провести прямую по группе значений, вычислить угол наклона и точку пересечения с осью Y и прочее.

Финансовые функции

С помощью финансовых функций осуществляются такие типичные финансовые расчеты, как вычисление суммы платежа по ссуде, объем периодической выплаты по вложению или ссуде, стоимость вложения или ссуды по завершении всех отложенных платежей.

Аргументами финансовых функций часто являются следующие величины:

· будущее значение – стоимость вложения или ссуды по завершении всех отложенных платежей;

· количество выплат – общее количество платежей или периодов выплат;

· выплата – объем периодической выплаты по вложению или ссуде;

· текущее значение – начальная стоимость вложения или ссуды. Так, начальная стоимость ссуды равна, собственно, сумме займа;

· ставка – процентная ставка или скидка по вложению или ссуде;

· режим выплат – режим выплат, с которым осуществляются выплаты (в конце или в начале месяца).

Функции работы с базами данных

Если необходимо убедиться в том, что значения списка удовлетворяют условию, можно использовать функции работы с базами данных. С их помощью, например, можно определить количество записей в таблице о продажах или извлечь те записи, в которых значение поля «Сумма» больше 1000 но меньше 2500.

Функции ссылки и автоподстановки

Если необходимо осуществлять поиск в списках или таблицах или если необходимо найти ссылку к ячейке, можно воспользоваться функциями ссылки и автоподстановки. Например, для поиска значения в таблице можно использовать функцию ВПР

Заключение.

СПИСОК ЛИТЕРАТУРЫ

1. А. В. Голышева, В. Н. Корнеев. Excel 2007 без воды. 2008 г.

2. Ю. В. Васильков, Н. М. Василькова. Компьютерные технологии вычислений. 2002 г.

3. В. В. Трофимова. Информатика. 2011 г.

4. Н. А. Лизунова, С. П. Шкроба. Матрицы и системы линейных уравнений. 2007 г.

5. Е. А. Веденеева. Функции и формулы Excel 2007. 2008 г.

6. А. Г. Днепров. Excel 2007 видеосамоучитель. 2008 г.

7. И. Киреев, А. В. Пантелеев. Численные методы в примерах и задачах.

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

«Автоматизация инженерных задач»

Выполнил: студент 1 курса заочного отделения инженерного факультета

Романцев Е.В.

Зачет. Книж №11776

Проверил: Зав.каф.

Чертова М.Н.

Великие Луки 2012г.

Содержание

1.Введение

2.Описание численного метода решения СЛАУ

2.1.Общяя характеристика методов

2.2. Метод Крамера в решении СЛАУ

3.Прикладное ПО применяемое для решения СЛАУ

4.Практическое применение MS Excel

4.1.Постановка задачи

4.2.Вычисление СЛАУ методом Крамера

4.2.1.Традиционный способ решения СЛАУ

4.2.2.Решение СЛАУ с помощью MS Excel

5.Заключение

6. Список литературы

1.Введение

Многие инженерные задачи требуют решения системы линейных алгебраических уравнений (СЛАУ). С появлением ВТ в математике активно развиваются направления связанные с реализацией методов решения таких задач с помощью ЭВМ, которые называют вычислительная математика. Для решения инженерных задач на ЭВМ с использованием численного метода чаще всего применяются готовые программы обеспечения, например: math cad, MS Excel и другие.

Целью косовой работы являются приобретение навыков автоматизации инженерных расчетов в табличном процессоре MS Excel.

Задачами курсовой работы являются:

1. Решить систему алгебраических уравнения методом Крамера традиционным способом.

2. Использовать MS Excel в решение системы алгебраических уравнений.

Описание численного метода решения СЛАУ

Линейные системы имеют в вычислениях очень большое зна­чение, так как к ним сводится приближенное решение широкого круга вычислительных задач вообще и экономических задач в ча­стности. Теория решения линейных систем достаточно хорошо разработана и во многих частях доведена до совершенства. Име­ется большое число разнообразных программных средств для ре­шения самых различных систем уравнений, в том числе плохо обусловленных, блочных, с разреженными матрицами и т.д. По­этому не будем здесь детально рассматривать все методы, а упо­мянем лишь основные идеи и их особенности.

2.1.Общяя характеристика методов

Методы решения линейных систем уравнений обычно разде­ляют на две большие группы. К первой группе относят методы, которые принято называть точными. Они позволяют для любых систем в принципе найти точные значения неизвестных после ко­нечного числа арифметических операций, каждая из которых вы­полняется точно.

Ко второй группе относят все методы, не являющиеся точны­ми. Их обычно называют приближенными итерационными, ре­шения в них получают в результате бесконечного процесса при­ближений. Особое место среди них (нередко их даже выделяют в отдельную группу) занимают вероятностные методы, в основу которых положены соображения, взятые из теории вероятностей. Такие методы полезны лишь в случаях очень высокой размерно­сти систем и здесь более упоминаться не будут.

В общем виде линейная система уравнений записывается сле­дующим образом:

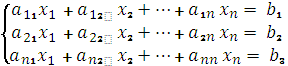
или чаще — в матричном виде: ах-В, где а — квадратная мат­рица размером n x n, B и x — векторы размером n (n — размер­ность системы).

ТОЧНЫЕ МЕТОДЫ

Точные методы обычно рассматриваются в курсах линейной алгебры, поэтому здесь упомянем коротко основные особенности самых распространенных методов для сопоставления с итераци­онными, которые обычно изучаются в курсах прикладной мате­матики.

Метод Гаусса сводится к двум этапам. На первом осущест­вляется приведение исходной системы уравнений с помощью преобразований к эквивалентной системе с верхней треугольной матрицей (т.е. приведение системы к треугольному виду). Преоб­разования сводятся к умножению всех членов уравнения на по­стоянное число, сложению уравнений, выражению отдельных пе­ременных через другие и т.п. Это прямой ход. На втором этапе, т.е. в обратном ходе (снизу вверх), находятся последовательно все переменные системы. В отдельных случаях, в частности при умножении всех членов уравнения на очень большое число (или при делении на очень маленькое), появляются большие вычисли­тельные ошибки, которые обусловливают значительные погреш­ности результатов решения.

Более практичным является метод оптимального исключе­ния, представляющий собой видоизменение метода Гаусса и требующий меньше памяти для решения. Здесь обратный ход соединен с прямым ходом за счет исключения всех уже выражен­ных переменных из вышестоящих уравнений.

Упомянем также метод Крамера (с использованием опреде­лителей), который требует очень больших вычислений уже при прямом решении систем из пяти—десяти уравнений, приведения матрицы А к форме произведения двух треугольных матриц, что позволяет свести решение заданной системы к последовательно­му решению двух систем с треугольными матрицами, что являет­ся задачей более простой. Поэтому вычисления определителей для матриц высокого порядка осуществляются обычно приближенными методами, и метод Крамера перестает быть в полном смысле точным.

Во всех методах этой группы может появляться накапливаю­щаяся вычислительная ошибка (не алгоритмическая!). Для ее контроля (а не для управления ею!) применяют специальные приемы. Например, в методе Гаусса к каждой строке добавляют еще один член, который равен сумме всех коэффициентов строки. С этим членом делают те же операции, что и с коэффициентами уравнения. На каждом шаге проверяют равенство суммы коэффи­циентов и “контрольного" добавленного члена: разница говорит о появлении накопившейся вычислительной погрешности. Можно оценивать не только абсолютную, но и относительную ошибку в равенстве суммы коэффициентов и “контрольного” добавленного члена. Таким образом, точные методы могут давать результат с погрешностью, которой трудно управлять и которая в ряде случа­ев может оказаться значительной, например при высоких поряд­ках системы.

В заключение отметим, что системы с плхо обусловленными матрицами коэффициентов нецелесообразно решать указанными методами вследствие возможности появления очень больших ошибок.

ПРИБЛИЖЕННЫЕ МЕТОДЫ

Эти методы дают возможность найти решение системы как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следую­щее, более точное приближение. Важной чертой таких методов является их самоисправляемость и простота реализации. Если в точных методах ошибка в вычислениях, когда она не компенси­руется случайно другими ошибками, неизбежно ведет к ошибкам в результате, то в случае сходящегося итерационного процесса ошибка в каком-то приближении исправляется в последующих вычислениях, и такое исправление требует только нескольких лишних шагов единообразных вычислений.

Условия и скорость сходимости каждого итерационного про­цесса существенно зависят от свойств уравнении, т.е. от свойств матрицы системы и от выбора начальных приближений.