Задания для самостоятельной работы
1. Ветвление в вычислительных алгоритмах
Вариант 1.
1. Написать программу, которая по паролю будет определять уровень доступа сотрудника к секретной информации в базе данных. Доступ к базе имеют только шесть человек, разбитых на три группы по степени доступа. Они имеют следующие пароли: 9583, 1747 — доступны модули баз А, В, С; 3331, 7922 — доступны модули баз В, С; 9455, 8997 — доступен модуль базы С.
2. Пользователь вводит с клавиатуры три целых числа a,b,c. Необходимо вывести на экран наибольшее из этих чисел.
Вариант 2
1. Вычислить значение функции:
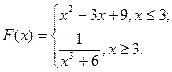
2. Дано трехзначное число. Написать программу, определяющую кратна ли шести сумма его цифр.
Вариант 3
1. В ЭВМ поступают результаты соревнований по плаванию для трех спортсменов. Составить программу, которая выбирает лучший результат и выводит его на экран с сообщением, что это результат победителя заплыва.
2. Пользователь вводит с клавиатуры три целых числа a,b,c. Необходимо вывести на экран наибольшее из этих чисел.
Вариант 4
1. Даны три положительных числа. Определить, можно ли построить треугольник со сторонами, длины которых равны этим числам. Если возможно, то ответить на вопрос, является ли он прямоугольным.
2. Напишите программу, запрашивающую три вещественных числа и выводящую их на экран в упорядоченном по возрастанию виде.
Вариант 5.
1. Составьте программу, которая уменьшает первое число в пять раз, если оно больше второго по абсолютной величине.
2. Даны три числа a, b, c. Определить, какое из них равно d. Если ни одно не равно d, то найти max (d-a, d-b, d-c).
Вариант 6.
1. Вычислить значение функции:
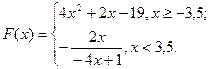
2. Дано четырехзначное число. Написать программу определения больше ли цифра сотен цифры единиц.
Вариант 7
1. Определить, является ли номер автобусного билета счастливым числом. Номер задается шестизначным числом.
2. Даны три вещественных числа a,b,c. Напишите программу, определяющую, могут ли данные числа являться длинами сторон равностороннего треугольника.
Вариант 8.
1. Даны три вещественных числа a,b,c. Напишите программу, определяющую, могут ли данные числа являться длинами сторон любого треугольника.
2. Дана точка с координатами (x,y), требуется определить принадлежность точки отрезку (a,b).
Вариант 9.
1. Даны три вещественных числа a,b,c. Напишите программу, определяющую, могут ли данные числа являться длинами сторон прямоугольного треугольника.
2. В точке (x0,y0) находится центр круга радиусом R. Напишите программу, определяющую, находится ли точка с заданными координатами (x,y) внутри или за пределами круга.
Вариант 10.
1. Дана точка с координатами (x,y), определите, принадлежит ли точка осям координат.
2. Напишите программу, запрашивающую три вещественных числа и выводящую их на экран в упорядоченном по убыванию виде.
2. Циклические алгоритмы
Все задачи требуется решить, используя цикл с параметром.
Вариант 1.
1. Найти сумму всех n-значных чисел (1 < n < 4).
2. Даны два целых числа A и B (A < B). Найти сумму всех целых чисел от A до B включительно.
Вариант 2.
1. Дано действительное число а, натуральное число n. Вычислить:
P = a(a – n)(a – 2n) x … x (a – n2).
2. Даны два целых числа A и B (A < B). Найти произведение всех целых чисел от A до B включительно.
Вариант 3.
1. Дано натуральное число n. Вычислить:
S = 1! + 2! + 3! + … + n! (n>1).
2. Даны два целых числа A и B (A < B). Найти сумму квадратов всех целых чисел от A до B включительно.
Вариант 4.
1. Дано натуральное число n. Вычислить:
S = 1/32 + 1/52 + 1/72 + … + 1/(2n + 1)2.
2. Даны два целых числа A и B (A < B). Найти частное, получаемое при делении А на все делители из диапазона целых чисел от A до B включительно.
Вариант 5.
1. Написать программу, которая вычисляет сумму n- первых членов ряда 1+1/2+1/3+1/4+… Количество суммируемых членов ряда задается во время работы программы.
2. Дано целое число N (> 0). Найти произведение
N! = 1·2·…·N
Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и вывести его как вещественное число.
Вариант 6.
1. Написать программу, которая вводит с клавиатуры последовательность из пяти дробных чисел и после ввода каждого числа выводит среднее арифметическое полученной части последовательности.
2. Дано целое число N (> 0). Найти сумму
N2 + (N + 1)2 + (N + 2)2 + … + (2·N)2
Вариант 7.
1. Написать программу, которая генерирует три последовательности из десяти случайных чисел в диапазоне от 1 до 10, выводит каждую последовательность на экран и вычисляет среднее арифметическое каждой последовательности.
2. Дано целое число N (> 0). Найти сумму
1 + 1/2 + 1/3 + … + 1/N
Вариант 8.
1. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в десятичной системе счисления.
2. Дано вещественное число — цена 1 кг яблок. Вывести стоимость 1.2, 1.4, …, 2 кг конфет.
Вариант 9.
1. Даны целые числа K и N (N > 0). Вывести N раз число K.
2. Выполнить табулирование функции y = cos(x + a) на отрезке [1, 10] c шагом h=1.
Варbант 10.
1. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 1, 2, …, 10 кг конфет.
2. Вычислить сумму значений функции у = x2 на отрезке [1, 5] c шагом 1.
Составить алгоритмы для следующих задач, используя циклы с предусловием и постусловием.
Вариант 1.
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?
2. Определить, какие различные цифры входят в заданное целое число.
Вариант 2.
1. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько амеб будет 3, 6, 9, 12, …, 24 часа.
2. Вывести все квадраты натуральных чисел, не превосходящие данного числа N.
Вариант 3.
1. Написать программу, вычисляющую сумму и среднее арифметическое последовательности положительных чисел, которые вводятся с клавиатуры.
2. Вычислить НОД двух чисел А и В.
Вариант 4.
1. Написать программу, которая определяет максимальное число из введенной с клавиатуры последовательности положительных чисел (длина последовательности не ограничена).
2. Дано число. Найти сумму и произведение его цифр.
Вариант 5.
1. Написать программу, которая проверяет, является ли целое число, введенное пользователем, простым.
2. Написать программу для решения следующей задачи: рост ребенка на начало года – 120 см. За месяц он подрастает на 2%. Через сколько месяцев его рост станет больше или равным 150 см.?
Вариант 6.
1. Составьте программу для нахождения всех автоморфных чисел в отрезке [m,n]. Автоморфным называется целое число, которое равно последним числам своего квадрата. Например: 52=25, 62=36, 252=625.
2. Начальный вклад в банке равен 1000 руб. Через каждый месяц размер вклада увеличивается на P процентов от имеющейся суммы (P — вещественное число, 0 < P < 25). По данному P определить, через сколько месяцев размер вклада превысит 1100 руб., и вывести найденное количество месяцев K (целое число) и итоговый размер вклада S (вещественное число).
Вариант 7.
1. Написать программу, которая вычисляет НОК двух целых чисел.
2. Дано целое число N (> 0). Используя операции деления нацело и взятия остатка от деления, вывести все его цифры, начиная с самой правой (разряда единиц).
Вариант 8.
1. Написать программу, вычисляющую произведение положительных четных чисел до 10.
2. Дано целое число N (> 0). С помощью операций деления нацело и взятия остатка от деления определить, имеется ли в записи числа N цифра «2». Если имеется, то вывести True, если нет — вывести False.
Вариант 9.
1. Написать программу, вычисляющую значение выражения y= 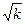 для k=1,3,5,7,9.
для k=1,3,5,7,9.
2. Дано целое число N (> 0). С помощью операций деления нацело и взятия остатка от деления определить, имеются ли в записи числа N нечетные цифры. Если имеются, то вывести True, если нет — вывести False.
Вариант 10.
1. Натуральные числа а, b, с называются числами Пифагора, если выполняется условие а2 + b2 = с2. Напечатать все числа Пифагора меньшие N.
2. Дано n вещественных чисел. Найти их среднее арифметическое.
3. Машина Поста
Вариант 1. На ленте имеется некоторое множество меток (общее количество меток не менее 1). Между метками множества могут быть пропуски, длина которых составляет одну ячейку. Заполнить все пропуски метками.
Вариант 2. На ленте имеется массив из n отмеченных ячеек. Каретка обозревает крайнюю левую метку. Справа от данного массива на расстоянии в m ячеек находится еще одна метка. Составьте для машины Поста программу, придвигающую данный массив к данной ячейке.
Вариант 3. Известно, что на ленте машины Поста находится метка. Напишите программу, которая находит ее.
Вариант 4. Дан массив меток. Каретка располагается где-то над массивом, но не над крайними метками. Стереть все метки, кроме крайних, и поставить каретку в исходное положение.
Вариант 5. На ленте машины Поста расположено n массивов меток, отделенных друг от друга свободной ячейкой. Каретка находится над крайней левой меткой первого массива. Определить количество массивов.
Вариант 6. На ленте расположены два массива разной длины. Каретка обозревает крайний элемент одного из них. Составьте программу для машины Поста, сравнивающую длины массивов и стирающую больший из них. Отдельно продумайте случай, когда длины массивов равны.
Вариант 7. На ленте машины Поста находятся два массива в m и n меток. Составить программу выяснения, одинаковы ли массивы по длине.
Вариант 8. Дано N массивов меток. Массивы разделены тремя пустыми ячейками. Количество меток в массиве не меньше двух. Если количество меток в массиве кратно трем, то стереть метки в этом массиве через одну, в противном случае стереть весь массив. Каретка находится над крайней левой меткой первого массива.
Вариант 9. На ленте машины Поста расположен массив из n меток. Составить программу, действуя по которой машина выяснит, делится ли число n на 3. Если да, то после массива через одну пустую ячейку поставить метку.
Вариант 10. Дано несколько массивов меток. Удалить четные массивы. Каретка находится над первым массивом.
4. Машина Тьюринга
Вариант 1. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 2. Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1. Автомат в состоянии q1 обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 3. Дана десятичная запись натурального числа n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии q1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 4. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 5. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “( )”. Например, дано “) ( ( ) ( ( )”, надо получить “) . . . ( ( ”. Автомат в состоянии q1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 6. Дана строка из букв “a” и “b”. Разработать машину Тьюринга, которая переместит все буквы “a” в левую, а буквы “b” — в правую части строки. Автомат в состоянии q1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 7. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2. Автомат в состоянии q1 обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 8. Даны два натуральных числа m и n, представленные в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q1обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 9. Даны два натуральных числа m и n, представленных в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n. Известно, что m > n. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Вариант 10. На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово “да”, иначе — “нет”. Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
5. Вспомогательные алгоритмы. Процедуры и функции.
Вариант 1. В квадратной матрице размером 5х5, заполненной случайными целыми числами из диапазона (–45,+45) найти количество положительных элементов.
Вариант 2. В квадратной матрице размером 5х5, заполненной случайными целыми числами из диапазона (–40,+40) найти соответственно максимальный отрицательный и минимальный положительный элементы.
Вариант 3. Описать процедуру Minmax(X, Y), записывающую в переменную X минимальное из значений X и Y, а в переменную Y — максимальное из этих значений (X и Y — вещественные параметры, являющиеся одновременно входными и выходными). Используя четыре вызова этой процедуры, найти минимальное и максимальное из данных чисел A, B, C, D.
Вариант 4. Даны три квадратных матрицы А, В, С n-го порядка. Вывести на печать ту из них, норма которой наименьшая. Пояснение. Нормой матрицы назовем максимум из абсолютных величин ее элементов.
Вариант 5. Пусть даны две вещественные матрицы порядка n. Получите новую матрицу прибавлением к элементам каждого столбца первой матрицы, произведения элементов соответствующих строк второй матрицы.
Вариант 6. Пусть даны две вещественные матрицы порядка n. Получите новую матрицу умножением минимального элемента каждой строки первой матрицы на наибольший элемент соответствующего столбца второй матрицы.
Вариант 7. Описать процедуру Mean(X, Y, AMean, GMean), вычисляющую среднее арифметическое AMean = (X + Y)/2 и среднее геометрическое GMean = sqrt(XY) двух положительных чисел X и Y (X и Y — входные, AMean и GMean — выходные параметры вещественного типа). С помощью этой процедуры найти среднее арифметическое и среднее геометрическое для пар (A, B), (A, C), (A, D), если даны A, B, C, D.
Вариант 8. Описать процедуру TrianglePS (a, P, S), вычисляющую по стороне a равностороннего треугольника его периметр P и площадь S. (a — входной, P и S — выходные параметры; все параметры являются вещественными). С помощью этой процедуры найти периметры и площади трех равносторонних треугольников с данными сторонами.
Вариант 9. Описать процедуру DigitCountSum(K, C, S), находящую количество C цифр целого положительного числа K, а также их сумму S (K — входной, C и S — выходные параметры целого типа). С помощью этой процедуры найти количество и сумму цифр для каждого из пяти данных целых чисел.
Вариант 10. Описать процедуру Swap(X, Y), меняющую содержимое переменных X и Y (X и Y — вещественные параметры, являющиеся одновременно входными и выходными). С ее помощью для данных переменных A, B, C, D последовательно поменять содержимое следующих пар: A и B, C и D, B и C и вывести новые значения A, B, C, D.
