Математическая формулировка

Порядок выполнения работы

1. Ознакомиться с методическими указаниями.

2. Получить у преподавателя постановку задачи.

3. Осуществить полную предмашинную подготовку задачи.

4. Выполнить машинную обработку полученных программ.

5. Проанализировать полученные результаты.

6. Оформить техническую документацию (отчёт).

7. Защитить работу.

Предмашинная подготовка задачи

К классу циклических процессов с табличным заданием (изменением) аргумента относятся вычислительные процессы вида

y_i = f(x_i)

при задании аргумента конкретными численными значениями

x₁, x₂, . . . , x_i, . . . , x_m.

В математике такая последовательность переменных называется одномерным массивом.

Массив – упорядоченная совокупность однородных элементов (данных), имеющих одно имя и разные индексы.

Каждый массив (матрица) характеризуется тремя параметрами:

· именем;

· размерностью (количеством измерений);

· размером.

Имя – основная часть обозначения массива (каждого его элемента). В качестве имени массива в математике, как правило, используются заглавные буквы, например: A, X, B. Элементы массива обозначают строчными буквами с индексами, например: a₁, x_k, b_{i j}, y_{k 8}, z_{k p t}.

Размерность – число измерений (направлений изменения) массива. Размерность определяет количество индексов у каждого элемента массива.

Одномерный массив имеет одно направление изменения, а каждый элемент – один индекс. Если измерений больше одного, массив относится к многомерным. Большинство из многомерных массивов – двумерные и трёхмерные.

Двумерный массив можно представить в виде таблицы (матрицы), при этом первое измерение определяет строку, второе – столбец. Каждый элемент двумерного массива имеет два индекса. Первый задает номер строки, второй – номер столбца элемента в таблице.

Трехмерный массив – последовательная совокупность одинаковых по структуре таблиц (страниц). Следовательно, каждый элемент такого массива имеет три индекса, первый из которых определяет номер страницы, второй – номер строки, третий – номер столбца, где расположен элемент.

В качестве индексов элементов могут использоваться числа, переменные и арифметические выражения целого типа, например: 8, i, j+2. Поэтому обозначения элементов одномерного массива X – x₁, x_j, x_j+2; двумерного Y – y_{2 6}, y_{i j}, y_{k j+3}; трехмерного Z – z _{2 6 4}, z _{i j k}, z _{i j+6 k-4}.

Размер – величина, определяющая максимальное количество элементов массива.

В математике размер записывается в круглых скобках после имени массива и указывается отдельно по каждому измерению. Для многомерных (двумерных и трехмерных) массивов последовательность указания размеров аналогична рассмотренной для индексов. Для указания размера могут использоваться числа и переменные целого типа.

Например, обозначения Y(7), X(m) определяют одномерные массивы Y и X размером 7 и m элементов соответственно. Двумерный массив D, состоящий из 20 строк и 30 столбцов, обозначается как D(20×30). Его размер определяет число элементов (20×30=600) в массиве. Двумерный массив Z из m строк и n столбцов обозначается как Z(m×n), а его размер вычисляют как произведение указанных величин. Трехмерный массив S из десяти страниц с пятью строками и пятнадцатью столбцами на каждой обозначается как S(10×5×15), т.е. состоит из 10×5×15=750 элементов.

Следовательно, в рассматриваемой задаче вычисления y_i = f(x_i) табличное задание аргумента соответствует одномерному массиву X(m) с именем X и размером m, текущий элемент которого обозначается x_i.

Постановка задачи

Рассчитать размер вознаграждений, получаемых сдатчиками кладов, если известно, что он составляет 25 % оценочной стоимости, при условии, что количество кладов равно 7, а оценочные стоимости составляют 492 тыс. р., 503, 948, 738, 892, 320, 250 тыс. р.

Математическая формулировка

Анализ постановки задачи позволяет сделать вывод, что оценочные стоимости кладов можно представить в виде одномерного массива с именем, например C, размерностью 1 и размером 7, т.е. массива C(7). При этом каждый элемент массива будет обозначаться как ci при изменении индекса i от 1 до 7.

Исходные данные

c1 = 492 тыс. р.	– стоимость 1-го клада;
c2 = 503 тыс. р.	– стоимость 2-го клада;
c3 = 948 тыс. р.	– стоимость 3-го клада;
c4 = 738 тыс. р.	– стоимость 4-го клада;
c5 = 892 тыс. р.	– стоимость 5-го клада;
c6 = 320 тыс. р.	– стоимость 6-го клада;
c7 = 250 тыс. р.	– стоимость 7-го клада;
про = 25 %	– процент вознаграждения.

1.2.2 Расчётные зависимости

пi = ci про/100	[тыс.р.= тыс.р. % / %]	– выплачиваемая премия;
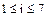		– диапазон изменения индекса;
i=i+1		– закон изменения индекса.

Выбор метода решения

Анализ полученной математической формулировки позволяет сделать выводы:

· необходим многократный расчет выплачиваемой премии пi как функции от стоимости каждого клада c_i (элемента массива C);

· найти закономерность между численными значениями элементов c_i не представляется возможным. Однако анализ их обозначений позволяет в качестве параметра цикла использовать индекс i, который изменяется от элемента к элементу по закону i=i+1 в диапазоне от 1 до 7;

· диапазон изменения параметра цикла i позволяет сформировать его начальное значение i=1 и условие повторения цикла 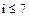, невыполнение которого (i>7) приводит к выходу из цикла.

Следовательно, методом решения является циклический процесс арифметического типа (число повторений 7 – известно) с использованием индекса элементов (i) в качестве параметра.