Глава 1. Математическая формулировка задачи

На примере мостичного амортизатора ставится задача выяснить особенности его состояния при симметричном статическом нагружении вертикальной нагрузкой.

Основные зависимости для арки-полоски

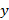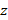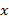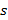Рис. 3. Арка-полоска

Рассмотрим задачу о цилиндрическом изгибе арки-полоски (рис. 3).

Отнесем ее к материальным координатам:

.

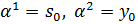Будем считать:

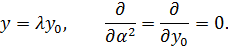
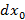Рис. 4

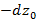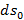Таким образом, рассмматривается одномерная, не зависящая от 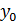, деформация амортизатора, поэтому можно считать его длину (по 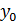единичной). Индексом 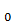снабжаются величины недеформированной конфигурации.

Из рис. 4 видно, что ( :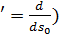

.

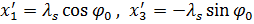Здесь:

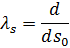
– кратность удлинения дуги в плоскости .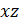

Используется модифицированная геометрическая гипотеза Кирхгофа [3]: материальное волокно, нормальное к материальной срединной поверхности до деформации, остается нормальным к ней и после деформации, удлиняясь по линейному закону.

Для описания упругих свойств эластомеров из несжимаемого материала используется модель трехконстантного потенциала [4]:

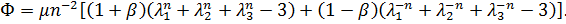
Этому материалу в главных осях деформации отвечает закон упругости:

.

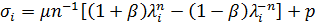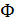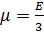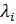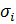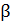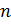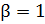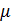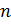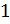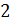Здесь – энергия упругой деформации, – начальный модуль сдвига, где E – модуль Юнга, – главная кратность удлинения, – напряжение, p – сила, обеспечивающая несжимаемость материала, а и – безразмерные константы материала. Далее в работе будет рассматриваться модель двухконстантного материала, то есть . Константы и будут равны и соответственно.

Уравнения равновесия для мостичного амортизатора принимают вид:

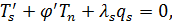
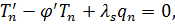
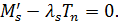
Для изотропно упругого материала определяющие соотношения имеют вид:

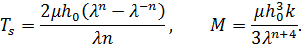
Рис. 5

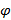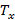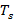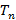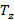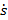Где 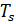– усилие, прикладываемая по касательной к срединой линии в подвижной системе координат, 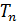– усилие, прикладываемое по нормали к срединой линии в подвижной системе координат, 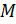– изгибающий момент, 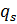и 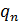– проекции внешней нагрузки в подвижной системе координат.

Перепишем усилия (рис. 5) в проекции на 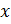и :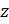

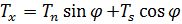
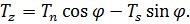
Введя перемещения:

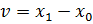
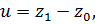
и угол поворота:

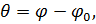
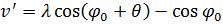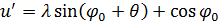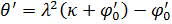	(1.1)

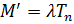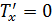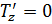составим системы уравнений, описывающие деформацию амортизатора:

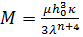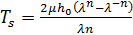	(1.2)

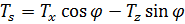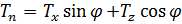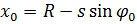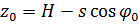	– геометричекие соотношения
.

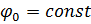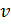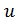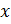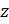Где и – перемещение по осям и соответственно, 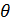– угол поворота, 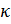– изменение кривизны, 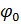и 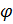– углы между нормалью и осью 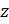до и после деформации соответственно, 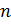– константа материала, 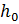– толщина боковой пластины, 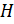– высота амортизатора в недеформированном состояни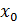и, и 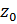– координаты до деформации.

Так как амортизатор представляет собой две симметричные пластины из эластомеров, верхние индексы 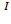и 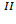будут обозначать левую и правую пластины соответственно. Для определенности 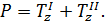Граничные условия для данной задачи будут выглядеть следующим образом:

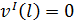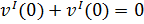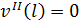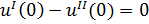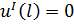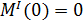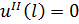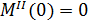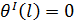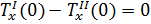		(1.3)
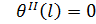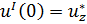		в зависимости от выбора параметра продолжения выбирается одно из этих условий
	,

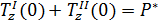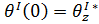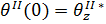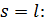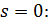где – задаваемое значение.

Решение поставленной задачи

Введем обозначение 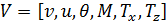для (1.1) и для (1.2). Систему дифференциальных уравнений (1.1) можно представить в виде:

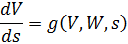(1.4)

а систему (1.2) в виде:

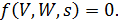(1.5)

Граничные условия (1.3) можно записать в виде:

(1.6)

Задача сводится к решению систем (1.4), (1.5) с граничными условиями (1.6).

Для нахождения точек разветвления решений используется идея метода деидеализации [9]. В данной работе рассматривается два варианта введения неидеальностей:

а) приложение усилия ;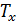

б) фиксированное смещение верхней пластины по оси ,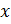

которые ниже будут изложены подробнее.

Алгоритм решения

Задача решается методом стрельбы. Он сводит краевую задачу к задаче Коши. Задача Коши для системы дифференциальных уравнений решается численно методом Рунге – Кутты – Мерсона. Далее методом Ньютона решается система нелинейных уравнений. В качестве начального приближения задается нулевой вектор, так как он является решением для ненагруженного состояния амортизатора. При дальнейшем выборе начальных приближений используетя метод продолжения по параметру. Матрица производных в методе Ньютона считается численно.

Стоит отметить, что, в случае приближения к точке бифуркации, матрицы Якоби становятся плохо обусловленными. В самой точке бифуркации Якобиан принимает нулевое значение, поэтому прохождение по любому из параметров через точку бифуркации становится невозможным.