Расстояние Хэмминга
Для определения того, насколько далеко отстоят друг от друга разные подмножества, существует несколько подходов, задействующих разные метрики. Наиболее распространенным является определение количества мест, в которых отличаются эти упорядоченные подмножества (кортежи, вектора), с учетом того, насколько далеко каждый элемент одного подмножества отстоит от соответствующего элемента другого упорядоченного подмножества. Это и будет расстояние Хэмминга.
Расстояние Хэмминга обозначим
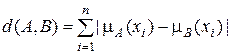 , (1.37)
, (1.37)
где знаки минус и плюс представляет собой операции арифметического вычитания и сложения.
Пример 1.13. Рассмотрим два упорядоченных четких подмножества А и В, принадлежащих множеству Е = {x1, x2, x3, x4, x5, x6, x7}. Пусть A = {x1, x4, x6}, B = {x2, x6, x7}, в иной форме A = {(x1|1), (x2|0), (x3|0), (x4|1), (x5|0), (x6|1), (x7|0)}, B = {(x1|0), (x2|1), (x3|0), (x4|0), (x5|0), (x6|1), (x7|1)}.
Для этих четких подмножеств А и В
d(A, B) = |1– 0| + |0 –1| + |0 – 0| + |1– 0| + |0 – 0| + |1– 1| + |0 –1| = 4.
Более сложные понятия теории нечетких множеств для рассмотрения проблем надежности технических систем и технической диагностики в данном учебном пособии задействованы не будут.
Выводы
Данная глава имеет двоякую цель.
Во-первых, она знакомит читателя с понятием надежности и составными частями надежности, рассматривает виды надежности и формулирует понятие отказа.
Во-вторых, она позволяет читателю освежить в памяти сведения из математики, которые понадобятся для усвоения последующих разделов книги. В главе рассматривается два математических аппарата.
Первый из них – аппарат теории вероятности. Поскольку этот предмет достаточно хорошо знаком каждому инженеру, приводятся только основные сведения, непосредственно используемые в учебном пособии.
Второй – это аппарат теории нечетких множеств. Теория нечетких множеств в последнее десятилетие получает широкое распространение применительно к техническим системам, поэтому авторы сочли необходимым более подробно остановиться на элементах этой теории, сопроводив приводимые понятия комментариями и примерами. В результате читатель из данной главы может получить сведения, необходимые для усвоения материала о теории нечетких множеств, используемого в данном учебном пособии.
Вопросы и задания
1. Сформулируйте определение надежности.
2. Перечислите составные части надежности.
3. Что такое отказ?
4. Какие существуют виды классификации отказов?
5. Одинаковы ли показатели надежности для восстанавливаемых и невосстанавливаемых объектов?
6. Что такое частота случайного события?
7. Чем случайная величина отличается от случайного события?
8. Какие существуют законы распределения для случайной величины?
9. Что показывает математическое ожидание?
10. Что показывает дисперсия?
11. Если значения случайной величины: 8,10,12, то чему равны математическое ожидание и дисперсия?
12. Как определяются надежностные характеристики системы, если известны надежностные характеристики составляющих ее элементов и эти элементы соединены последовательно?
13. Как определяются надежностные характеристики системы, если известны надежностные характеристики составляющих ее элементов и эти элементы соединены параллельно?
14. Является ли корректным следующее представление нечеткого подмножества «небольших» натуральных чисел:
А = {(0|1), (1|0.6), (2|0,7), (3|0,4), (4|0,8), (5|0), (6|0)…}.
15. Какие операции наиболее часто употребляются для четких множеств?
16. Как определяется понятие принадлежности для нечеткого множества?
17. Приведите пример нечеткого подмножества.
18. Как определяется операция «включение» для нечетких множеств?
19. Как определяется операция «пересечение» для нечетких множеств?
20. Как определяется операция «объединение» для нечетких множеств?
21. Какова мера для определения того, насколько далеко отстоят друг от друга разные подмножества?
Список литературы
1. Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М.: Горячая линия-Телеком, 2009. – 608 с.
2. Вентцель Е.С. Теория вероятностей. – М.: КноРус, 2010. – 664 с.
3. Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982. – 432 с.
4. Батыршин И.З. Основные операции нечеткой логики и их обобщения.– Казань: Отечество, 2001. – 100 с.
