Основные свойства 3СЧ, которые необходимо учитывать при построении стеганоалгоритмов

Свойства ЗСЧ можно разделить на две группы: низкоуровневые ("физиологические") и высокоуровневые ("психофизиологические") [75, 76]. Почти до середины 1990-х г.г. исследователи принимали во внимание, главным образом, низкоуровневые свойства зрения. В последние годы обозначилась тенденция построения стеганоалгоритмов с учетом и высокоуровневых характеристик ЗСЧ.

Выделяют три важнейших низкоуровневых свойства, влияющих на заметность постороннего шума в изображении:

• чувствительность к изменению яркости (контрастности) изображения;

• частотная чувствительность;

• эффект маскировки.

На рис. S.2 изображена зависимость минимального контраста 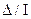от яркости I.

Рис. 5.2. Чувствительность к изменению контраста и порог неразличимости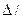

Как видно, для среднего диапазона изменения яркости, контраст приблизительно постоянен, тогда как для малых и больших яркостей значение порога неразличимости 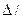возрастает. Установлено, что 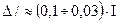для средних значений яркости.

Кроме того, в [5] отмечено, что результаты новейших исследований противоречат "классической" теории и показывают, что при малых значениях яркости порог неразличимости уменьшается, то есть ЗСЧ более чувствительна к шуму в этом диапазоне.

Частотная чувствительность ЗСЧ проявляется в том, что человек намного более восприимчив к низкочастотному (НЧ), чем к высокочастотному (ВЧ) шуму. Это связано с неравномерностью амплитудно-частотной характеристики ЗСЧ.

Элементы ЗСЧ разделяют поступающий видеосигнал, на отдельные составляющие, каждая из которых возбуждает нервные окончания глаза через ряд подканалов. Выделяемые глазом составляющие имеют разные пространственные и частотные характеристики, а также различную пространственную ориентацию (горизонтальную, вертикальную, диагональную) [77].

В случае одновременного влияния на глаз двух составляющих с похожими характеристиками возбуждаются одни и те же подканалы. Это приводит к эффекту маскировки, который заключается в увеличении порога обнаружения зрительного сигнала в присутствии другого сигнала, имеющего аналогичные характеристики. Поэтому, аддитивный шум намного заметней на НЧ (однотонных) участках изображения по сравнению с ВЧ участками, то есть, в последнем случае наблюдается маскировка. Наиболее сильно данный эффект проявляется, когда оба сигнала имеют одинаковую ориентацию и место расположения [5].

Частотная чувствительность тесно связана с яркостью. Известно также и выражение для определения порога маскировки на основе известной яркостной чувствительности, что позволяет найти метрику искажения изображения, которая учитывала бы свойства ЗСЧ. Математические модели такого типа хорошо разработаны для случая квантования коэффициентов дискретного косинусного преобразования, поскольку именно оно применяется в стандарте JPEG.

Эффект маскировки в пространственной области может быть объяснен путем построения стохастических моделей изображения. При этом изображение представляется в виде марковского случайного поля, распределение вероятностей которого описывается, например, обобщенным законом Гаусса.

В [5] предлагается следующая обобщенная схема встраивания данных в изображение:

1. Выполняется фильтрация изображения с помощью ориентированных полосовых фильтров. При этом получается распределение энергии по частотно-пространственным компонентам.

2. Рассчитывается порог маскировки на основе знания локальной величины энергии.

3. Масштабируется значение энергии внедряемой информации в каждом компоненте таким образом, чтобы оно было меньше порога маскировки.

Эта схема так или иначе используется многими алгоритмами встраивания данных.

Высокоуровневые свойства ЗСЧпока еще редко учитываются при построении стеганоалгоритмов [5]. Они отличаются от низкоуровневых тем, что проявляются "вторично" — обработав первичную информацию от ЗСЧ, мозг выдает команды на "подстройку" зрительной системы под изображение.

Перечислим основные из этих свойств:

• чувствительность к контрасту — высококонтрастные участки изображения и перепады яркости обращают на себя больше внимания;

• чувствительность к размеру — большие участки изображения более "заметны" по сравнению с меньшими по размеру, причем существует порог насыщенности, когда дальнейшее увеличение размера не играет роли; '

• чувствительность к форме — длинные и тонкие объекты вызывают больше внимания, чем закругленные и однородные;

• чувствительность к цветам — некоторые цвета (например, красный) более "заметны", чем другие; этот эффект усиливается, если фон заднего плана отличается от цветов фигур на нем;

• чувствительность к месту размещения — человек склонен в первую очередь рассматривать центр изображения; также внимательней рассматриваются фигуры переднего плана, чем заднего;

• чувствительность к внешним раздражителям — движение глаз наблюдателей зависит от конкретной обстановки, от полученных ими перед просмотром или во время его инструкций, дополнительной информации.

В последнее время создано достаточное количество методов скрытия данных в цифровых изображениях, что позволяет провести их классификацию и выделить следующие обобщенные группы [3]:

• методы замены в пространственной области;

• методы скрытия в частотной области изображения;

• широкополосные методы;

• статистические (стохастические) методы;

• методы искажения;

• структурные методы.

Далее рассматриваются особенности, характерные для каждой из выделенных групп. Параллельно приводятся программные модули в системе MathCAD, позволяющие реализовать тот или иной метод, а также промежуточные и конечные результаты соответствующих стеганографических преобразований.

Для каждого модуля даны краткие объяснения относительно его функционирования и использованных функций систем MathCAD. При этом наиболее исчерпывающие объяснения прилагаются к первым рассмотренным методам. В дальнейшем значение функций, содержание которых было раскрыто ранее, не объясняется.

Полное представление о возможностях и правилах использования (синтаксисе) типичных объектов языка MathCAD можно получить, например, из [25, 26]. Кроме того, в данной книге в приложениях А, В, С и D представлена краткая информация относительно встроенных операторов, функций и директив, а также системных переменных и программных операторов системы MathCAD.