Тема 3: Плоскость. Точка и прямая в плоскости
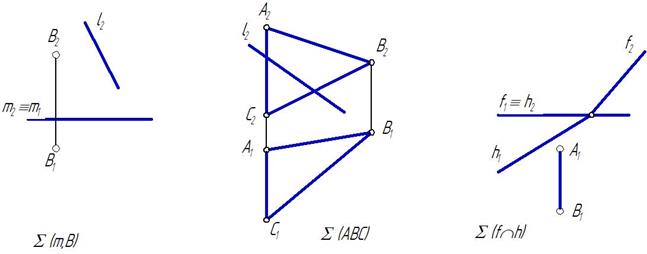
Положение плоскости в пространстве однозначно определяют:
1.____________
2.____________
3.____________
4.____________
5.____________
6.____________
На КЧ плоскость задается проекциями этих геометрических элементов.
След плоскости - _____________________________
_____________.
На след проекций проецируются _________________
_____________
_____________
В зависимости от расположения плоскостей относительно плоскостей проекций они подразделяются на плоскости ____________________.
_____________.
Плоскостью общего положения называются _____
______________
______________.
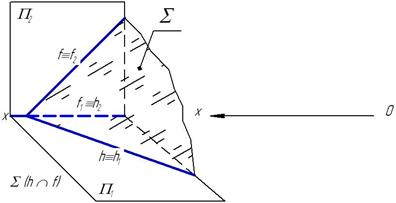
Плоскостями уровня называются _________________
_______________.
К ним относятся:
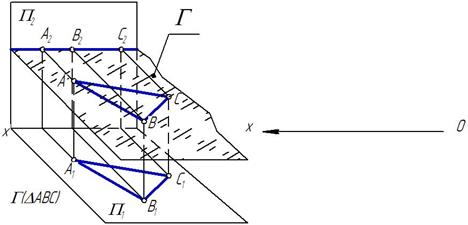
След проекций - ________________________________
_______________
_______________.
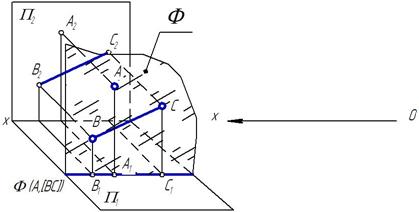
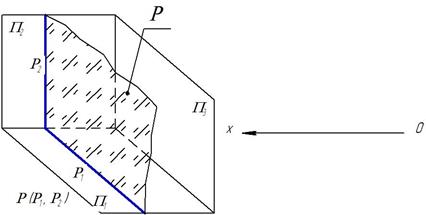
Проецирующими плоскостями называются _________
_______________.
Признаки принадлежности:
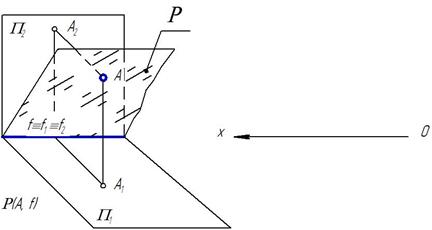
Точка принадлежит плоскости, если ________________
_______________.
Прямая принадлежит плоскости, если ______________
_______________.
Прямая принадлежит плоскости, если ______________
_______________.
Задача 1. Построить недостающие проекции точек, принадлежащих плоскости.

Алгоритм: Алгоритм:
Задача 2. Построить недостающую проекцию прямой линии, принадлежащей плоскости.
Алгоритм: Алгоритм:
Задача 3. Построить произвольную фронталь, принадлежащую плоскости, и горизонталь плоскости, расположенную на расстоянии 40 мм от 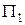 .
.
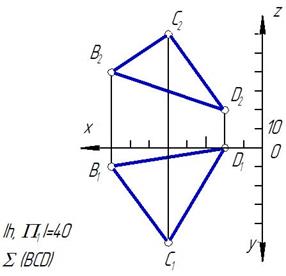
Алгоритм:
Вопросы для самостоятельного контроля знаний
1. Как в пространстве и на КЧ можно задать плоскость?
2. Что называется следом плоскости?
3. Какое положение в пространстве относительно плоскостей проекций может занять плоскость и как при этом она называется?
4. Как по КЧ определить положение плоскости в пространстве, в чем заключается особенность ее задания?
5. Какое свойство имеет плоскость, перпендикулярная плоскости проекций (след проекций)?
6. Как по КЧ установить принадлежность прямой и точки плоскости?
7. Какие линии называются линиями уровня плоскости?
Тема 4: Взаимное расположение плоскостей
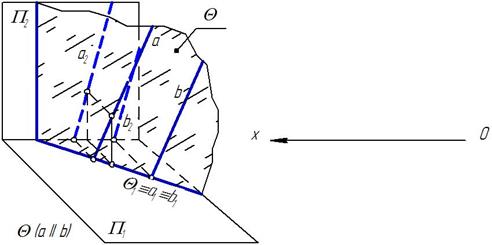
Плоскости могут быть параллельны друг другу или пересекаться.
Признак параллельности:
Плоскости параллельны, если ____________________
_______________
_______________.
| Задача 1. Через точку А провести плоскость, параллельную плоскости S, задав ее линиями уровня. Алгоритм: | 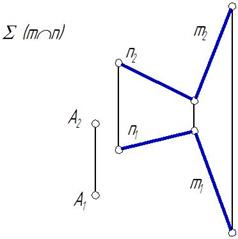 |
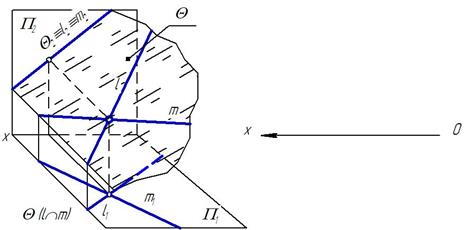
Плоскости пересекаются по ________________.
Эту прямую можно определить, если известны:
1. ____________
______________.
2. ____________
_____________.
Направление линии пересечение известно, если:
1.______________
_______________
_______________.
2.______________
_______________
_______________.
Задача 2-5. Построить линию пересечения плоскостей.
Частные случаи:
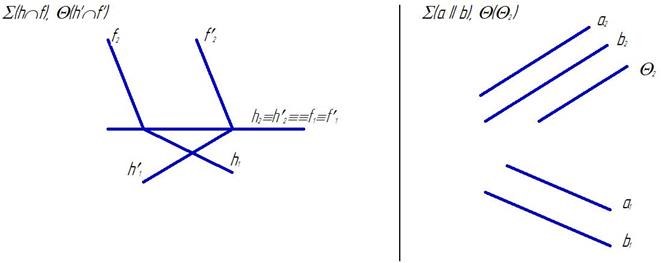
Алгоритм: Алгоритм:
В общем случае линию пересечения плоскостей строят по двум точкам, принадлежащие заданным плоскостям, либо по одной точке, если известно ее направление.
Алгоритм определения общей точки:
1.______________
_______________.
2.______________
_______________.
3.______________
_______________.
Общий случай:
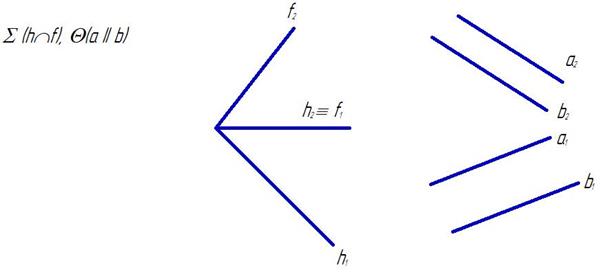
Алгоритм:
Алгоритм:
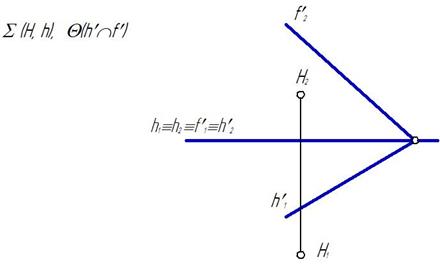
Алгоритм:
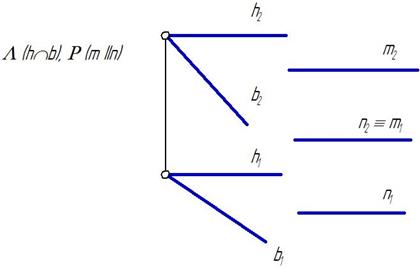
Вопросы для самостоятельного контроля знаний
1. Как формулируется признак параллельности двух плоскостей?
2. Что является результатом пересечения двух плоскостей?
3. Что необходимо определить на КЧ для построения линии пересечения плоскостей?
4. В каком случае известно направление линии пересечения плоскостей?
5. Каков алгоритм построения линии пересечения общем случае?
6. Какую плоскость используют в качестве плоскости-посредника (дополнительной плоскости?
