Точка, прямая, плоскость
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Методические указания и контрольные задания
для студентов механических факультетов
Составители:
доц. Р.Н. Хусаинов
доц. В.В. Сагадеев
Начертательная геометрия. Методические указания и контрольные задания для студентов механических специальностей /Казан. гос. технол. ун-т; Сост.: Р.Н.Хусаинов, В.В.Сагадеев. Казань.
Даны методические указания, задания, алгоритм решения задач, требования к оформлению заданий и примеры выполнения.
Предназначены для студентов механических специальностей, изучающих дисциплину «Начертательная геометрия».
Подготовлены на кафедре инженерной компьютерной графики и автоматизированного проектирования.
Печатаются по решению методической комиссии по циклу общеинженерных дисциплин.
Рецензент: проф. В.А. Лашков
Методические указания, составленные в соответствии с программой дисциплины «Начертательная геометрия», посвящены выполнению эпюра №1 (точка, прямая, плоскость), эпюра №2 (способы преобразования чертежа), эпюра №3 (построение линий пересечения поверхностей и их разверток). Даны варианты индивидуальных заданий, содержание задач, алгоритм их решения, требования по оформлению эпюр и примеры выполнения задач.
Выполнение эпюра – самостоятельная домашняя работа студентов, являющаяся отчетом по пройденной теме.
ЭПЮР № 1
ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ
Цель работы: решение метрических и позиционных задач начертательной геометрии без применения способов преобразования комплексного чертежа.
Объем и оформление работы. Выполнить графическое решение задачи на формате АЗ (297х420) в масштабе 2:1. Координаты точек взять из таблицы 1. Вариант задания соответствует сумме двух последних цифр студенческого билета или зачетной книжки. Чертежи и надписи выполнить соответствии с ГОСТ 2.303-68 (линии) и ГОСТ 2.304-68 (шрифты чертежные). Исходные данные и результат вычертить сплошной основной линией. Линии построения, оси, линии связи, вспомогательные линии – сплошной тонкой линией. Обозначения точек, прямых, плоскостей, алгоритм решения выполнить шрифтом размера 5. В правом верхнем углу поместить таблицу с координатами точек, заполнить ее цифрами шрифтом 7.
Общие сведения. Решение задач эпюра осуществляется на основании следующих положений элементарной и начертательной геометрии.
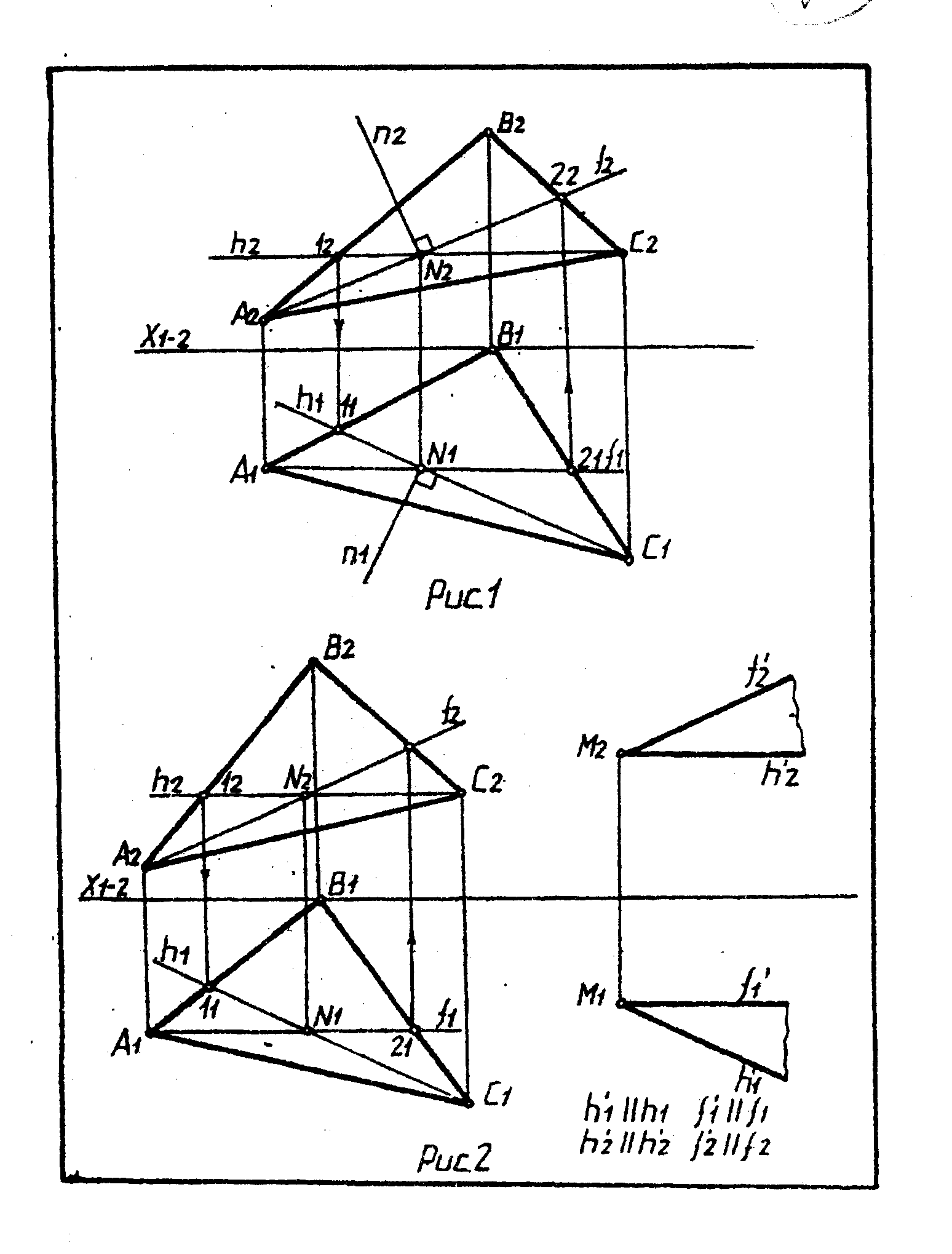
1. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым плоскости. На эпюре проекции перпендикуляра перпендикулярны одноименным проекциям линий уровня n ┴ ∆ ABC, если
n1 ┴ h1, n2 ┴ f2 (рис.l).
2. Две плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. При этом проекции параллельных прямых параллельны(рис.2).
3. Чтобы найти точку пересечения прямой с плоскостью необходимо: а) через прямую провести вспомогательную проецирующую плоскость; б) найти линию пересечения вспомогательной и заданной плоскостей; в) определить искомую точку на пересечении полученной линии и данной прямой (рис.3).
Таблица 1
Координаты точек А, В, С, D в миллиметрах по вариантам заданий
| Точки | № варианта | X | Y | Z | № варианта | X | Y | Z | № варианта | X | Y | Z | № варианта | X | Y | Z |
| А | 1 | 2 | 3 | 4 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 5 | 6 | 7 | 8 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 9 | 10 | 11 | 12 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 13 | 14 | 15 | 16 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 17 | 18 | 19 | 20 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 21 | 22 | 23 | 24 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 25 | 26 | 27 | 28 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D | ||||||||||||||||
| А | 29 | 30 | 31 | 32 | ||||||||||||
| В | ||||||||||||||||
| С | ||||||||||||||||
| D |
4. Для определения величины отрезка способом прямоугольного треугольника необходимо через конец одной из проекций отрезка провести под прямым углом линию и отложить на ней разность координат концов отрезка, взятых с другой проекции. Гипотенуза будет характеризовать величину отрезка (рис.4).
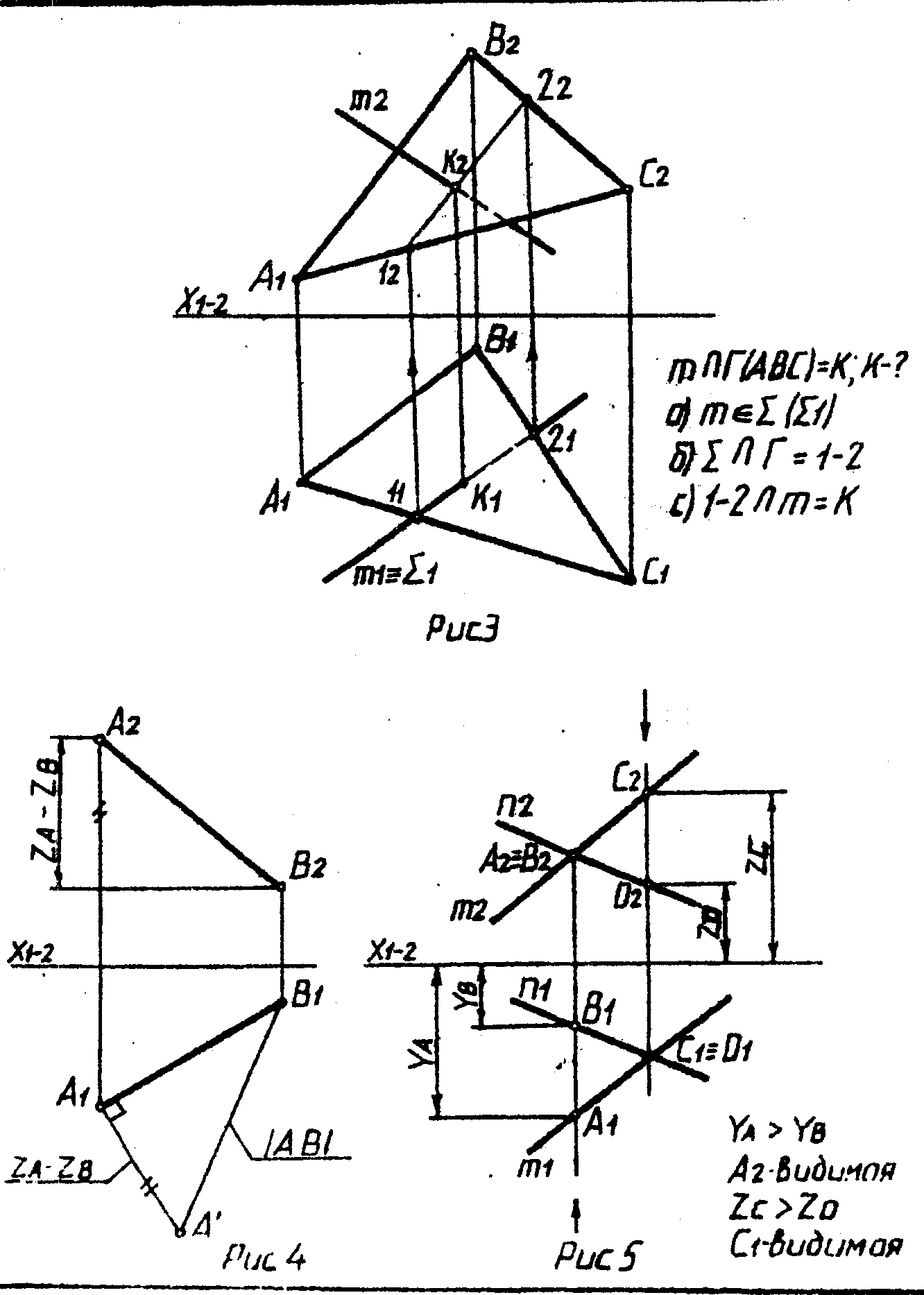
5. Для определения видимости проекций пользуются конкурирующими точками. На горизонтальной плоскости проекций видимой из конкурирующих точек является та, которая имеет большую высоту, т.е. координату Z. На фронтальной плоскости проекций видимой является точка с большей глубиной, т.е. координатой Y (рис.5).
Задача. Определить величину угла между прямой AD и плоскостью треугольника АВС (рис.6).
Приведем поэтапное решение задачи.
Искомый угол φ - это угол между прямой AD и ее проекцией на плоскость треугольникаАВС
1. В треугольнике АВС проведем горизонталь h (h2 h1) и фронталь f (f1, f2). B є h; h2 || OX; A є f; f1 || OX.
2. Из точки пересечения горизонтали и фронтали N (N1, N2) восставим перпендикуляр n (n1, n2) к плоскости треугольника АВС, n ┴ ∆ ABC, если n1 ┴ h1, n2 ┴ f2.
3. Из точки D (D1, D2) проведем прямую m, параллельную перпендикуляру n.
4. Найдем точку пересечения прямой m с плоскостью треугольника АВС. Для этого проведем через прямую m вспомогательную горизонтально проецирующую плоскость Σ (Σ1). Построим линию пересечения плоскости Σ с плоскостью треугольника АВС. Σ ∩ ∆ АВС=3-4. На пересечении линии 3-4 и прямой m получим искомую точку М.
5. Соединим точки A и М - АМ (A1M1• A2M2). Определим величины отрезков АМ и DМ способом прямоугольного треугольника A'М1=|AМ|, D'M1= |DM|.
6. Пострoим по двум катетам АМ и MD (на свободном месте листа А3) прямоугольный треугольник AМD.
Угол DАМ есть искомый угол φ.
7. Определим видимость элементов, используя конкурирующие точки.
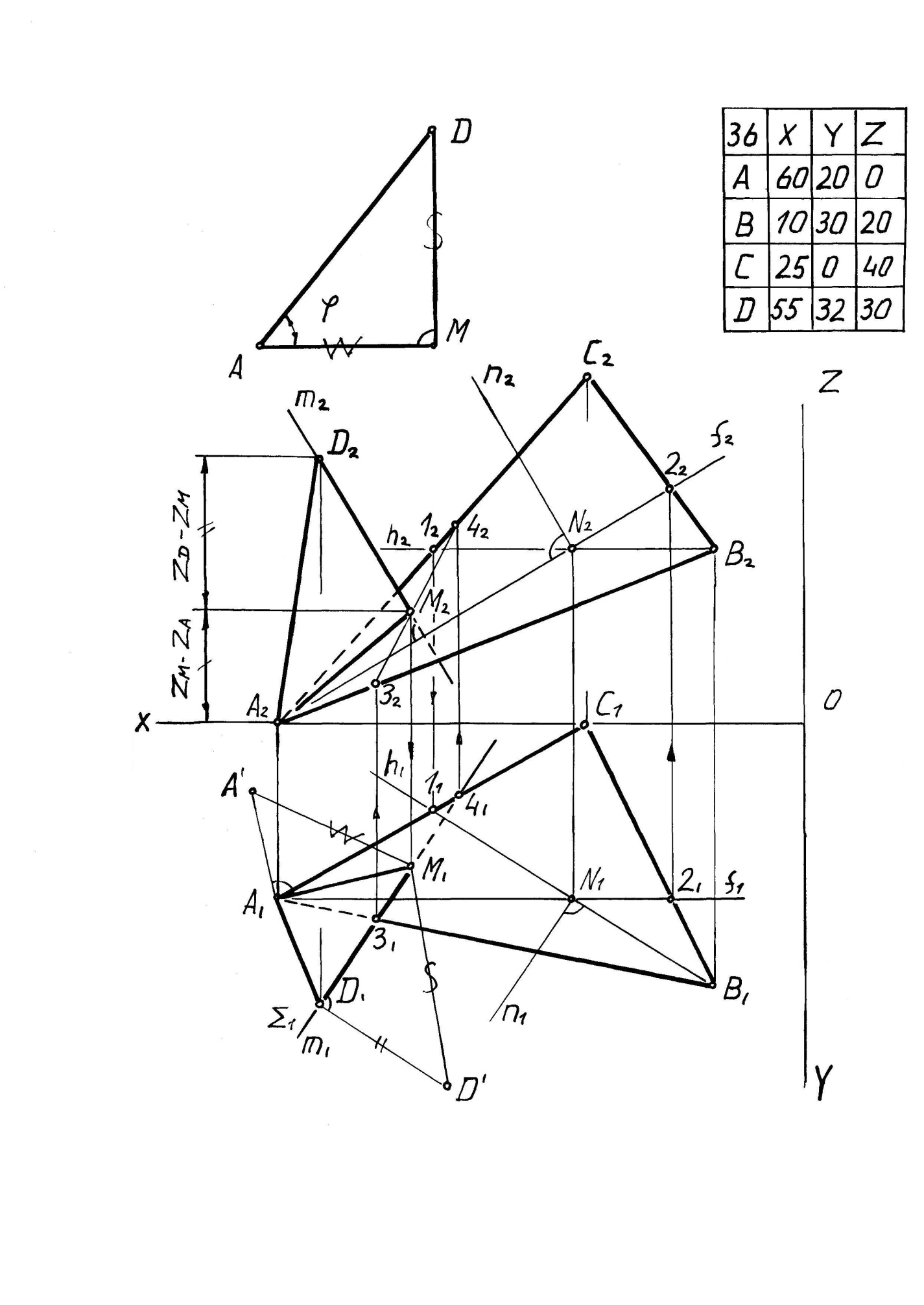
Рис.6.
ЭПЮР №2
