Построение теоретических интегральной и дифференциальной функций распределения.

Если закон распределения изучаемой случайной величины известен или предполагается, то возникает задача построения графиков этого закона применительно к данным полученной статистической выборки. Практически требуется выравнить гистограммы. В частности, выравнивание гистограммы плотности относительных частот дает возможность оценить дифференциальную функцию распределения, а выравнивание гистограммы накопленных относительных частот - теоретический график интегральной функции распределения.

Пусть нам известно, что случайная величина х распределена по нормальному закону. Функция плотности вероятности нормального закона дается выражением:

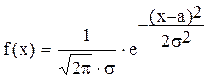(5.1)

где: a - математическое ожидание;

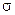- среднеквадратичное отклонение.

Если центрировать случайную величину и нормировать ее на среднеквадратическое отклонение, получится случайная величина:

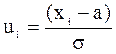
Эта величина распределена также по нормальному закону, но с математическим ожиданием равным нулю и среднеквадратическим отклонением равным единице.

M[u]=0;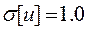

Функция плотности вероятности нормированного нормального закона

(с параметрами M[u] = 0 и 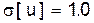) имеет вид:

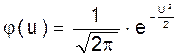(5.2)

и называется функцией Гаусса.

Сравнение формул позволяет выразить функцию плотности вероятности через функцию Гаусса:

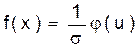
Таким образом, для выравнивания гистограммы плотности относительных частот v_i, т.е. для оценки теоретической функции плотности распределения, необходимо перейти от переменной x к переменной u, заменяя a и 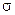их оценками 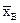и s, а затем воспользоваться формулой

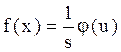(5.3)

где: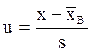

Вероятность попадания нормально распределенной случайной величины х в i-ый интервал равна:

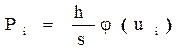(5.4)

где: h - интервал группирования.

Для выравнивания гистограммы накопленных относительных частот вычисления проводятся путем суммирования значения P_i, т.е. накапливая значения вероятности .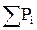

Теоретическую интегральную кривую можно построить и другим способом. С этой целью для правой границы интервала группирования x_j

(где: j = ( 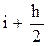)) определяют значение функции F(x_j) по формуле:

F(x_j)=[0.5 +Ф(u_j)] (5.5)

где: Ф(u_j) - интегральная функция Лапласа.

Проведем выравнивание гистограммы рассматриваемого сквозного примера.

При расчетах удобно пользоваться табличной записью:

Таблица 5.1

xi		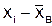ui	j(ui)	f(xi)	Pi=hf(xi)	F(xj)	uj	xj
	-6.04	-2.5	0.0175	0.007	0.004	0.02	-2.1
	-4.04	-1.69	0.0957	0.040	0.080	0.10	-1.26
	-2.04	-0.85	0.2780	0.116	0.232	0.33	-0.43
	-0.04	-0.02	0.3989	0.166	0.332	0.65	0.4
	1.96	0.82	0.2850	0.119	0.237	0.89	1.2
	3.96	1.65	0.1023	0.043	0.085	0.98	2.07
	5.96	2.49	0.0180	0.008	0.015	0.99	2.5

	F(x)
		F(x)
		x
	f(x)

x

Рис.5.1

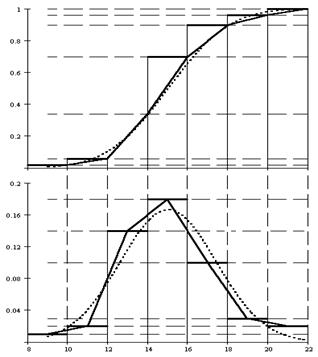
На рисунке 4.1.1 приведены гистограммы 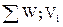и теоретические кривые f_т(x); F_т(x). Оценка математического ожидания рассматриваемой случайной величины (медиана М_е) может быть графически найдена по графику F(x), как абсцисса точки F(x_j) = 0,5.

Вопросы к пятой лабораторной работе

1.В чём смысл работы?

2. Из какого предположения выполняем четвёртую лабораторную работу?

3. Написать формулу нормального закона распределения, построить его график.

4. Как выглядит Закон Гаусса (формула, график).

Лабораторная работа №6.

Проверка гипотезы о нормальном законе распределения.

Критерий Неймана –Пирсона

При изучении геологических процессов и явлений часто приходится проверять гипотезу о том, что выборка распределена по нормальному закону.

Будем пользоваться стратегией Неймана-Пирсона, суть которой состоит в том, что критическая точка определяется при заранее заданном уровне значимости 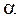. При этом минимизируется ошибка второго рода .

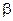В качестве критерия проверки гипотезы о нормальном законе распределения будем использовать критерий Пирсона или .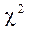

Будем сравнивать эмпирические частоты n_i , взятые из первой лабораторной работы и теоретические 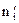частоты, вычисленные по формуле:

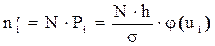(6.1)

Оценку расхождения между теоретической кривой нормального распределения и эмпирической кривой, полученной в результате опыта проводят, по величине отклонения .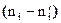

Задача формулируется так: при уровне значимости 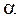требуется проверить нулевую гипотезу H_o о том, что генеральная совокупность распределена по нормальному закону.

Для проверки нулевой гипотезы о нормальном законе распределения рассмотрим случайную величину 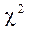, наблюдаемое значение которой вычисляются по формуле:

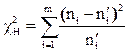(6.2)

Эта величина, как сумма квадратов нормально распределенных величин при 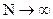, распределена по закону 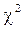с числом степеней свободы: k = m - r - 1,

где:

m- число интервалов группирования .

r- число параметров, определяющих закон распределения. (Для нормального закона r = 2)

Построим критическую область из условия заданной ошибки первого рода (уровень значимости) .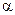

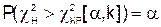
По таблице распределения c² приложение №5 (1) находим 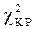и

при 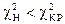делаем вывод о том, что нет оснований отвергать H_o;

при 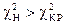- гипотезу H_o отвергаем.

Рассмотрим сквозной пример.

При решении задачи все расчеты запишем в таблицу.

Таблица 6.1

N	xi	ni	n'i=NPi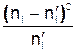
				0.33
			16,0	0.25
			12,0	0.33
				0.2
		N=50	N=50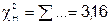

По заданному уровню значимости 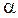=0,05 и числу степеней свободы k = 7-2-1=4 определяем критическое значение 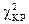. 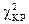= 9,5

Сравнивая 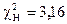c 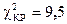делаем вывод:

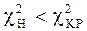, следовательно, нет оснований отвергать нулевую гипотезу H_o.

Таким образом, с надежностью 0.95 можно утверждать, что эмпирические данные не противоречат нормальному закону, т.е. имеющиеся расхождения носят случайный характер.

Вопросы к шестой лабораторной работе.

1.В чём смысл работы?

2. Написать критерий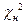

3. Почему, когда 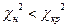– мы говорим нет, основания отвергать нулевую гипотезу?

4.В чём суть стратегии Неймана Пирсона?

5. Дать определение ошибки первого рода и написать формулу.

6. Пояснить смысл полученного результата в пятой лабораторной работе.

8. Можно ли с помощью критерия 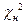проверить гипотезу о другом законе распределения?

Лабораторная работа №7.