Корреляционная зависимость случайных величин. Построение прямой линии регрессии.

Во многих задачах требуется установить и оценить зависимость одной случайной величины Y от другой величины X.

Две случайные величины X и Y могут быть связаны:

1) функциональной зависимостью

2) статистической зависимостью

3) быть независимыми

Определение 7.1:

Статистической зависимостью называется зависимость, при которой изменение одной из случайных величин влечёт изменение распределения другой.

Определение 7.2:

Статистическая зависимость называется

корреляционной если с изменением одной случайной величины меняется среднее арифметическое другой.

1.Вывод уравнения прямой линии регрессии.

Пусть изучается система количественных признаков (X,Y). Предположим, что X и Y связаны линейной корреляционной зависимостью. Найдём по данным наблюдений выборочное уравнение прямой линии регрессии. Искомое уравнение можно записать в виде уравнения прямой линии с угловым коэффициентом:

y=kx+b

Определение 7.3

Угловой коэффициент прямой линии регрессии

Y на X называют выборочным коэффициентом

регрессии Y на X и обозначают r .

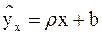( 7.1)

Будем пользоваться методом наименьших квадратов, суть которого состоит в том, что из всех возможных линий на плоскости (из всех возможных значений
r и b) нужно выбрать такие, сумма квадратов отклонений (ε_i)² , которых от линии регрессии была бы наименьшей.

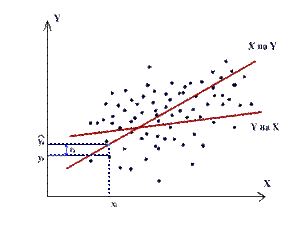
Рис.7.1

Из рисунка видно, что ε_i - отклонение наблюдаемого значения y_i от линии регрессии 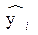. Наша задача – найти такое уравнение, чтобы 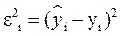( i =1,2,…N), было бы минимальным.

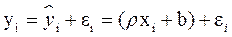
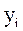–наблюдаемая ордината, соответствующая х_i

Уравнение регрессии Y на X имеет вид:

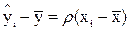
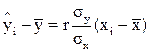(7. 2)

Аналогично запишем уравнение прямой линии регрессии X на Y: 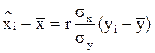(7.3)

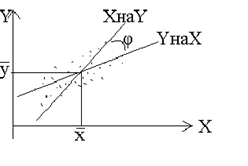Рис. 7..2

Выборочный коэффициент корреляции определяется равенством:

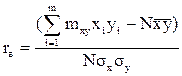(7. 4)

Коэффициент корреляции r изменяется от -1 до 1:

-1 £ r £ 1

Известно, что если величины X и Y независимы, то коэффициент корреляции r = 0; если r = ±1, то X и Y связаны линейной функцианальной зависимостью.

Cледовательно, коэффициент корреляции измеряет силу (тесноту) линейной связи между X и Y.

Выборочный коэффициент корреляции r_в является оценкой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами – количественными признаками X и Y.

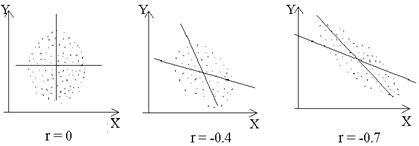
Рассмотрим различные примеры вида корреляционного облака и линий регрессии для некоторых значений r. Они приведены на следующих графиках:

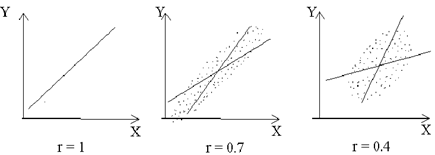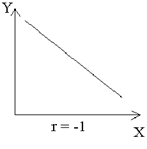Рис.7.3

Пример.

Дана выборка объёмом N = 34

X	Y	X	Y
60.8	5.44	48.4	3.16
58.2	4.13	42.7	3.45
55.4	3.82	52.5	5.28
54.0	0.56	53.2	2.59
44.6	4.61	46.7	1.34
49.5	5.62	37.2	0.69
48.9	0.28	51.4	3.97
35.8	4.10	52.8	3.66
50.6	0.00	43.8	4.30
53.6	0.34	56.0	4.58
44.0	1.15	54.4	3.23
54.3	1.45	51.9	0.15
51.9	2.48	55.1	0.91
41.2	4.70	9.1	1.77
52.5	4.36	8.9	3.40
64.5	5.00	54.4	4.42
51.0	4.19	45.1	3.60

Найти уравнения теоретических линий регрессии Y на X и X на Y и проверить гипотезу о равенстве нулю коэффициента корреляции при уровне значимости 0.05

Решение.

Для решения поставленной задачи составим корреляционную таблицу:

X   Y	8…20	20...32	32...44	44…56	56…68	ny
0…1 0.5
1…2 1.5
2…3 2.5
3…4 3.5
4…5 4.5
5…6 5.5
nx

Для данной выборки вычислим следующие параметры:

1) выборочные средние

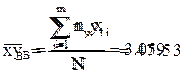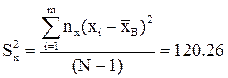2) квадрат стандарта.

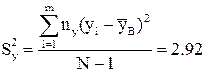Квадрат стандарта является несмещённой оценкой дисперсии , поэтому вместо среднеквадратического отклонения s будем подставлять в формулы корень из квадрата стандарта.

S_х = 10.96 S_y = 1.71

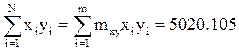Подставим данные коэффициенты в формулу для вычисления выборочного коэффициента корреляции r_в
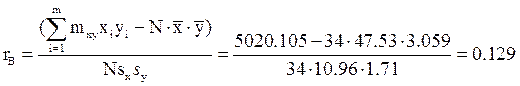