Определение кватернионов и их свойства
Необходимость расширения операций трехмерной векторной алгебры до операций умножения и деления привела Гамильтона (1843 г.) к введению алгебры для четырехмерных чисел, или кватернионов [4, 8]. Под кватернионом понимают число, составленное из действительной единицы 1 и трех мнимых единиц 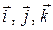 с действительными элементами следующего вида:
с действительными элементами следующего вида:
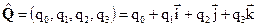 , (1.25)
, (1.25)
где 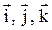 – орты системы координат (мнимые единицы в обозначении Гамильтона). В дальнейшем эти мнимые единицы для удобства изложения будем обозначать, следуя Ганкелю
– орты системы координат (мнимые единицы в обозначении Гамильтона). В дальнейшем эти мнимые единицы для удобства изложения будем обозначать, следуя Ганкелю 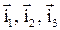 .
.
Существуют разные формы обозначения кватернионов: с кружочком сверху, или готическими полужирными прописными буквами и т.п. В данной работе будем обозначать кватернионы полужирными прописными буквами латинского алфавита с "шапочкой " сверху и с ее выпуклостью к верху.
Изложим основные постулаты, определяющие действия над кватернионами.
1. Два кватерниона 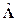 и
и 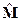 равны, если равны их элементы λi= μi (i=0,1,2,3).
равны, если равны их элементы λi= μi (i=0,1,2,3).
2. Суммой кватернионов 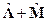 … и
… и 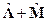 … называется кватернион, элементами которого являются величины λi+μi:
… называется кватернион, элементами которого являются величины λi+μi:
3. 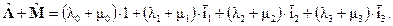
4. При умножении кватерниона 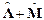 на скаляр а происходит умножение на это число всех его элементов:
на скаляр а происходит умножение на это число всех его элементов: 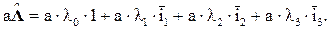
Из этих определений следует, что сложение кватернионов и умножение их на скаляр подчиняется правилам обычной алгебры:

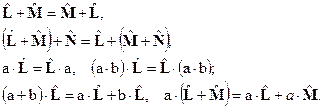 (1.26)
(1.26)
Единицы 1, 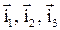 – можно рассматривать как единицы векторы (орты) четырехмерного пространства, которое обозначим Н.
– можно рассматривать как единицы векторы (орты) четырехмерного пространства, которое обозначим Н.
Тогда любой кватернион можно представить в этом пространстве так же, как и в обычном векторном пространстве.
Особенность пространства Н состоит в том, что оно является замкнутым относительно операций умножения и деления.
Чтобы определить правила произведения кватернионов, необходимо задать правила умножения единиц 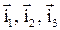 . Эти правила следующие:
. Эти правила следующие:
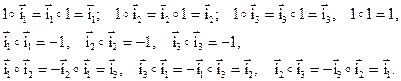 (1.27)
(1.27)
Здесь знак 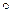 есть символ кватернионного (векторного) умножения.
есть символ кватернионного (векторного) умножения.
При таком правиле умножения произведение двух кватернионов также является кватернионом.
Правила умножения кватернионов удачны – благодаря им алгебра кватернионов содержит в себе алгебру действительных и комплексные числа, а также трехмерную векторную алгебру.
Кватернионы содержат действительные числа (a,0,0,0) с единственной единицей 1, комплексные числа (a,b,0,0) с двумя единицами 1, 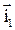 и векторы (0,a,b,c) в пространстве трех измерений. Однако, если действительные и комплексные числа образуют поле (т.е. сложение, умножение и деление дают снова элемент рассматриваемого множества), то произведение двух векторов, как будет показано далее, уже является не вектором, а кватернионом.
и векторы (0,a,b,c) в пространстве трех измерений. Однако, если действительные и комплексные числа образуют поле (т.е. сложение, умножение и деление дают снова элемент рассматриваемого множества), то произведение двух векторов, как будет показано далее, уже является не вектором, а кватернионом.
В соответствии с этим кватернион представим в виде суммы скалярной и векторной частей, которые обозначим sqalQ и vectQ соответственно
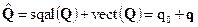 (1.28)
(1.28)
Умножение кватернионов обладает ассоциативными и дистрибутивными по отношению к сложению свойствами.
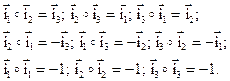 (1.29)
(1.29)
Пусть даны два кватерниона 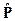 и
и 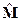 и кватернион
и кватернион 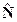 определяется как результат их умножения, т.е.
определяется как результат их умножения, т.е.
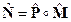 (1.30)
(1.30)
Где
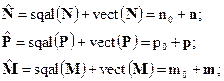
Тогда, учитывая выше сказанное, получим:
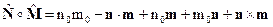 (1.31)
(1.31)
или
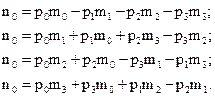 (1.32)
(1.32)
Кватернион, сопряженный данному кватерниону 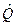 , является следующий кватернион, обозначаемый
, является следующий кватернион, обозначаемый 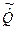 :
:
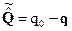 . (1.33)
. (1.33)
Нормой кватерниона называется произведение
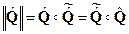 (1.34)
(1.34)
Из формулы умножения следует 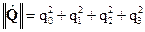 .
. 
Когда норма кватерниона 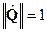 , то кватернион
, то кватернион 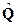 называется нормированным.
называется нормированным.
Нормированный кватернион (в этом случае он называется: кватернион Родрига-Гамильтона)  может быть представлен в виде:
может быть представлен в виде:
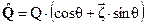 (1.36)
(1.36)
где
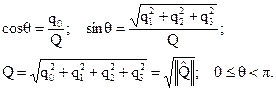 (1.37)
(1.37)
Представление кватерниона в форме (1.46) позволяет получить наглядную геометрическую интерпретацию кватерниона.
В связи с этим кватернион 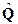 может быть однозначным образом представлен дугой большого круга arc(Q), плоскость которого определяется вектором
может быть однозначным образом представлен дугой большого круга arc(Q), плоскость которого определяется вектором 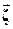 , а длина – углом
, а длина – углом 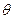 .
.
Направление кватерниона задано направлением вектора 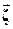 ; т.е. дуга является скользящей (с произвольным началом отсчета).
; т.е. дуга является скользящей (с произвольным началом отсчета).
Заметим, что для нормированного кватерниона сопряженный и обратный кватернион совпадают.
