Материально–техническое обеспечение

1. Установка для лабораторной работы по механике « Определение ускорения свободного падения».

2. Программа для моделирования лабораторной работы на компьютере.

Лабораторная работа №3

«Изучение законов вращательного движения»

Краткая теория

Тело, деформациями которого в условиях данной задачи можно пренебречь, называется абсолютно твёрдым телом. Твердое тело можно рассматривать как систему материальных точек, взаимное расположение которых остаётся неизменным.

Вращательным называют такое движение твердого тела, при котором все его точки движутся в параллельных плоскостях оси вращения и описывают окружности с центрами, лежащими на одной неподвижной прямой , называемой осью вращения (рис.1). При вращательном движении твердого тела все его точки, находящиеся на различных расстояниях от оси вращения, за единицу времени проходят различные пути , следовательно, имеют различные линейные скорости и ускорение .

Для описания кинематики вращательного движения тела нужно задать положение в пространстве оси вращения, угловую скорость и угловое ускорение в любой момент времени. Между угловыми и линейными характеристиками точек вращающегося тела имеется следующая связь

(1)

где r – расстояние данной точки от оси вращения.

Для описания динамики вращательного движения необходимо ввести в рассмотрение ещё две физические величины: момент силы М и момент инерции .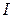

Моментом силы относительно оси 0` (рис.2) называется величина М, определяемая векторным произведением

,

где радиус– вектор, проведённый из точки 0 в точку приложения силы (т.А). Если и лежат в плоскости рисунка, то вектор М расположен перпендикулярно к плоскости рисунка и направлен “от нас ”. На рис. 2 вектор М обозначается кружком с вписанного в него крестиком. Модуль вектора момента силы равен:

(3)

где – угол между направлениями и , а – плечо силы , т.е. длина перпендикуляр из точки 0 на прямую, вдоль которой действует сила . Вращательное движение вызывает только перпендикулярная к составляющая силы . Момент инерции тела относительно некоторой оси – скалярная физическая величина, являющаяся мерой инерции тела при вращательном движении относительно этой оси.

Момент инерции материальной точки, находящейся на расстоянии 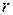от оси вращения, равен

, (4)

где – масса материальной точки. Момент инерции любого твёрдого тела относительно некоторой оси равен сумме моментов инерции всех его элементов (материальных точек) относительно этой оси, т.е.

или (5)

Для тел простейший формы момент инерции сплошного цилиндра, кольца радиуса R и однородного стержня относительно оси проходящей через центр масс этих тел равен соответственно:

; (6)

где ( длина стержня)

В случае, если ось, относительно которой определяется момент инерции , расположена на расстоянии d от оси вращения, проходящей через центр масс тела, и параллельной ей, а момент инерции определяется по теореме Штейнера:

, (7)

где m– масса тела; – момент инерции тела относительно оси, проходящей через центр масс.

При вращательном движении момент силы и момент инерции играют ту же роль, что сила и масса при поступательном движении. Как известно, основным уравнением динамики поступательного движения является II закон Ньютона . Аналогично этому при вращательном движении основное уравнение динамики имеет вид

В данной работе необходимо проверить закономерности при вращательном движении:

1. При постоянном моменте инерции 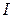системы угловое ускорение пропорционально вращательному моменту М, т.е.

1. При постоянном вращательном моменте силы М угловое ускорение системы e обратно пропорционально моменту инерции J силы, т.е.

Описание установки

Установка представляет собой систему, состоящую из двух шкивов (радиус r₁ и r₂), закреплённых на одной оси 00, и четырёх спиц, на которых закреплены грузы одинаковой массы m₁. Грузы можно перемещать вдоль спиц, закрепляя их на разных расстояниях R от оси. Вся система может приводиться во вращательное движение посредством опускания гири массой m, прикреплённой к шнуру, который намотан на один из шкивов (рис. 3)

Поворачивая всю систему рукой, мы будем наматывать шнур на шкив и тем самым поднимем гирю m на высоту h.

В начале опыта, когда мы удерживаем систему в неподвижном состоянии, а гиря находится наверху, нить натянута силой тяжести этой гири. Но как только мы прекратим удерживать систему, гиря начинает равноускоренно падать с ускорением , где h– высота падения груза, t – время падения. При этом возникает сила . В результате сила натяжения шнура будет равна разности двух сил: где g– ускорение силы тяжести.

Результатирующая сила F приводит во вращение всю систему. Вращательный момент этой силы равен

, (1)

а с учётом основного уравнения динамики вращательного движения (I) и выражения для ε , и получаем:

(2)

где r–расстояние от линии действия силы до оси вращения, 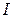– момент инерции системы. Таким образом, измеряя h и t, можно определить a, ε, М и : ;

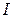; ; , (3)

где =0,007 кг.м² – момент инерции спиц, 4m₁R²– момент инерции четырёх грузов m₁.

Рис. 3