Задание 2: Прямое рассеяние

Измените установку, как показано на рис. 8, используя кольцевую диафрагму из золотой фольги, повернутой глянцевой стороной к источнику.

Рис. 8: Схема установки для изучения рассеивания с использованием фольги кольцевой формы.

Выкачайте воздух из контейнера, закройте детектор от видимого света, откройте программу “Measure”, выберите "Gauge" > "Multi Channel Analyser". Выберите "Integration measurement" («Измерение интеграции»), нажмите "Continue".

В поле "Gain" выберите "Level 2" («Уровень 2»), в "Offset [%]" «Смещение» – 6, а в графе “Recording time [s]” («Время записи (с)») – 1800.

Рис. 9: Окно интегральные измерения

В качестве данных x, введите "distance" («расстояние»), "Symbol" – l, "unit" – cm (рис.9).

Рис. 10: Окно результата измерения.

Установите расстояние между детектором и источником со стержнем, закрепите его крепежным болтом; при помощи магнита закрепите золотую фольгу посередине между детектором и источником.

В качестве исходного значения расстояния выберите 10 см.

Нажмите кнопку “Measure” («Измерить»). Через некоторый промежуток времени на экране появится окно, рис. 10. Введите значение расстояния и нажмите кнопку “Accept value” («Принять значение»).

Измените расстояние , при этом, не передвигая фольгу, и нажмите “Perform measurement” («Выполнить измерение»). Проведите измерения при =5, 7, 10, 14 и 19 см, затем нажмите “Accept data” («Принять данные»).

В основном окне программы выводятся записанные данные. Запишите параметры измерения, используя "Display options" («Опции дисплея») и сохраните данные измерения. Замените золотую фольгу алюминиевой, выкачайте воздух и проведите измерения при = 10 см в течение 2400 с.

Расчет

Рис. 11: Схема установки для резерфордовского рассеивания

На рис. 11: Если принять источник за точку, то поток частиц в фольге определяется как

где - облучаемая площадь фольги, а - активность источника (скорость распада),.

Пространственный угол , в котором рассматриваются частицы, определяется отношением площади чувствительной зоной детектора и квадратом расстояния между фольгой и детектором:

.

При

(2.1)

формула рассеяния (1.12) для установки на рис. 8 имеет вид:

(2.2)

На рис. 8 представлена иная конфигурация, используемая в данном эксперименте. В ней фольга имеет форму кольца с радиусом и располагается посередине между источником и детектором. Другие частицы, не проходящие через фольгу, задерживаются экраном с фольгой, а угол рассеяния зависит от расстояния между источником и детектором, как:

(2.3)

Таким образом, в формуле рассеяния (2.2) следует заменить:

· на , т.к. детектор находится под углом и его проекция по направлению к падению уменьшается;

· на , вследствие увеличения длины пробега для частицы, пересекающей фольгу под углом;

· на , т.к. фольга находится под углом по отношению к частицам и эффективная площадь уменьшается;

· на , где r- длина траектории частицы от источника до детектора.

Учитывая, что

то

,

и формула (2,2) имеет вид

(2.4)

Таким образом, уменьшая расстояние между источником и детектором, увеличится угол рассеяния, и рассеянный поток из-за уменьшится, но поток частиц, ударяющихся о фольгу, увеличивается на , и телесный угол детектора также увеличивается на . Вся конфигурация данной установки компенсирует характер вероятности рассеивания. Согласно (2.4) рассеянный поток частиц не зависит от расстояния между детектором и источником, а зависит от значения . На практике расстояние не должно быть меньше 5 см, поскольку иначе окно детектора закрывает чувствительную зону. Чувствительность детектора S к частицам, достигающим чувствительной зоны, почти равна единице, а скорость счета в темноте равна нулю. "Offset [%]" выбирается так, чтобы частично подавлять регистрацию обладающих малой энергией многократно рассеянных частиц, достигающих детектора, например, при выходе из более глубокого слоя или подвергаясь рассеиванию уже в источнике. Вследствие высокой энергетической чувствительности S целесообразность их учета при расчетах находится под вопросом.

В результате измерений могут получиться подобные результаты:

при

Z (золото) = 79

n (золото) = 5,9·10²² cм^-3

= 4,803·10^-10 СГСЭ

= 3 МэВ = 4,807·10^-6эрг

Значение k, полученное при помощи формулы (2), равно 0,213 см^-1, а при

= 20,16 мм = 2,016 см

= 370 кБк = 2,22·10⁷ мин^-1

= 6 см²

= 1,5 мкм = 1,5·10^-4 см

= 15 мм² = 0,15 см² (при использовании детектора 09099.00)

= 3,1 ·cos мин^-1

Таблица 3: Прямое рассеивание

, см			, экспер., мин-1	, теоретич., мин-1
	90,5		2,2	2,16
	77,8		2,5	2,39
	67,8		2,9	2,55
	53,5		2,9	2,74
	40,3		3,5	2,88
	30,1		3,7	3,0
	21,7		5,0	3,02

На рис. 12 представлен график полученных данных.

Вопросы

Рис. 12: График зависимости рассеянного потока от угла рассеяния (теоретические и экспериментальные значения).

Полученные в ходе измерения данные могут не совпадать с данными, вычисленными по формуле, по трем причинам:

· Предполагаемое значение энергии 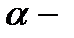частиц = 3 МэВ немного завышено. При распаде Am-241 выделяется = 5,5 МэВ, средняя энергия 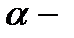частиц источника закрытого типа, использовавшегося в данном эксперименте, составляет около 4 МэВ, но после прохождения золотой фольги толщиной 1,5 мкм ее значение ниже 3 МэВ. При более достоверных подсчетах можно определить значение распределения энергии в каждом слое фольги с вероятностью рассеивания, поскольку предполагаемое значение потока рассеянных частиц обратно пропорционально квадрату энергии 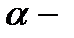частиц.

· Угол рассеяния изменяет толщину фольги, а также энергию частиц вследствие торможения при прохождении через вещество (можно пренебречь). При значениях углов больше 75º или меньше 6 см это приводит к более низким скоростям частиц, которые можно измерить, уменьшив «Смещение», например, до 1%.

· При малых углах или больших l наблюдаются α- частицы, рассеянные электронами атомов, что не учтено в формуле Резерфорда. Об этом свидетельствует значительное увеличение отклонения от теории в диапазоне больших расстояний.

Однако полученные результаты лежат в пределах предполагаемых значений. Кроме этого, видно, что существуют отклонения 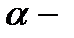частиц высоких энергий на большие углы, что можно объяснить наличием тяжелых частиц в атоме.

Таблица 4: Сравнение результатов рассеивания при = 1,5 мкм, золото (Z = 79) и алюминий - = 8 мкм, (Z = 13) при = 11 см, = 40,3º, n (алюминий) = 6,0·10²²см^-3 и других значениях, указанных выше.

				, экспер., мин-1	, теоретич., мин-1
			8,9·1018	3,5	2,9
			4.8·1019	0,38	0,42

В таблице 4 представлены примеры результатов измерения рассеяния при наличии тяжелых и легких элементов. Из таблицы видно, что результаты рассеяния ниже у элементов с меньшим атомным числом. Поскольку толщина фольги алюминия и плотность частиц на единицу площади больше, то средняя энергия 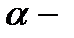частиц меньше по сравнению с энергией для золота. С учетом этого, в ходе эксперимента можно получить более высокое значение результата. Однако энергия рассеянных частиц может быть настолько малой, что некоторые из них остались неучтенными, т.к. значение их энергий было ниже установленного «Смещения». Погрешность вследствие малого числа падений составляет =26%. Однако результаты эксперимента лежат в пределах допустимых значений.

Отчет по работе должен содержать.

29. Цель работы.

30. Краткую теорию.

31. Описание установки согласно рис. 1.

32. Результаты измерений (таблицы).

33. Теоретические расчеты.

34. Сравнение расчетных и экспериментальных данных.

35. Вывод.

Вопросы к отчету

1. Формула Резерфорда.

2. Основные характеристики a- частиц.

3. Взаимодействие a - частиц с веществом.

4. Описание установки.

Литература

1. Техническая документация и методические указания немецкой фирмы PHYWE (на английском языке).

2. Мухин К.Н. Экспериментальная ядерная физика. В 3-х тт. Т. 1. Физика атомного ядра, 2009 Издательство: "Лань", 978-5-8114-0739-2, Год: 2009, 7-е изд, стер.

3. Мухин К.Н. Экспериментальная ядерная физика. В 3-х тт. Т. 2. Физика ядерных реакций, 2009 Издательство: "Лань", ISBN: 978-5-8114-0740-8, Год: 2009, 7-е изд, стер.

4. Мухин К.Н. Экспериментальная ядерная физика. В 3-х тт. Т. 3. Физика элементарных частиц, 2008 Издательство: "Лань", 978-5-8114-0741-5, Год: 2008, 6-е изд., испр.

5. Ракобольская И.В. Ядерная физика. Изд. МГУ, 1981

6. Сивухин Д.В. Общий курс физики, атомная и ядерная физика, ч.2.М.Наука,1989

7. Методические пособия к лабораторным работам по курсу «Физический практикум (Атомная физика)».

ПРИЛОЖЕНИЕ

Физические константы для расчета длин волн линий водорода и дейтерия

π = 3,1415926

c = 2, 99792458*10⁸ м/с

ħ = 1, 05457266*10^-34 Дж*с

1/4πε_о = 8, 9875*10⁹ Н*м²/Кл²

m = 9,1093897*10^-31 кг

е = 1, 60217733 *10^-19 Кл

М_h = 1,6726231*10^-27 кг

М_d = 3, 343615*10^-27 кг

[1] Здесь и далее формулы электродинамики приводятся в таком виде, в котором применяется система единиц в СГС в ее гауссовой форме.

[2] Говоря более строго, гиромагнитное отношение есть величина обратная , однако употребленное название установилось и не вызывает недоразумения.

[3] Резонансным потенциалом атома называется потенциал (в вольтах), численно равный энергии возбуждения атома на соответствующий резонансный уровень.

[4] Мы не учитываем здесь контактной разности потенциалов между электродами лампы, сдвигающей начало отсчета потенциалов, и распределения потенциала вдоль катода.

[5] Функцией возбуждения называется зависимость сечения возбуждения от энергии сталкивающихся частиц.