Неупругие удары второго рода
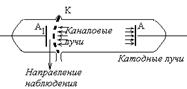 Расщепление уровней энергии атома происходит также во внешнем электрическом поле. Это эффект Штарка(1913). В экспериментах Штарка применялся светящийся пучок каналовых лучей(рис.3.34). Этот пучок через отверстия катода – К разрядной трубки попадал в плоский конденсатор, который состоял из самого катода и вспомогательного анода
Расщепление уровней энергии атома происходит также во внешнем электрическом поле. Это эффект Штарка(1913). В экспериментах Штарка применялся светящийся пучок каналовых лучей(рис.3.34). Этот пучок через отверстия катода – К разрядной трубки попадал в плоский конденсатор, который состоял из самого катода и вспомогательного анода 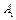 . Расстояние между К и
. Расстояние между К и 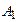 было очень мало – около 1 мм. Поэтому напряженность поля в таком конденсаторе достигала 100 кВ/см.
было очень мало – около 1 мм. Поэтому напряженность поля в таком конденсаторе достигала 100 кВ/см.
рис.3.34. Эффект Штарка наблюдается в любой разрядной трубке в
непосредственной близости от катода, где возникает сильный градиент потенциала. Квантовое объяснение особенностей явления Штарка (Эпштейни Шварцшильд,1916). Дополнительная энергия атома определяется взаимодействием его среднего дипольного электрического момента 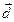 с внешним электрическим полем
с внешним электрическим полем 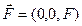 :
:
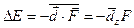 . (3.71)
. (3.71)
В отличие от случая магнитного поля расчет дополнительной энергии атома (3.71) не удается провести точно с помощью простых модельных представлений. Поэтому ограничимся обсуждением простейших результатов последовательных квантово–механических вычислений.
Эффект Штарка существенно зависит от природы дипольного момента атома. Если атом имеет собственный электрический дипольный момент, то дополнительная энергия (3.71) пропорциональна напряженности электрического поля. Это линейный эффект Штарка. Если же атомне обладает собственным дипольным моментом, то во внешнем электрическом поле он приобретает индуцированный дипольный момент, который пропорционален напряженности электрического поля: 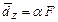 , где
, где 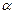 – коэффициент статической поляризуемости атома. Это квадратичный эффект Штарка. Квадратичный эффект проявляется также и для атомов с собственным дипольным моментом. Для большинства атомов эффект Штарка является квадратичным. Исключение составляет атом водорода, а также атомы, находящиеся в сильно возбужденных (водородоподобных) состояниях. Даже сильные внешние электрические поля (исключая лазерные поля) малы по сравнению с внутриатомным электрическим полем порядка
– коэффициент статической поляризуемости атома. Это квадратичный эффект Штарка. Квадратичный эффект проявляется также и для атомов с собственным дипольным моментом. Для большинства атомов эффект Штарка является квадратичным. Исключение составляет атом водорода, а также атомы, находящиеся в сильно возбужденных (водородоподобных) состояниях. Даже сильные внешние электрические поля (исключая лазерные поля) малы по сравнению с внутриатомным электрическим полем порядка 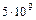 В/cм. Поэтому при расчетах пользуются квантовомеханической теорией возмущений.
В/cм. Поэтому при расчетах пользуются квантовомеханической теорией возмущений.
Эффект Штарка для атома водородав случаесильного электрического поля - штарковское расщепление уровня энергии велико по сравнению с его тонкой структурой. Спин электрона не учитывается. Состояния атома водорода вырождены по орбитальному квантовому числу с кратностью вырождения 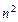 . Существуют состояния, в которых при отсутствии внешнего электрического поля атом водорода имеет собственный дипольный момент. В этом случае распределение зарядов в атоме водорода несимметрично относительно плоскости z = 0, где ось z –выделенное направление внешнего электрического поля. Водородоподобный атом приобретает дополнительную энергию (3.71). Уравнение Шредингера:
. Существуют состояния, в которых при отсутствии внешнего электрического поля атом водорода имеет собственный дипольный момент. В этом случае распределение зарядов в атоме водорода несимметрично относительно плоскости z = 0, где ось z –выделенное направление внешнего электрического поля. Водородоподобный атом приобретает дополнительную энергию (3.71). Уравнение Шредингера: 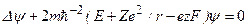 .С помощью параболических координат
.С помощью параболических координат 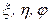 , связанных с декартовыми координатами соотношениями:
, связанных с декартовыми координатами соотношениями: 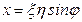 ,
, 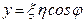 ,
, 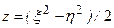 , можно разделить переменные в уравнении Шредингера и использовать теорию возмущений, так что энергия
, можно разделить переменные в уравнении Шредингера и использовать теорию возмущений, так что энергия 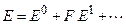 .
.
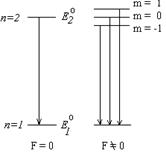 Из решения уравнения Шредингера следует: во внешнем постоянном электрическом поле вырождение уровней энергии атома водорода частично снимается, и уровень энергии с главным квантовым числом n расщепляется на 2n – 1 подуровней. Основной уровень не расщепляется. Первый возбужденный уровень расщепляется на три подуровня (рис.3.35) и т.д. При комбинации 2n –1 компонентов данного терма с 2n’–1 компонентами какого-нибудь другого терма возникают (2n –1)(2n’–1) линий. Например, головная линия лаймановской серии расщепляется на три компоненты, головная линия серии Бальмера
Из решения уравнения Шредингера следует: во внешнем постоянном электрическом поле вырождение уровней энергии атома водорода частично снимается, и уровень энергии с главным квантовым числом n расщепляется на 2n – 1 подуровней. Основной уровень не расщепляется. Первый возбужденный уровень расщепляется на три подуровня (рис.3.35) и т.д. При комбинации 2n –1 компонентов данного терма с 2n’–1 компонентами какого-нибудь другого терма возникают (2n –1)(2n’–1) линий. Например, головная линия лаймановской серии расщепляется на три компоненты, головная линия серии Бальмера 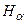 расщепляется на 15 компонент, линия
расщепляется на 15 компонент, линия
Рис.3.35 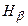 – на 21 компонент и т.д. Линии имеют разную поляризацию: при
– на 21 компонент и т.д. Линии имеют разную поляризацию: при
наблюдении поперек поля линии ( 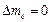 ) поляризованы по полю (
) поляризованы по полю ( 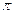 –компоненты), при
–компоненты), при 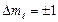 линии поляризованы перпендикулярно полю (
линии поляризованы перпендикулярно полю ( 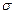 –компоненты). Это соответствует эксперименту. Расстояние между двумя крайними подуровнями:
–компоненты). Это соответствует эксперименту. Расстояние между двумя крайними подуровнями:
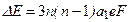 . (3.72)
. (3.72)
Для уровня n = 2 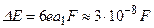 (эВ). При
(эВ). При 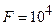 В/см величина расщепления
В/см величина расщепления 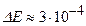 эВ, тогда как разность между уровнями энергии
эВ, тогда как разность между уровнями энергии 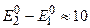 эВ. Увеличение расщепления с возрастанием главного квантового числа можно объяснить тем, что с ростом числа n электрон удаляется от ядра, и, значит, возрастает электрический дипольный момент атома.
эВ. Увеличение расщепления с возрастанием главного квантового числа можно объяснить тем, что с ростом числа n электрон удаляется от ядра, и, значит, возрастает электрический дипольный момент атома.
Общая картина расщепления спектральных линий атома в постоянном электрическом поле довольно сложна, при этом основной задачей является вычисление статических поляризуемостей атомов в различных состояниях.
Во внешнем электрическом поле происходит не только расщепление уровней энергии, но и изменение времени жизни атомных состояний. Например, при помещении атома водорода в электрическое поле 500 В время жизни его метастабильного состояния 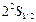 уменьшается на девять порядков. В достаточно сильном электрическом поле может произойти ионизация атома. Эффект Штарка и ионизация атома происходит также во внешнем переменном электромагнитном поле, в частности, в поле лазерного излучения. В монохроматическом поле с частотой
уменьшается на девять порядков. В достаточно сильном электрическом поле может произойти ионизация атома. Эффект Штарка и ионизация атома происходит также во внешнем переменном электромагнитном поле, в частности, в поле лазерного излучения. В монохроматическом поле с частотой 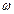 необходимо рассматривать единую систему «атом + поле», которую именуют как «атом, одетый полем». Энергия ионизации «одетого атома» выше, чем потенциал ионизации невозмущенного атома. Волновая функция такой системы есть суперпозиция стационарных состояний с энергиями
необходимо рассматривать единую систему «атом + поле», которую именуют как «атом, одетый полем». Энергия ионизации «одетого атома» выше, чем потенциал ионизации невозмущенного атома. Волновая функция такой системы есть суперпозиция стационарных состояний с энергиями 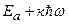 , где
, где 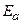 – энергия атома в некотором стационарном состоянии, к – целое число, принимающее значения от -
– энергия атома в некотором стационарном состоянии, к – целое число, принимающее значения от - 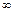 до +
до + 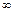 . Существенную роль при этом играет соотношение между частотой поля и частотой перехода в атоме. По этому признаку внешнее поле может быть «низкочастотным» или «высокочастотным». Разделяют также «слабые» и «сильные» поля. Расчет эффекта Штарка в переменном поле является довольно сложным, особенно в случае многоэлектронных атомов.
. Существенную роль при этом играет соотношение между частотой поля и частотой перехода в атоме. По этому признаку внешнее поле может быть «низкочастотным» или «высокочастотным». Разделяют также «слабые» и «сильные» поля. Расчет эффекта Штарка в переменном поле является довольно сложным, особенно в случае многоэлектронных атомов.
Чем больше величина напряженности электрического поля, тем больше вероятность процесса ионизации. Когда напряженность электрического поля F сравнивается с величиной напряженности атомного поля 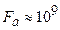 В/см, процесс ионизации происходит за характерное атомное время
В/см, процесс ионизации происходит за характерное атомное время 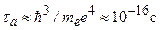 . Cовременная лазерная техника позволяет получать электрические поля, превышающие атомную напряженность. Казалось бы, что в сверхатомных полях
. Cовременная лазерная техника позволяет получать электрические поля, превышающие атомную напряженность. Казалось бы, что в сверхатомных полях 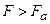 атом не может существовать в связанном состоянии, так как за время
атом не может существовать в связанном состоянии, так как за время 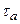 он должен превратиться в ион (или ядро) и свободный электрон. Однако это не так. Электрон может поглотить фотон и оторваться от атома, если только он находится в связанном состоянии в атоме. Поглощение фотона свободным электроном невозможно, так как невозможно одновременно удовлетворить законам сохранения энергии и импульса в системе «электрон + фотон». Таким образом, для поглощения электрон должен быть связанным. Но с увеличением напряженности внешнего поля связь электрона с ядром ослабляется, при
он должен превратиться в ион (или ядро) и свободный электрон. Однако это не так. Электрон может поглотить фотон и оторваться от атома, если только он находится в связанном состоянии в атоме. Поглощение фотона свободным электроном невозможно, так как невозможно одновременно удовлетворить законам сохранения энергии и импульса в системе «электрон + фотон». Таким образом, для поглощения электрон должен быть связанным. Но с увеличением напряженности внешнего поля связь электрона с ядром ослабляется, при 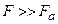 электрон является практически свободным, и поглощение фотонов становится невозможным. Таким образом, вероятность ионизации атома возрастает с увеличением напряженности внешнего электрического поля, пока
электрон является практически свободным, и поглощение фотонов становится невозможным. Таким образом, вероятность ионизации атома возрастает с увеличением напряженности внешнего электрического поля, пока 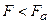 , и уменьшается – при
, и уменьшается – при 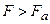 , т.е. максимум вероятности фотоионизации соответствует
, т.е. максимум вероятности фотоионизации соответствует 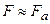 . В сверхатомном поле возникает эффект стабилизации атома по отношению к процессу ионизации
. В сверхатомном поле возникает эффект стабилизации атома по отношению к процессу ионизации
Возбуждение атомов осуществляется многими методами. В частности: возбуждение электронным ударом– при бомбардировке атомов газа направленным пучком электронов, при электрон–атомных столкновениях в газовом разряде; оптическое возбуждение, или оптическая накачка -при воздействии на атом резонансного электромагнитного излучения; термическое возбуждение–при нагревании газа и повышении энергии теплового движения сталкивающихся атомов
Нижние возбужденные состояния атомов условно делятся на резонансно–возбужденныеи метастабильныесостояния. Эти состояния резко отличаются друг от друга по излучательному времени жизни атома (таблица 10).
Таблица 10
| Атом | Метастабиль- ные состояния | Излучательное время жизни (с) | Резонансно- возбужденные состояния | Излучательное время жизни ( 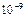 с) с) |
| H | 2 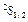 | 0,12 | 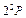 | 1,6 |
| He | 2 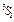 | 2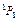 | 0,555 | |
| He | 2 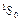 | 0,02 | 3 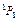 | 1,7 |
| O | 2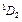 | |||
| Hg | 6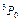 | 1,4 | 6 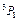 | |
| Hg | 6 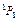 | 1,6 |
Из-за большого времени жизни атомы в метастабильных состояниях накапливаются в газе и влияют на его свойства. Для детектирования метастабильных атомов существуют различные методы. Один из методов основан на измерении поглощения метастабильными атомами резонансного излучения, в результате чего атомы из данного метастабильного состояния переходят в более высокие метастабильные состояния. Так как коэффициент поглощения пропорционален плотности метастабильных атомов, то по измерениям этого коэффициента можно определить искомую среднюю концентрацию метастабильных атомов.
Резонансно-возбужденные атомы освобождаются от избытка энергии как при столкновениях с другими частицами, так и при высвечивании фотонов. Атомы становятся источниками излучения в соответствующем спектральном интервале. На таком принципе работают некоторые газоразрядные источники излучения, например, ртутные лампы.
Когда спонтанное испускание фотона (однофотонный распад) запрещается правилами отбора, то оказывается возможным двухфотонный спонтанный распад.Обычно вероятность двухфотонного распада много меньше вероятности однофотонногораспада.Однофотонный спонтанный (дипольный) переход атома из возбужденного состояния характеризуется временем жизни 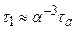 , где
, где 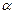 – постоянная тонкой структуры,
– постоянная тонкой структуры, 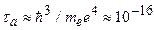 с – характерное атомное время. Для двухфотонных переходов характерное время жизни
с – характерное атомное время. Для двухфотонных переходов характерное время жизни 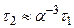 . Например, для атома водорода двухфотонный переход из метастабильного состояния
. Например, для атома водорода двухфотонный переход из метастабильного состояния 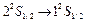 осуществляется за время
осуществляется за время 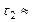 0,15 с.
0,15 с.
Существует также процесс многофотонной ионизации атома. В эксперименте наблюдалась ионизация атома гелия (потенциал ионизации 24,58 В) в результате поглощения 21 фотона излучения неодимового лазера (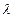 =1,06
=1,06 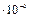 см).
см).
Высоковозбужденные состояния атома - ридберговские состояния:один из электронов внешней оболочки атома имеет большие значения главного квантового числа. Поэтому он слабо связан с остальными электронами и ядром атома. В этом смысле высоковозбужденный (ридберговский) атом аналогичен атомам щелочных металлов. По аналогии с моделью валентного электрона можно считать, что энергия связи электрона (потенциал ионизации) в ридберговском атоме равна 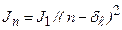 , где
, где 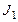 – потенциал ионизации атома водорода,
– потенциал ионизации атома водорода, 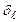 – квантовый дефект, зависящий от орбитального квантового числа
– квантовый дефект, зависящий от орбитального квантового числа 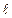 . Параметр
. Параметр 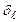 характеризует смещение уровня энергии из-за короткодействующего взаимодействия валентного электрона с атомным остатком. При больших значениях главного квантового числа частота перехода на соседний уровень становится равной классической частоте обращения электрона. Таким образом, ридберговский атом можно рассматривать как диполь, колеблющийся с резонансной частотой, при этом дипольный момент очень велик, так как радиус атома пропорционален
характеризует смещение уровня энергии из-за короткодействующего взаимодействия валентного электрона с атомным остатком. При больших значениях главного квантового числа частота перехода на соседний уровень становится равной классической частоте обращения электрона. Таким образом, ридберговский атом можно рассматривать как диполь, колеблющийся с резонансной частотой, при этом дипольный момент очень велик, так как радиус атома пропорционален 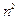 . Для ридберговских атомов атомное электрическое поле зависит от главного квантового числа по закону
. Для ридберговских атомов атомное электрическое поле зависит от главного квантового числа по закону 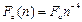 . При больших n такие поля легко реализуются. На свойствах высоковозбужденных атомов основаны современные чувствительные приборы, которые существенно расширяют рамки измерительных возможностей.
. При больших n такие поля легко реализуются. На свойствах высоковозбужденных атомов основаны современные чувствительные приборы, которые существенно расширяют рамки измерительных возможностей.
При поглощении или испускании фотона с импульсом 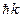 атом испытывает отдачу, скорость которой равна
атом испытывает отдачу, скорость которой равна 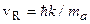 , где
, где 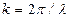 – волновое число излучения,
– волновое число излучения, 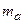 – масса атома. Эта скорость мала. Например, характерная скорость отдачи при оптических переходах в атомах щелочных металлов имеет величину (1–3) см/с. Малой является также энергия отдачи атома
– масса атома. Эта скорость мала. Например, характерная скорость отдачи при оптических переходах в атомах щелочных металлов имеет величину (1–3) см/с. Малой является также энергия отдачи атома 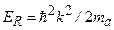 , с которой связывают температуру отдачи одиночного фотона
, с которой связывают температуру отдачи одиночного фотона 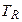 согласно соотношению
согласно соотношению 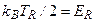 , где
, где 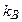 – постоянная Больцмана. Последнее время ведутся теоретические и экспериментальные исследования возможности глубокого охлаждения атомовдо температур, меньших
– постоянная Больцмана. Последнее время ведутся теоретические и экспериментальные исследования возможности глубокого охлаждения атомовдо температур, меньших 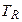 , и удержания их в ограниченном объеме. Первые эксперименты по лазерному охлаждению атомов проводились Летоховым в (1981).
, и удержания их в ограниченном объеме. Первые эксперименты по лазерному охлаждению атомов проводились Летоховым в (1981).
Неупругие столкновения электронов с атомами приводят к потере энергии электронами и возбуждению атомов. Это неупругие удары первого рода. Существует обратный процесс - неупругий удар второго рода:возбужденный атом сталкивается с медленно движущимся электроном. В результате удара второго рода атом без излученияпереходит в основное состояние, а его избыточная энергия передается электрону, который приобретает дополнительную кинетическую энергию. Наиболее вероятными удары второго рода являются в случае возбужденных атомов, находящихся в метастабильном состоянии.
 Удары второго рода происходят также между возбужденныминевозбужденным атомами. Переход энергии возбужденного атома в кинетическую энергию сталкивающихся атомов маловероятный процесс. Наиболее вероятен следующий механизм освобождения энергии возбужденного атома: допустим, что сталкиваются два атома разной природы – А и В. Пусть их возбужденные уровни имеют не сильно различающиеся значения энергии:
Удары второго рода происходят также между возбужденныминевозбужденным атомами. Переход энергии возбужденного атома в кинетическую энергию сталкивающихся атомов маловероятный процесс. Наиболее вероятен следующий механизм освобождения энергии возбужденного атома: допустим, что сталкиваются два атома разной природы – А и В. Пусть их возбужденные уровни имеют не сильно различающиеся значения энергии: 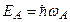 и
и 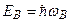 при
при 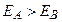 (рис.3.37). Если атом А возбужден, а атом В находится в основном состоянии, то при их столкновении атом А без излучения переходит в основное состояние. Его энергия возбуждения передается атому В, который переходит в возбужденное состояние и затем спонтанно возвращается в основное состояние. При таком переходе испускается фотон с энергией
(рис.3.37). Если атом А возбужден, а атом В находится в основном состоянии, то при их столкновении атом А без излучения переходит в основное состояние. Его энергия возбуждения передается атому В, который переходит в возбужденное состояние и затем спонтанно возвращается в основное состояние. При таком переходе испускается фотон с энергией 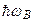 . Это явление сенсибилизированной флуоресценции(Карио, Франк, 1922). Избыток энергии
. Это явление сенсибилизированной флуоресценции(Карио, Франк, 1922). Избыток энергии 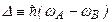 переходит в кинетическую энергию сталкивающихся атомов. Это проявляется в уширении линии излучения вследствие эффекта Доплера. Если возбуждение атома А получено с помощью облучения светом частоты
переходит в кинетическую энергию сталкивающихся атомов. Это проявляется в уширении линии излучения вследствие эффекта Доплера. Если возбуждение атома А получено с помощью облучения светом частоты 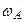 , то в результате ударов второго рода в смеси газов возникает свечение с частотой
, то в результате ударов второго рода в смеси газов возникает свечение с частотой 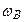 : происходит преобразование коротковолнового излучения в длинноволновое.Этот процесс тем более эффективен, чем меньше разность между уровнями энергии атомов А и В.
: происходит преобразование коротковолнового излучения в длинноволновое.Этот процесс тем более эффективен, чем меньше разность между уровнями энергии атомов А и В.
Сенсибилизированная флюоресценция – не единственный механизм безызлучательного освобождения энергии возбужденным атомом. Существуют процессы, в которых один или оба сталкивающихся медленных атомов находятся в возбужденных состояниях, и в результате образуются ионы и быстрые электроны. Такие процессы - процессы хемоионизации. К ним относятся ионизация Пеннинга и ассоциативная ионизация. Если звездочкой над буквой обозначать атом в возбужденном состоянии, то процесс Пеннинга описывается формулой: 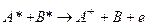 . Образуются атомарный ион
. Образуются атомарный ион 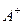 , атом В в основном состоянии и быстрый электрон. В процессе ассоциативной ионизации при столкновении двух возбужденных атомов образуется молекулярный ион
, атом В в основном состоянии и быстрый электрон. В процессе ассоциативной ионизации при столкновении двух возбужденных атомов образуется молекулярный ион 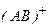 и быстрый электрон:
и быстрый электрон: 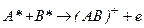 .
.
