Поток вектора напряженности

Электрическое поле можно задать, указав для каждой точки величину и направление вектора 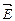. Совокупность этих векторов образует поле вектора напряженности электрического поля. Электрическое поле можно описать с помощью линий напряженности (линий 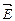), которые проводятся так, чтобы касательная к ним в каждой точке совпадала с направлением вектора 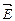. Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, было равно численному значению вектора 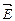. Линии 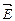точечного заряда представляют собой совокупность радиальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен. Линии одним концом опираются на заряд, другим уходят в бесконечность. Покажем это. Полное число линий N, пересекающих сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на поверхность сферы 4pr². Густота линий по условию численно равна

.

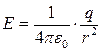Следовательно, N численно равна

,

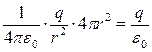т.е. полное число линий на любом расстоянии от заряда будет одно и то же. Следовательно, линии нигде, кроме заряда, не начинаются и не заканчиваются; они, начавшись на заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на заряде.

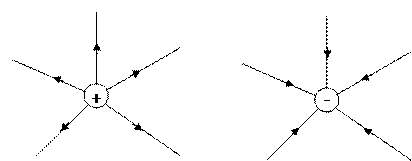
Рис. 13.2.

Поскольку густота линий 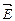выбирается равной численному значению Е, количество линий, пронизывающих площадку dS, перпендикулярных 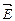будет численно равна ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором 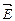угол a, то количество линий, пронизывающих площадку, будет численно равно ЕdS cos a= E_n dS, где E_n – составляющая вектора 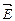по направлению нормали к площадке.

Отсюда для количества линий 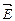, пронизывающих произвольную поверхность, получается следующее выражение:

.

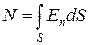Если имеется поле некоторого вектора 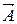, то выражение 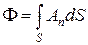, где А_п – составляющая вектора 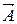по направлению нормали к dS, называется потоком вектора 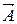через поверхность S.

Следовательно, поток вектора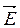

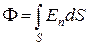(13.7)

численно равен количеству линий 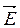, пронизывающих поверхность S.

Теорема Гаусса

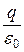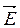В предыдущем разделе было показано, что окружающую точечный заряд qсферическую поверхность любого радиуса r пересекает линий . Отсюда вытекает, что из точечного заряда выходит 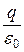линий.

Поток вектора 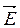через некоторую поверхность численно равен количеству линий 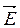, пересекающих эту поверхность. Следовательно, поток вектора 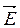через охватывающую заряд сферическую поверхность равен 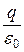. Знак потока совпадает со знаком заряда.

Не сферическая поверхность без «морщин» пересекается каждой линией 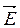только один раз. Поэтому число пересечений равно количеству линий, выходящих из заряда, т.е. .

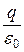Если поверхность с «морщинами», то число пересечений может быть только нечетным и потому противоположные вклады, вносимые в общий поток

Рис. 13.3. взаимно уничтожаются, за

исключением одного.

Таким образом, для любой формы замкнутой поверхности, охватывающей точечный заряд q , поток вектора 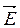сквозь эту поверхность равен .

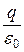Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольный знаков: q₁, q₂ и т.д. Поток вектора 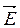по определению равен

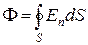(13.8)

(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности).

В силу принципа суперпозиции полей

.

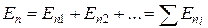Подставив это в выражение для потока, получим

,

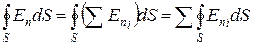где 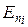- нормальная составляющая напряженности поля, создаваемого і-м зарядом в отдельности.

Но .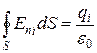

Следовательно 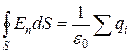. (13.9)

Доказанное утверждение называется теоремой Гаусса. Эта теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀.

Если внутри поверхности заряды отсутствуют, поток равен нулю.

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, теорема Гаусса должна быть записана следующим образом:

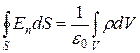, (13.10)

где интеграл справа берется по объему V, охватываемому поверхностью S.

Теорема Гаусса позволяет найти напряженность поля гораздо проще, чем с использованием формулы для напряженности поля точечного заряда и принципа суперпозиции.