Циркуляция магнитного поля
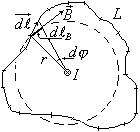 |
Циркуляцией магнитной индукции  вдоль замкнутого контура
вдоль замкнутого контура 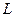 , проведенного в магнитном поле, называется линейный интеграл
, проведенного в магнитном поле, называется линейный интеграл 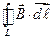 , где
, где  — вектор элементарной длины контура, на которые мы разбиваем контур, направленный вдоль обхода контура,
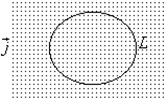
— вектор элементарной длины контура, на которые мы разбиваем контур, направленный вдоль обхода контура,  — индукция магнитного поля в точках малого элемента контура. Проще всего вычислить этот интеграл в случае прямого тока, когда замкнутый контур лежит в плоскости, перпендикулярной к току. На рисунке ток перпендикулярен к плоскости чертежа и направлен за чертеж. В каждой точке контура вектор
— индукция магнитного поля в точках малого элемента контура. Проще всего вычислить этот интеграл в случае прямого тока, когда замкнутый контур лежит в плоскости, перпендикулярной к току. На рисунке ток перпендикулярен к плоскости чертежа и направлен за чертеж. В каждой точке контура вектор  направлен по касательной к окружности (силовой линии), проходящей через эту точку и составляет с током правовинтовую систему. Скалярное произведение векторов
направлен по касательной к окружности (силовой линии), проходящей через эту точку и составляет с током правовинтовую систему. Скалярное произведение векторов  и
и  равно
равно 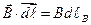 , где
, где 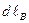 — проекция вектора элемента контура
— проекция вектора элемента контура  на направление поля
на направление поля  . Эта проекция, как видно из рисунка равна длине дуге окружности, являющейся силовой линией магнитного поля
. Эта проекция, как видно из рисунка равна длине дуге окружности, являющейся силовой линией магнитного поля 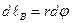 и принимает положительное значение, если направление обхода контура составляет с током правовинтовую систему (направление проекции совпадает с направлением поля
и принимает положительное значение, если направление обхода контура составляет с током правовинтовую систему (направление проекции совпадает с направлением поля  ). Здесь
). Здесь 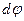 есть угол, на который поворачивается радиальная прямая при перемещении вдоль контура на вектор
есть угол, на который поворачивается радиальная прямая при перемещении вдоль контура на вектор  . В этом случае циркуляция магнитного поля
. В этом случае циркуляция магнитного поля 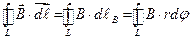 , и учитывая, что индукция магнитного поля, созданного прямолинейным проводником с током бесконечной длины
, и учитывая, что индукция магнитного поля, созданного прямолинейным проводником с током бесконечной длины 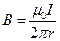 , мы получим
, мы получим 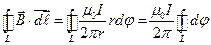 . Интеграл
. Интеграл 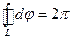 , тогда
, тогда
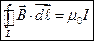 .
.
Если сменить направление интегрирование контура на противоположное, по левовинтовой системе по отношению к току, то в этом случае проекции 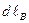 будут принимать отрицательные значения, и
будут принимать отрицательные значения, и
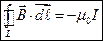 .
.
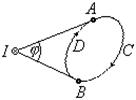 |
Если контур интегрирования не охватывает ток, то циркуляция вектора  равна нулю. Действительно. Разобьем контур на два участка
равна нулю. Действительно. Разобьем контур на два участка 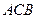 и
и 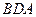 . По участку
. По участку 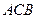 направление интегрирования составляет с током правовинтовую систему, по участку
направление интегрирования составляет с током правовинтовую систему, по участку 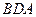 направление интегрирования составляет с током левовинтовую систему. Тогда
направление интегрирования составляет с током левовинтовую систему. Тогда
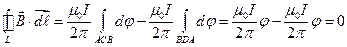 .
.
Рассмотрим циркуляцию магнитного поля, созданного несколькими токами. По принципу суперпозиции полей 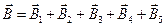 . Тогда
. Тогда
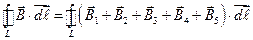 , или
, или
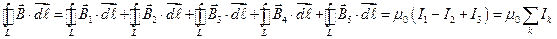 .
.
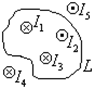 |
Циркуляция индукции магнитного поля равна произведению магнитной постоянной и алгебраической сумме токов, охватываемых контуром интегрирования
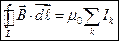 .
.
Ток берется со знаком « 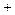 », если он составляет с направлением интегрирования правовинтовую систему, и со знаком «
», если он составляет с направлением интегрирования правовинтовую систему, и со знаком « 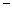 » при левовинтовой системе.
» при левовинтовой системе.
 |
Если контур интегрирования находится в токопроводящей среде, в которой непрерывное распределение тока по площади контура интегрирования задается плотностью тока, то в этом случае сумма токов 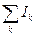 заменяется через интеграл
заменяется через интеграл 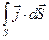 по поверхности S, натянутой на контур интегрирования, а теорема о циркуляции индукции магнитного поля принимает вид
по поверхности S, натянутой на контур интегрирования, а теорема о циркуляции индукции магнитного поля принимает вид
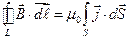 .
.
