Порядок выполнения работы. Вязкость воздуха предлагается определить с помощью прибора

Вязкость воздуха предлагается определить с помощью прибора, представляющего собой U-образный манометр (рис. 2), к одному из колен которого присоединен капилляр К. Если поднять с помощью резиновой груши столб жидкости в одном из колен манометра выше, чем в другом, то в этом случае давление воздуха в колене будет больше атмосферного, и между началом и концом капилляра возникает пере­пад давлений.

Предоставим воздуху возможность вытекать из колена А через капилляр К под действием этого перепада давления. Поскольку воздух имеет вязкость, а капилляр взят тонкий, то уровень жидкости в колене В будет опускать­ся сравнительно медленно. Для определения вязкости будем ис­ходить из формулы Пуазейля (7), откуда

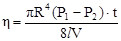, (8)

где V = DhS, но h₁ = h₂ + 2Dh×V = 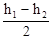×S, Dh = 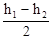. Однако по мере вытекания воздуха перепад давлений будет меняться. Поэтому лучше подставить в формулу Пуазейля средний перепад давления DP_Ср, причем для простоты при небольшом ущербе для точности можно взять среднее арифметическое значение DР: DР_Ср= (DР₀ - DР_t)/2, где DР₀ - перепад давлений в начале отсчета времени, DР_t - перепад давлений в конце отсчета, равный DP_t = (h_2×S×r×g)/2, r - плотность жидкости, g - ускорение силы тяжести. Таким образом, выражение для сред­него давления за время опыта примет такой вид:

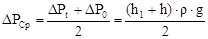. (9)

С учетом этого выражение (8) примет вид:

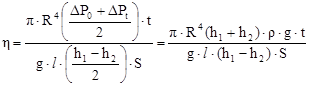. (10)

Таким образом, для экспериментального определения коэффи­циента вязкости нужно измерить:

1) h₁ , h₂ - разность уровней жидкости в манометре в начале и в конце опыта;

2) l - длину капилляра;

3) t - время наблюдения;

4) R - радиус капилляра.

Для измерения диаметров трубки и капилляра используются прилагаемые к установке коротенькие кусочки этого капилляра и этой же трубки. Диаметр капилляра измеряется с помощью микроско­па, диаметр трубки манометра - с помощью компаратора (микрометра). Опыт провести не менее 5 раз. Результаты измерений занести в таблицу.

Таблица

№ опыта	h1, м	h2, м	l, м	t, с	R, м	h, кг/с×м	Примечание
Среднее значение

Подсчитать абсолютную и относительную погрешности в опреде­лении коэффициента вязкости.

Литература

1. Савельев И.В. Курс общей физики. Т. I. - M.: Наука, 1977. § 128, 129, 130.

2. Кикоин А.К., Кикоин И.К. Молекулярная физика. - М.: Наука, 1976. § 35, 36, 48, 49, 50.

3. Грабовский Р.И. Курс физики. - М.: Высшая школа, 1980. § 48-52.

4. Мэрион Дж.Б. Общая физика с биологическими примерами. - М.: Высшая школа, 1986. Гл. 7, 8, 9.

Для получения зачета необходимо

1. Продемонстрировать умение определять коэффициент вязкости воздуха с помощью U-образного манометра.

2. Представить отчет по установленной форме.

3. Уметь отвечать на вопросы типа:

а) Выведите формулу Пуазейля для газов.

б) Почему коэффициент внутреннего трения жидкостей убывает с понижением температуры, а у газов - возрастает?

в) Чем обусловлен знак "минус" в правой части уравнения пе­реноса (внутреннего трения)?

г) Чем обусловлено внутреннее трение в газе?

д) Как зависит от времени сила внутреннего трения в газе?

е) Зависит ли от давления коэффициент вязкости?

ж) Чему равно отношение коэффициента теплопроводности к ко­эффициенту внутреннего трения?

з) Два твердых тела имеют одинаковые размеры и форму, но различны по плотности, сопротивление же воздуха действует на них одинаково. Покажите, что, если, находясь на одинаковой высоте, они освободятся от связей одновременно, то более тяжелое тело достигнет Земли первым.

Дополнительные вопросы для студентов факультетов химии, биологии, института естествознания

1. Известно, что воздух состоит из смеси газов. Дайте характеристику этих газов. Что следует понимать под h?

2. Какое течение называется ламинарным?

3. При чуме артерия сужается и ее эффективный радиус уменьшается на 20%. За счет чего можно понизить давление, чтобы поддержать прежний поток крови?

Работа № 13. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА

Цель работы: экспериментально определить коэффициент вяз­кости неизвестной жидкости, используя метод падающего шарика.

Принадлежности: стеклянный цилиндр на подставке с иссле­дуемой жидкостью, микрометр, набор шариков, пинцет, торсионные весы, масштабная линейка, секундомер.

Вопросы, знание которых обязательно для допуска

к выполнению работы

1. Чем, по представлениям молекулярно-кинетической теории строе­ния вещества, объясняется различие между газом и жидкостью?

2. В чем отличие реальной жидкости от идеальной?

3. Объясните молекулярно-кинетический механизм вязкости.

4. В каких единицах измеряется коэффициент вязкости?

5. От чего зависит коэффициент вязкости?

6. Каким уравнением описывается сила внутреннего трения между слоями жидкости, движущимися с разными скоростями?

7. Сформулируйте законы Стокса и Пуазейля.

8. Применимы ли уравнения переноса, полученные для газа и для жид­кости?

9. Каков физический смысл коэффициента вязкости?

10. Знать порядок выполнения работы.

В в е д е н и е

Рассмотрим механизм возникновения внутреннего трения (вяз­кости) в жидкостях. Молекулы в жидкостях, интенсивно взаимодейст­вуя между собой, находятся на значительно меньших расстояниях относительно друг друга, чем молекулы газа.

Характер теплового (хаотического) движения молекул в жид­костях существенно отличается от теплового движения молекул га­за. Молекулы жидкости большую часть времени колеблются около своего положения равновесия. Вследствие хаотичности движения скорости и амплитуды колебаний соседних молекул различны, и вре­мя от времени соседние молекулы расходятся настолько, что неко­торые из них оказываются на расстояниях порядка диаметра моле­кул (перескакивают) и начинают колебаться около нового положения равновесия.

При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к этим слоям. Это явление называют внутренним трением или вязкостью. Рассмотрим течение вязкой жидкости по горизонтальному руслу. Условно представим жидкость в виде нескольких слоев 1, 2, 3, 4, 5, 6. Слой вязкой жидкости, непос­редственно граничащий с горизонталь­ным руслом, «прилипает» к нему и неподви­жен. По мере удаления от дна скорость слоев жидкости нарастает (v₁<v₂<v₃<v₄<v₅<v₆). Максимальная ско­рость будет у слоя, который граничит с воздухом. Слои воздействуют друг на друга. Более быстрый слой ускоряет соседний с ним более медленный и, наоборот, более медленный задерживает более быстрый.

Вязкость проявляется­ в форме силы, препятствующей относительному движению слоев жидкости, касательной к слоям. Сила внутреннего трения, действующая между двумя слоями, пропорциональна площади соприкосновения взаимодействующих слоев и тем больше, чем больше их относительная скорость. Принято выражать силу в зависимости от изменения скорости, приходящегося на единицу длины в направлении, перпендикулярном скорости, т.е. от величины dv/dy, называемой градиентом скорости (формула Ньютона):

F = h 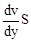. (1)

Величина h называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Если в (1) положить численно dv/dy = 1 и S = 1, то h = F, т.е. коэффициент дина­мической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом ско­рости, равным единице. В системе СИ h измеряется в Па×с. Это такая вязкость, при которой на слой площадью в 1 м² действует сила в 1 Н при градиенте скорости 1 м/с на каждый метр длины.

Из молекулярно-кинетической теории следует, что существование внутреннего трения связано с переносом количества движения молекулами из слоя в слой вследствие теплового движения. В газах перенос количества движения происходит при переходе молекул из одного слоя в другой, что и определяет внутрен­нее трение между слоями. В жидкостях молекулы большую часть времени находятся около положения равновесия и этот меха­низм играет незначительную роль. Основной причиной возникновения сил трения в жидкостях является сильное взаимодействие между молекулами отдельных слоев. Движущийся слой жидкости увлекает соседние слои в основ­ном за счет сил сцепления. Коэффициент вязкости жидкости зави­сит от природы жидкости и от температуры. С ростом тем­пературы коэффициент вязкости жидкости уменьшается (у газов возрастает). Зависи­мость его от температуры жидкости дается формулой Френкеля:

h = B×exp( 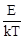), (2)

здесь B - константа, k - постоянная Больцмана, Е - энергия активации: минимальная энергия, необходимая молекуле для преодоления сил взаимодействия с ближайшим окружением и перескока в новое положение равновесия. Величина Е ~ (2-3)*10^-20 Дж, поэтому при нагревании жидкости на 10 градусов вязкость падает на 20-30%. В таблице 1 приведены некоторые характерные значения вязкости.

Таблица 1

Вещество	Температура, оС	h, Па×с
Воздух		1.71 .10-5
		1.84 .10-5
		1.96 .10-5
Вода		1.79 .10-3
		1.00 .10-3
		6.56 .10-4
Глицерин	-42
		1.49
Кровь		4.0 .10-3

Коэффициент вязкости жидкости может быть определен методом падающего шарика в вязкой среде (метод Стокса).

Рассмотрим свободное падение тела (в нашем случае - свинцового шарика) в вязкой покоящейся жидкости, простирающейся безгранично по всем направлениям. На шарик, свободно падающий в такой жидкости, не оставляющий за собой никаких завихрений (это реализуется при малых скоростях падения шариков малых размеров), действуют три силы:

1. Сила тяжести (P):

P = mg = V×r₂ ×g = 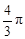r³×r₂×g, (3)

где r - радиус шарика; r₂ - плотность шарика; g- ускорение свободного падения; m - масса шарика; V - объем шарика.

2. Выталкивающая сила(сила Архимеда, F₁):

F₁ = Vr₁g = 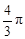r³r₁g, (4)

где r₁ - плотность жидкости.

3. Сила сопротивления движению (F₂, обусловленная силами внут­реннего трения между слоями жидкости):

F₂ = 6 p h r v, (5)

где v - скорость слоев жидкости (скорость шарика).

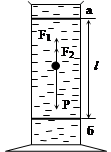
Следует учесть, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, по­скольку при соприкосновении твердого тела с жидкостью к поверх­ности тела сразу же прилипают молекулы жидкости. Тело обволаки­вается слоями жидкости и связано с ними межмолекулярными сила­ми. Непосредственно прилегающий к телу слой жидкости движется вместе с телом со скоростью движения тела. Он увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихре­вое (ламинар­ное) движение (если скорость движения ма­ла и диаметр шариков мал). Направление указанных выше сил по­казано на рис. 2. На основании второ­го закона Ньютона имеем

m 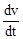= 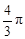r³r₂ g - 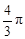r³r₁ g - 6 p hr v . (6)

Вначале шарик падает с ускорением и скорость движения шарика возрастает, но по мере уве­личения скорости шарика сила сопро­тивления F₂ будет также возрастать и, наконец, наступит такой момент, когда сила тяжести Р будет уравновешена суммой F₁ и F₂ и ускорение обратится в ноль:

P = F₁ + F₂. (7)

С этого момента движение шарика становится равномерным с какой-то скоростью v_o.

Подставляя в (7) соответствующие значения для Р, F₁ и F₂, получим для коэффициента вязкости выражение

h = 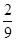(r₂ - r₁) 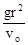. (8)

Формула (8) справедлива, если шарик падает в жидкости, простирающейся безгранично по всем направлениям. Практически невозможно осуществить падение шарика в безграничной среде, так как жидкость всегда находится в каком-то сосуде, имеющем стен­ки и определенную высоту столба. Если шарик падает вдоль оси цилиндрического сосуда радиуса R с высотой жидкости h, то учет наличия стенок и высоты дает следующее выражение для h:

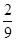
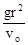
h = 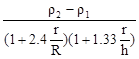. (9)

Вопрос о том, какой формулой пользоваться при расчете, ре­шается в зависимости от величины соотношения r/R и r/h. При движении шарика по оси цилиндра и при соотношении r/R = 1/10 различие в значениях h, полученных по формулам (8) и (9), составляет около 25%.